Статистика и анализ данных
Статистика и анализ данных — это такая область математики, где числа «кричат», то есть играют самую главную роль. Они позволяют нам понять мир вокруг нас благодаря различным количественным характеристикам. Эти данные необходимо особыми способами собрать, организовать, интерпретировать, а после сделать выводы. Для этого существует много методов и инструментов, с которыми мы познакомимся в данной статье.

Все эти концепции нашли широкое применение и в бизнесе, и в медицине, и в социологии. Ведь в наше время, когда данные играют ключевую роль, статистика и анализ информации являются по-настоящему неотъемлемой частью успешной деятельности во многих сферах. Потому что данный раздел математики позволяют выявлять закономерности, аномалии и позволяет делать прогнозы, опираясь на уже имеющиеся сведения.
С чем мы будем работать ?

Конечно же, с числами. Если же быть точнее, то с числовыми рядами.
Это будут не последовательности или прогрессии, а данные, полученные на основе опросов, голосований, результатов исследований, тестирований и тому подобного. Короче говоря, это будут сведения собранные с помощью наблюдения.
Необходимо понимать, что наши вычисления и математические действия не зависят от того чем будет являться наш числовой ряд. Это вообще не важно. Самое главное для нас — научиться использовать методы анализа и статические характеристики.
Элементы статистики.
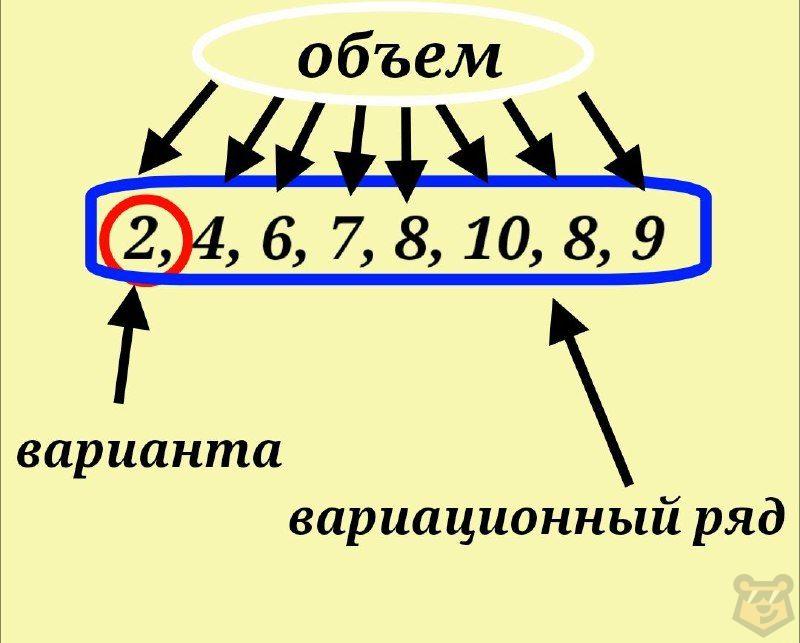
Прежде чем приступить к изучению характеристик, мы должны познакомимся с элементами статики. Они представлены вариационным рядом(выборкой), вариантой и объемом выборки.
Выборка или же по-другому вариационный ряд — это и есть наша полученная информация, если быть точнее, то это совокупность числовых значений.
Пример, {9, 0, 1, 7, 7, 4, 6, 1}. И любые подобные совокупности и множества будут являться выборкой.
Варианта — это любое отдельно взятое число, которое входит в наш ряд. Обычно его обозначают буквой х, у которой есть нижний числовой индекс.
х1 — первая варианта,
х2 — вторая варианта и так далее.
Объем выборки — это количество вариант в нашем множестве, иными словами, это количество всех чисел. Его принято на письме обозначать буквой n.
Рассмотрим простой пример.
Нам дана выборка {3, 6, 7, 6, 7, 8, 3, 3}. Нужно определить ее объем.
Решение. Те, кто подумал, что ответом будет 4, спешу вас огорчить это неправильно.
А вот те, кто получил 8, можете собой гордиться.
Ведь как говорилось ранее, объем состоит из всех элементов ряда. Выходит, что если число у нас повторяется, то мы все равно его должны посчитать. Ведь только так мы найдем правильный объем вариационного ряда.
Даже подумав логически, можно вспомнить, что для того, чтобы найти количество проголосовавших, мы должны считать все листочки с голосами, и не важно встречался или не встречался такой вариант ответа ранее.
Ответ: 8.
Статические характеристики.
Статические характеристики — это такие математические понятия, которые фиксируют и «обрисовывают» наши сведения, наблюдения. Они позволяют нам анализировать нашу информацию и определять ее особенности и характерные черты.
Выделяют 4 основных характеристики.
1) Мода.
Уже только услышав одно название, легко провести аналогию с такими понятиями как «тренд» и «тенденция».
И получается, что модой будет являться самое распространенное и часто встречающееся (самое “модное”) число.
Пример. Вариационный ряд {2, 3, 1, 3, 4, 3, 5, 3}. Найдите моду данной выборки.
Решение. Внимательно смотрим на наше множество чисел и пытаемся определить самое «модное». Замечаем, что чаще всего встречается тройка.
Ответ: 3.
2) Размах.
Делая ассоциации приходим к выводу, что это будет что-то большое, возможно даже огромное. Обратимся к определению и узнаем подтвердятся ли наши предположения.
Размах — это значение разности между максимальной и минимальной вариантой.
Думаю, можно смело заключить, что мы были правы. Ведь чаще всего разность между самым большим значением и самым маленьким действительно велика. Взять ту же минимальную заработную плату, которая не идет ни в какое сравнение даже со средним значением.
Пример. Представлен следующий ряд: {3, 6, 9, 14, 2, 23, 5, 7, 8, 3}. Вычислите его размах.
Решение. Поскольку Размах = max — min, мы должны в начале найти минимальное и максимальное значение.
max = 23, min=2.
Вычисляем разность.
23-2=21
Ответ: 21.
3) Среднее арифметическое.
Вот с данным понятием, мне кажется, многие сталкивались. Поэтому большинству оно возможно знакомо, но для тех, кто не знает этого, объясним.
Среднее арифметическое представляет собой сумму всех вариант ряда, которая поделена на его объем (т.е. на количество всех элементов).
Для того чтобы все лучше понять, разберем один пример.
Ученики в течение двух недель измеряли температуру воздуха и получили следующие данные.
18, 19, 18, 17, 19, 20, 20, 21, 16, 17, 18, 17, 17, 17. Вычислите среднее значение температуры воздуха.
Решение. Получается нам необходимо найти среднее арифметическое данного ряда. Вычисление должно выглядеть примерно так: (x1+x2+…xi)/n.
Из условий самой задачи мы понимаем, что значений было 14, для большей уверенности можете просто посчитать количество полученных чисел.
Теперь найдем сумму всех температур и разделим на количество вариант.
18+18+18+17+19+20+20+20+16+17+18+17+17+17=252
252/14=18
Ответ: 18.
4) Медиана.
Для тех, кто «дружит» с геометрией, сразу же должно быть понятно, что эта характеристика в каком-то плане будет связано с таким понятием как «середина».
Медиана — это число, стоящее посередине нашего множества чисел, которые мы предварительно должны упорядочить, проще говоря записать по убыванию или возрастанию.
Суть медианы заключается в том, что она делит наш ряд на две части, одна из которых меньше медианы, а другая – больше нее. В этом можно убедиться решив, несколько простых задач.
Пример №1. Дан ряд {3, 8, 8, 1, 5, 7, 9}. Найдите медиану.
Решение. Запишем наши значения по порядку. Получим: {1, 3, 5, 7, 8, 8, 9}. В центре, то есть в середине ряда, у нас стоит 7. Это и будет нашей медианой.
Ответ: 7.
Рассмотрим пример №2.
Представлены полученные за 4 четверть оценки по английскому языку {3, 5, 5, 3, 4, 4, 4, 5, 3, 4, 5, 5}. Вычислите медиану ряда.
Решение. Упорядочим нашу выборку.
{3, 3, 3, 4, 4, 4, 4, 5, 5, 5, 5, 5}. Обратим внимание, что объем этого ряда является четным. Потому что n=12. В таком случае медианой будет являться среднее арифметическое двух чисел, стоящих ближе к центру. У нас это 4 и 4. Их среднее арифметическое будет равно 4. Значит медиана равна 4.
Ответ: 4.
Также математиками были выведены специальные формулы для расчета медиан, но ими как показывает практика не очень часто пользуются.
Для нечётного ряда медианой будет являться элементов с номером i=(n+1)/2.
Для четного ряда номер двух чисел для вычисления медианы находят таким образом: i1=n/2 и i2=(n/2)+1.
Мода |  |
Размах |  |
Среднее арифметическое |  |
Медиана |  |
Частоты вариант и полигон частот.
При работе со статистическими данными, мы столкнемся с несколькими видами частот.
1) Абсолютная частота.
Без заумных слов и терминов, абсолютная частота варианты — это такой показатель, который отражает сколько раз в нашем вариационном ряду встречается тот или иной элемент.
Пример. {23, 25, 23, 27, 26, 23, 29} Определим частоту варианты 23.
Решение. Для этого можно сначала упорядочить ряд, а потом просто сосчитать ее количество. Или же можете сразу же приступить к счету.
{23, 23, 23, 25, 26, 27, 29}
Абсолютная частота варианты 23 равна 3.
Ответ: ni=3.
2) Относительная частота.
Относительная частота представляет собою отношение абсолютной частоты варианты к объему выборки: ni/n. Для более продвинутых математиков это, грубо говоря, вероятность данного нам члена ряда.
Пример. {33, 37, 38, 37, 32, 37}. Вычислим относительную частоту варианты 37.
Решение. Найдем объем выборки и частоту этой варианты.
Считаем сколько у нас в ряду чисел, выходит n=6.
Определяем частоту, и получаем 3.
Значит относительная частота равна 3/6=1/2=0,5.
Ответ: 0.5.
Относительную частоту ещё можно представить используя проценты. Ничего сложного в этом нет. Мы должны просто полученное нами отношение умножить на 100%. Получается, при таком раскладе мы пользуемся формулой: ni×100%/n.
Запомните !!!
1) Сумма всех абсолютных частот равна объему выборки.
2) Когда у нас выборка состоит из нескольких разных вариант, то относительная частота одного элемента не должна быть больше единицы или больше ста (в случае, где она представлена в виде процентов).
3) Сумма относительных частот всех вариант всегда должна быть равной либо единице, либо стам.
Благодаря данным свойствам мы можем проверить безошибочность наших вычислений и точность сделанных нами таблиц.
Построение таблицы с абсолютными и относительными частотами.
Такая таблица чаще представлена тремя рядами: вариантa хi, ее частота ni и ее относительная частота ni/n.
Столбцов в таблице будет на 1 больше, чем наших вариант. Почему ? Все просто нам необходим столбец с названиями характеристик.
Самый первый ряд, где у нас представлены наши варианты принято записывать по возрастанию.
Иногда у нас добавляется четвертый ряд, но только в том случае, где в самом задании требуют представить относительную частоту и в виде дроби, и в виде процентов.
Предлагаю для наглядности и простоты понимания составить одну такую таблицу.
Результаты 11 класса по профильным предметам на ЕНТ представлены следующим рядом: 40, 38, 39, 49, 46, 21, 39, 40, 21, 14. Составьте на основе этих данных таблицу абсолютных и относительных частот в дробях, в процентах.
Решение. Упорядочим наш ряд: 14, 21, 21, 38, 39, 39, 40, 40, 46, 49.
Получается, что всего наших вариант 7, а объем данной выборки n=10.
Это значит, что количество столбцов у нас будет 8 (7+1). Теперь составим таблицу.
| варианта | 14 | 21 | 38 | 39 | 40 | 46 | 49 |
| абс. ч-та | |||||||
| относ. ч-та | |||||||
| относ. ч-та % |
Сейчас будем определять сколько учеников набрало каждый балл, то есть сколько раз каждая из данных вариант встречается в этой выборке (абсолютная частота).
14 — 1 р.
21 — 2 р.
38 — 1 р.
39 — 2 р.
40 — 2 р.
46 — 1 р.
49 — 1 р.
Переносим наши вычисления в таблицу.
| варианта | 14 | 21 | 38 | 39 | 40 | 46 | 49 |
| абс. ч-та | 1 | 2 | 1 | 2 | 2 | 1 | 1 |
| относ. ч-та | |||||||
| относ. ч-та % |
Теперь определяем по формуле ni/n относительную частоту каждого элемента, которая будет представлена дробью.
14 — 1/10=0,1
21 — 2/10=0,2
38 — 1/10=0,1
39 — 2/10=0,2
40 — 2/10=0,2
46 — 1/10=0,1
49 — 1/10=0,1
Вносим наши данные в таблицу.
| варианта | 14 | 21 | 38 | 39 | 40 | 46 | 49 |
| абс. ч-та | 1 | 2 | 1 | 2 | 2 | 1 | 1 |
| относ. ч-та | 0,1 | 0,2 | 0,1 | 0,2 | 0,2 | 0,1 | 0,1 |
| относ. ч-та % |
Сейчас вычисляем относительные частоты в процентах.
14 — 0,1×100=10%
21 — 0,2×100=20%
38 — 0,1×100=10%
39 — 0,2×100=20%
40 — 0,2×100=20%
46 — 0,1×100=10%
49 — 0,1×100=10%
Заполняем таблицу.
| варианта | 14 | 21 | 38 | 39 | 40 | 46 | 49 |
| абс. ч-та | 1 | 2 | 1 | 2 | 2 | 1 | 1 |
| относ. ч-та | 0,1 | 0,2 | 0,1 | 0,2 | 0,2 | 0,1 | 0,1 |
| относ. ч-та % | 10% | 20% | 10% | 20% | 20% | 10% | 10% |
Естественно, такие лёгкие вычисления мы в основном будем делать либо в уме, либо на черновике. Сейчас все подробно написали для того, чтобы лучше уловить суть и что за чем следует.
3) Накопленная частота и таблицы с ней.
Накопленная частота — это сумма абсолютных частот всех предшествующих столбцов.
То есть накопленная частота варианты х1 будет равна ее абсолютной частоте n1, накопленная частота элемента х2 будет равна сумме n1+n2, накопленная частота числа х3 будет равна сумме n1+n2+n3 и так далее.
Рассмотрим алгоритм нахождения накопленных частот с помощью прошлой таблицы. Возьмем от нее лишь два ряда.
| варианта | 14 | 21 | 38 | 39 | 40 | 46 | 49 |
| абс. ч-та | 1 | 2 | 1 | 2 | 2 | 1 | 1 |
Делаем вычисления следующим образом:
14) 1+0=1
21) 2+1=3
38) 3+1=4
39) 4+2=6
40) 6+2=8
46) 8+1=9
49) 9+1=10
Переносим наши значения в таблицу.
| варианта | 14 | 21 | 38 | 39 | 40 | 46 | 49 |
| абс. ч-та | 1 | 2 | 1 | 2 | 2 | 1 | 1 |
| накоп. ч-та | 1 | 3 | 4 | 6 | 8 | 9 | 10 |
Полигон частот.
Полигон частот является графическим отражением всех вариант ряда и только одной из трех их частот.
Построение полигона не зависит от такого с каким видом частоты мы будем работать. При выполнении задания и с абсолютной, и с относительной, и с накопленной частотой нужно пользоваться одним и тем же алгоритмом.
1) Чертим I четверть координатной плоскости.
Потому что именно здесь наши обе оси положительны, а это важно ведь наши частоты не могут быть со знаком минус.
2) По оси абсцисс отметим наши варианты.
3) По оси ординат расположим данную нам частоту.
4) Отмечаем точки, координаты которых будут представлены вариантой хi по х, и нашей частотой по у.
5) С помощью линейки соединяем все точки таким образом, чтобы получить ломаную линию.
Построим полигон абсолютной частоты, используя данный принцип.
Сколько человек какую оценку получили за СОР учитель представил в следующей таблице. На основе данных сведений составьте полигон абсолютных частот этой выборки.
| варианта | 2 | 3 | 4 | 5 |
| абс. ч-та | 2 | 5 | 3 | 4 |
Действуем по алгоритму. Чертим часть координатной плоскости, где отмечаем наши данные.
Теперь найдем точки, чьи координаты строятся по принципу (хi;ni).
В итоге опираясь на таблицу мы получим: (2;2), (3;5), (4;3), (5;4).
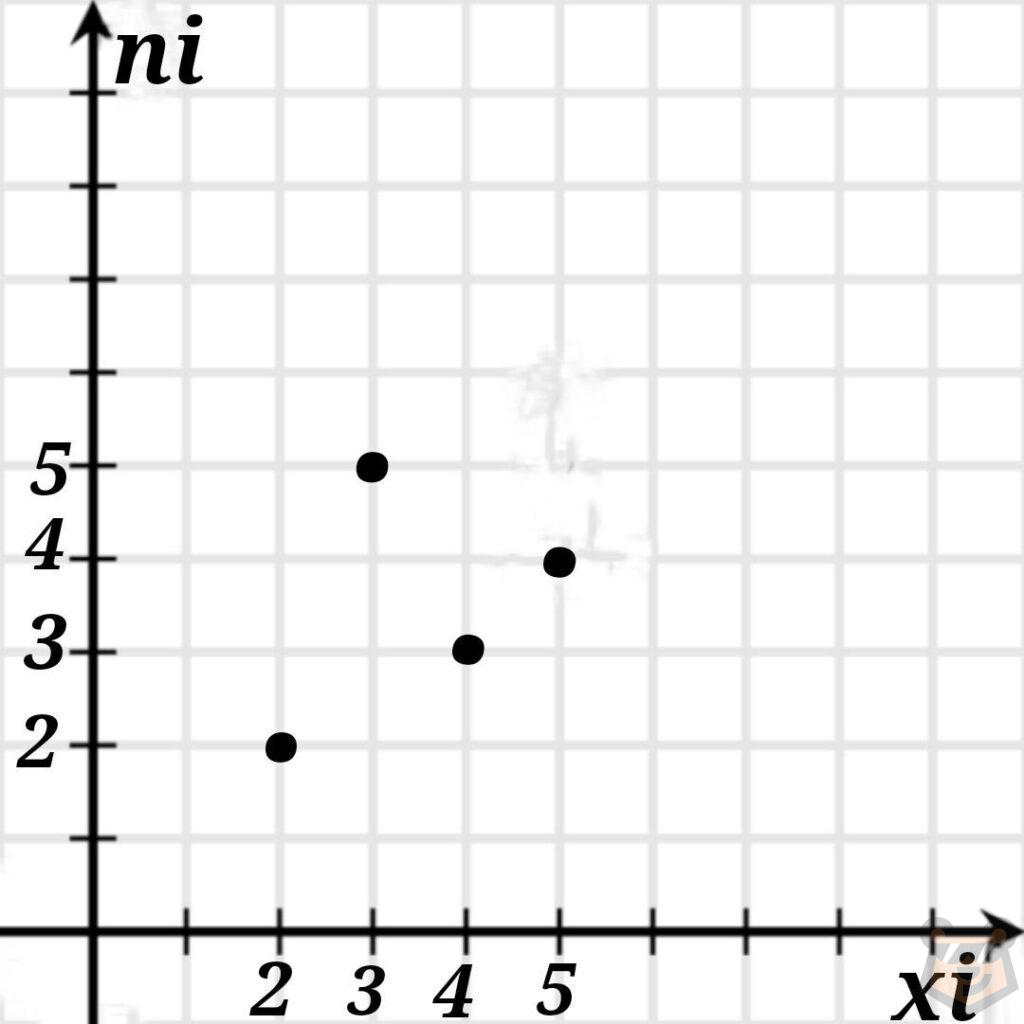
После этого соединяем наши точки.
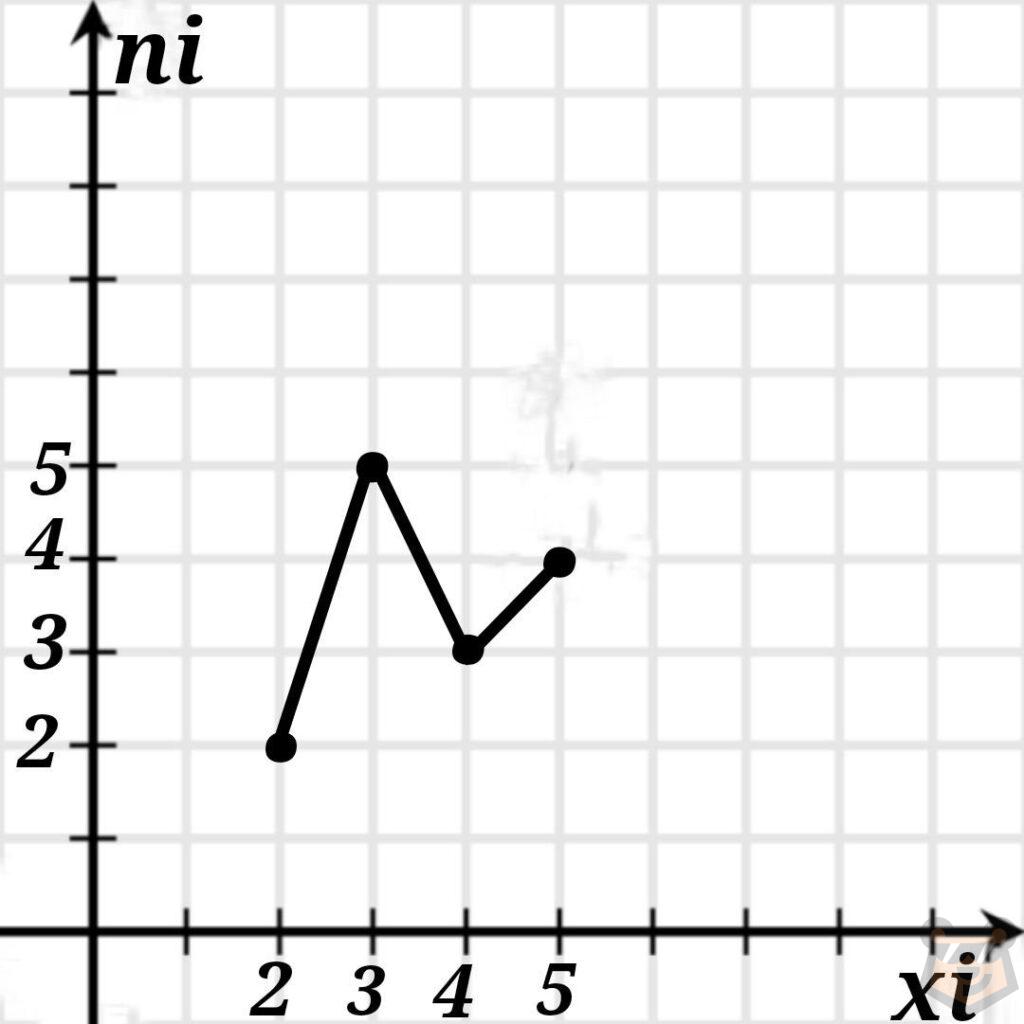
Точно так же мы должны строить полигоны с относительными и накопленными частотами.
Виды вариационных рядов.
В зависимости от типа вариации (то есть метода по которому распределяются наши варианты) можно выделить несколько видов вариационных рядов.
1) Дискретный ряд.
Варианты такой выборки представлены одним целым числом. Выходит, что все прошлые задания и таблицы, которые мы выполняли, являются примером дискретного ряда.
2) Интервальный ряд.
Конечно же, основой такой вариации будут интервалы, включающие в себя сразу несколько чисел. Получается, наши так называемые варианты выборки при таком раскладе являются не одним конкретным значением, а промежутками, построенными по типу “от и до”.
Рассмотрим один пример.
В армии провели взвешивание для новоприбывших и получили следующие результаты.
| варианта | [65-70) | [70-75) | [75-80) | [80-85) | [85-90) | [90-95] |
| абс. ч-та | 2 | 4 | 3 | 16 | 8 | 5 |
Значит, смотря на такой ряд, мы не сможем сказать точно сколько человек весит 61 кг или 89 кг, но мы легко узнаем сколько человек входит в определенную весовую категорию.
Для индивидуальных рядов существует две формулы.
1)![]()
Такое выражение позволяет определять количество промежутков.
2) ![]()
Эта формула дает нам возможность вычислить длину интервала.
k — кол-во вариант (интервалов)
i — длина интервала (то самое “от и до”)
Научимся ими пользоваться на примере прошлого задания.
Случай №1. Нам известно, что самый большой зафиксированный вес — это 95 кг, а самый маленький — 65 кг. Нам необходимо определить сколько столбцов с данными взвешивания нужно заполнить, если длина интервала равна 5.
Решение. xmax=95, xmin=65, i=5. Используем подходящую формулу.
k = (95-65)/5 = 30/5 = 6.
Ответ: 6.
Случай №2. Самым большим зафиксированным весов среди новичков был — 95 кг, а самым маленьким — 65 кг. Вычислите длину интервала, учитывая то, что всего вышло 6 вариант.
Решение. xmax=95, xmin=65, k=6. Расчеты делаем, опираясь на нужную формулу.
i = (95-65)/6 = 30/6 = 5.
Ответ: 5.
Смежные понятия с теорией вероятности.
Некоторые элементы математической статистики тесно связаны с вероятностями. Поэтому для того, чтобы приступить к изучению следующих явлений, прежде всего необходимо ознакомиться с теорией вероятности.
1) Математическое ожидание.
Математическое ожидание — это среднее значение величины, которую мы можем получить случайным образом.
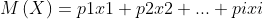
Обратив внимание на формулу, можно понять, что для нахождения данной величины нам необходимо каждую варианты умножить на ее вероятность (т.е. на относительную частоту) и сложить все полученные значения.
Вернемся к одному уже ранее выполненному заданию.
| варианта | 14 | 21 | 38 | 39 | 40 | 46 | 49 |
| относ. ч-та / вероятность | 0,1 | 0,2 | 0,1 | 0,2 | 0,2 | 0,1 | 0,1 |
М(Х) = (14×0,1)+(21×0,2)+(38×0,1)+(39×0,2)+(40×0,2)+(46×0,1)+(49×0,1) = 1,4 + 4,2 + 3,8 + 7,8 + 8 + 4,6 + 4,9 = 34,7
2) Дисперсия.
Дисперсия — это такая величина в статистике, которая отражает разброс (отличие) полученных наблюдений относительно математического ожидания.
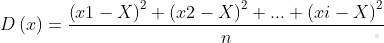
В этом выражении:
Х — среднее арифметическое всех вариант,
n — кол-во элементов,
хi — варианты.
Обычно запись (хi-x)^2 принята называть квадратом среднего отклонения.
Запомним материал с помощью одного задания.
Дан числовой ряд: 4, 9, 1, 5, 3, 2. Вычислим его дисперсию.
Решение. Во-первых, найдем объем выборки. n = 6
Во-вторых, вычислим среднее арифметическое. Х=х1+х2+…хi/n
Х = (4 + 9+ 1+ 5 + 3+ 2)/6 = 4
В-третьих, подставляем в нашу формулу получены вычисления и находим дисперсию.
D = ( (4-4)^2 + (9-4)^2 + + (1-4)^2 (5-4)^2 + (3-4)^2 + (2-4)^2 ) / 6 = ( (0)^2 + (5)^2 + (-3)^2 + (1)^2 + (-1)^2 + (2)^2 ) / 6 = (0 + 25 + 9 + 1 + 1 + 4) / 6= 40 / 6 = 6.7
Ответ: 6.7.
3) Среднее квадратичное отклонение.
Среднее квадратичное отклонение это величина, характеризующая среднюю степень различия между вариантами относительно математического ожидания.

Формула очень простая. Необходимо только вычислить корень из дисперсии.
Например, среднее квадратичное отклонение прошлого ряда согласно формуле будет равно √6.7 = 2.59.
| Дисперсия. | Среднее квадратичное отклонение. |
 |  |

Практическая работа.
Задание №1. Учёные при сборе нового сорта картофеля произвели взвешивание. Результаты массы отражены в следующем ряду:
46, 50, 55, 48, 46, 53, 46, 55, 48, 55, 51, 55.
А) На основе этих данных составить таблицу с абсолютной, относительной и накопленной частотами. Представьте относительную частоту и с помощью дробей и с помощью процентов.
В) Составьте полигон абсолютных частот.
Решение. Упорядочим наши числа. 46, 46, 46, 48, 48, 50, 51, 53, 55, 55, 55, 55.
Всего у нас 6 элементов: 46, 48, 50, 51, 53, 55. (1 ряд) Значит чертим 7 столбцов.
Определим сколько раз у нас встречается каждое из чисел.
46 — 3 р. ; 48 — 2 р. ; 50 — 1 р. , 51 — 1 р. ; 53 — 1 р. ; 55 — 4 р. ( 2 ряд)
Находим отношение абсолютных частот к объему выборки (3 ряд).
n = 12.
3 / 12 = 1 / 4 = 0.25
2 / 12 = 1 / 6 = 0.17
1 / 12 = 0.08
4 / 12 = 1 / 3 = 0.3
Умножим полученные значения на 100% (4 ряд).
Находим накопленные частоты путем сложения предшествующих значений. (5 ряд).
Ответ:
| варианта | 46 | 48 | 50 | 51 | 53 | 55 |
| абс. ч-та | 3 | 2 | 1 | 1 | 1 | 4 |
| относ. ч-та | 0.25 | 0.17 | 0.08 | 0.08 | 0.08 | 0.33 |
| относ. ч-та % | 25% | 17% | 8% | 8% | 8% | 33% |
| накоп. ч-та | 3 | 5 | 6 | 7 | 8 | 12 |
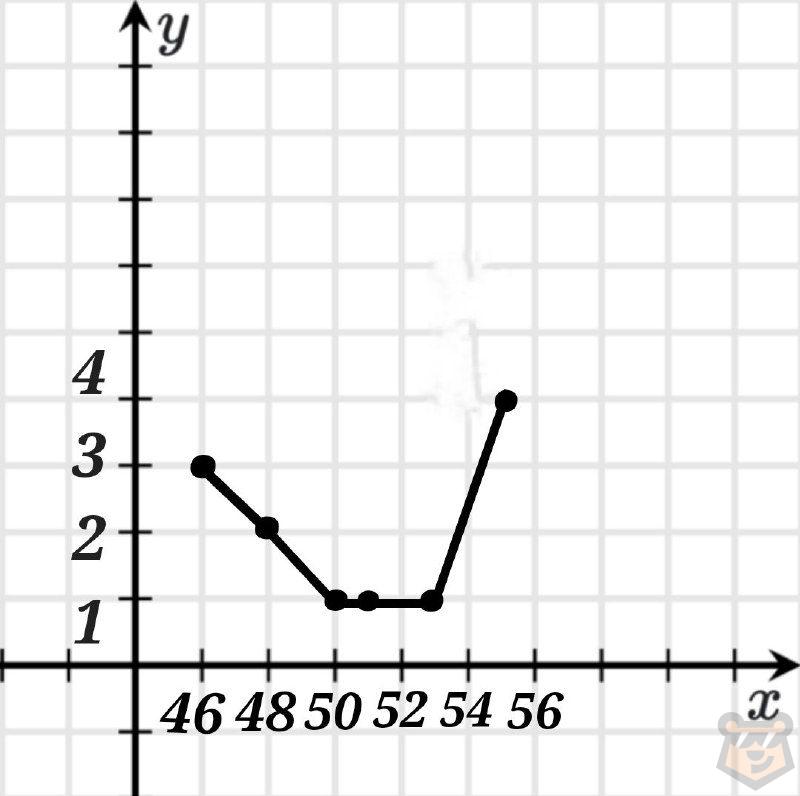
Задание №2. Дан числовой ряд: 13, 22, 14, 20, 22, 15, 17, 22, 13, 14. Определите моду, размах, медиану и среднее арифметическое данной выборки.
Решение. Упорядочим наш ряд. 13, 13, 14, 14, 15, 17, 20, 22, 22, 22.
1) Мода.
Больше всего в данной выборке встречается число 22. Поэтому оно и будет являться модой.
2) Размах.
хmax= 22
xmin= 13
22 — 13 = 9.
3) Медиана.
13, 13, 14, 14, 15, 17, 20, 22, 22, 22.
Используя либо формулу, либо логику находим в этом ряду середину.
Количество элементов четное, значит в центре у нас расположены 2 числа. Это 15 и 17. Найдем их среднее арифметическое.
(15+17) / 2 = 32 / 2 = 16.
4) Среднее арифметическое.
n=10.
(13+13+14+14+15+17+20+22+22+22) / 10 = 172 / 10 = 17.2.
Ответ: 22, 9, 16, 17.2.
Задание №3. Используя предоставленную таблицу, вычислите математическое ожидание, дисперсию и отклонение.
| xi | 5 | 7 | 8 | 10 |
| pi | 1/4 | 1/4 | 1/4 | 1/4 |
Решение. Обратимся к формулам и сделаем вычисления.
1) М(Х) = (10×1/4)+(8×1/4)+(7×1/4)+(5×1/4) = 2,5 + 2 + 1,75 + 1,25 = 7,5
2) n = 6; Х = (5 + 7 + 8 + 10) / 4 = 7.5
D = ( (5-7,5)^2 + (7-7,5)^2 + (8-7,5)^2 + (10-7,5)^2 ) / 4 = ( (-2.5)^2 + (-0,5)^2 + (0,5)^2 + (2,5)^2 ) / 4 = ( 6,25 + 0,25 + 0,25 + 6,25 ) / 4 = 13 / 4 = 3,25
3) √D = √3,25 = 1,8
Ответ: 7,5 ; 3,25 ; 1,8.
Задание №4. В цветочном магазине самый дорогой букет стоит 35 000, а самый дешевый 5000.
А) Составьте интервальный вариационный ряд с таблицей, если известно, что длина интервала равна 5000.
Решение. xmax=35000, xmin=5000, i=5000. Используем формулу.
k = (35000 — 5000) / 5000 = 30000/5000 = 6.
| х | [5000-10000) | [10000-15000) | [15000-20000) | [20000-25000) | [25000-30000) | [30000-35000) |
В) Продавец продал 27 букетов в преддверии праздника. Под конец рабочего дня он решил узнать букеты из какой подгруппы покупают чаще. И получил следующие результаты:
| хi | [5000-10000) | [10000-15000) | [15000-20000) | [20000-25000) | [25000-30000) | [30000-35000) |
| ni | 13 | 4 | ? | 3 | 1 | 2 |
Найдите сколько букетов было продано стоимостью от 10000 до 15000.
Решение. Вспомним, что сумма абсолютных частот равна объему выборки.
Вариант у нас 6, а объем равен 27.
Запишем уравнение: 13 + 4 + n + 3 + 1 + 2 = 27
23 + n = 27
n = 27 — 23
n = 4
Ответ: 4.
Задания по данному разделу, которые встречаются на ЕНТ.
Задания по данной теме на национальном тестировании присутствуют и в математической грамотности (мода, размах, среднее арифметическое и медиана), и в профильной математике (математическое ожидание, дисперсия, среднее квадратичное отклонение).
Задания сами по себе не сложные, но чтобы уж точно не потерять баллы, давайте разберем те, что чаще всего встречаются.
Математическая грамотность.
Задание № 1. Средний возраст десяти человек составляет 23 года. После того как один из людей покинул группу, средний возраст стал равным 22. Определите сколько лет было ушедшему.
Решение. В данном задании будем работать со статистической характеристикой — средним арифметическим.
Распишем начальное значение через формулу (х1+..+х10)/10=23.
Отсюда выражаем сумму всех возрастов. х1+..+х10=23×10=230
Распишем конечное значение. 1 человек ушел значит, объем выборки равен 9.
(х1+..+х9)/9=22
х1+…+х9=22×9=198
Теперь найдем возраст человека, покинувшего группу.
Мы нашли сумму 10 человек, включая ушедшего и суммы 9 человек без него.
Получается, что его возраст найдем по формуле х10=(х1+…+х10)-(х1…+х9)
х10 = 230-198 = 32.
Ответ: 32.
Задание №2. Дана таблица с вариантами и их абсолютными частотами. Используя данные определите медиану выборки.
| хi | а1 | а2 | а3 | а4 |
| ni | 2 | 9 | 2 | 6 |
Решение. Определим объем выборки. n = 2 + 9 + 2 + 6 = 19.
Число 19 нечетное, значит используем формулу: i=(n+1)/2
i = (19+1) / 2 = 20 / 2 = 10.
Для того, чтобы не расписывать весь ряд, мысленно представим его до 10 элемента.
Первые два члена это а1. От 3 до 11 находится а2. А это значит, что х10=а1.
Ответ: а2.
Задание №3. Вместо х поставьте в ряд 7, 5, 12, х, 18, 19 такие числа, чтобы размах был равен 15.
Решение. Размах = хmax — xmin
Случай 1. Представим, что х является хmin.
В таком случае получаем:
хmax — х =15
Самое большое значение в ряду равно 19. Подставляем.
19 — х = 15
х = 19 — 15 = 4
Случай 2. Пусть х является хmax.
В таком случае получаем, что
х — хmin =15
Самое маленькое значение в ряду равно 5. Подставляем.
х — 5 = 15
х = 15 +5 = 20
Ответ: 4, 20.
Задание №4. Найдите среднюю массу арбуза, опираясь на значения, представленные в таблице.
| 3 | 2 | 2,5 | 3,5 | 1,5 | 4 | 5,5 | 2 | 4 | 2 |
Решение. Воспользуемся формулой и вычислим среднее арифметическое.
(3 + 2 + 2,5 + 3,5 + 1,5 + 4 + 5,5 + 2 + 4 + 2) / 10= 30 / 10 = 3
Ответ: 3.
Математика.
Задание №1. Определите чему равна неизвестная величина, если математическое ожидание равняется 3,5.
| хi | 6 | 4 | Х | 1 |
| pi | 0,2 | 0,3 | 0,3 | 0,2 |
Решение. Распишем математическое ожидание с помощью формулы:
6×0,2 + 4×0,3 + Х×0,3 + 1×0,2 = 3,5
1,2 + 1,2 + 0,3Х + 0,2 =3,5
0,3Х = 3,5 -1,2 -1,2 — 0,2
0,3Х = 0,9
Х = 0,9 / 0,3
Х = 3
Ответ: 3.
Задания для самопроверки:
Задание 1
В представленной ниже таблице отражены набранные баллы на ЕНТ. Опираясь на эти баллы составьте таблицу абсолютных и относительных частот данного множества.
| 78 | 100 | 89 | 126 | 92 | 126 | 78 |
| 89 | 92 | 130 | 78 | 56 | 103 | 89 |
Задание 2
Представлен следующий числовой ряд: 6, 9, 10, 12, 16, 17, 23, 10, 4, 13.
Вычислите все 4 статических характеристики.
Задание 3
Опираясь на данную таблицу вычислите среднее квадратичное отклонение ряда.
| 5 | 8 | 11 | 12 | 14 |
Ответы:
1 –
| 78 | 100 | 89 | 126 | 92 | 126 | 78 |
| 89 | 92 | 130 | 78 | 56 | 103 | 89 |
2 – мода — 10, размах- 19, медиана — 11 , среднее арифметическое — 12
3 – 3.16.
