Основы теории вероятностей
Наверное почти каждый из нас слышал словосочетание «Теория вероятностей». Ассоциациями к данному понятию обычно являются игральные кости или монета, которую подбрасывают.
Однако теория вероятностей этим не ограничивается. Ее применение можно найти в самых различных сферах жизни. В список входят и наука, и техника, и экономика. Также если вы хотите в будущем стать инвестором, который вкладывает свои деньги без риска на провал, то вам стоит хотя бы поверхностно освоить эту область. Ещё важно знать, что даже в казино используют теорию вероятностей для того, чтобы максимально увеличить свою прибыль. Небольшая историческая справка: само открытие данного раздела как раз и было сделало из-за наблюдений за азартными играми. Именно поэтому среди математиков есть подобный анекдот:
Люди, которые используют теорию вероятностей в реальной жизни:
Ну и конечно же, необходимо добавить, что без основ теории вероятности не получится решить некоторые задания на едином национальном тестировании. Поэтому предлагаю приступить к изучению данной темы.
Теория вероятности —
это такой раздел математики, где изучаются случайные явления и вероятности их возникновения.
В общем смысле, вероятность описывает степень возможности наступления определенного события.
Получается, решая задачи из этого раздела, нам чаще всего будем необходимо найти вероятность того, что произойдет то или иное событие. Иногда надо узнать возникнут ли одновременно два или больше событий.
События и их виды.
С понятием вероятности мы разобрались, теперь перейдем к событиям. Что это такое?
События в теории вероятностей — это совокупность (множество) исходов, которые могут произойти в результате определенного стечения обстоятельств (эксперимента).
События могут быть разделены на следующие виды: достоверные, невозможные, случайные, совместные, несовместные, зависимые, независимые.
Достоверное событие — “событие-факт”, которое при проведении эксперимента железобетонно произойдет. Вероятность такого события равна 1.
Невозможное событие — “событие-сказка”, которому не бывать ни при каких условиях. Его вероятность равняется 0.
Случайное событие — “событие-удача”, которое может как возникнуть, так и не проявиться.
Зависимое событие — “событие-жертва абьюзивных отношений”, на которое оказывает сильное влияние другое событие.
Независимое событие — “событие-крутыш”, которому абсолютно плевать на происходящее вокруг, на нем это ни в какой степени не сказывается.
Совместные события — “события-компаньоны” могут происходить в один и тот же момент не мешая друг другу.
Вероятность случайных, зависимых, независимых и совместных событий больше 0, но меньше 1.
Несовместные события — “события-антиподы”, возникновение одного из них исключает появление другого. Сумма таких событий равна 1.
Равновероятные события — “события одного ранга”, чьи вероятности возникновения равны.
Хорошо усвоим данные определения с помощью нашего маленького помощника, котенка Чупика.

Достоверное событие | Чупик обожает молоко.  | Это всем известный факт, что коты любят молоко. |
Невозможное событие | Чупик умеет летать. | К сожалению, коты не бабочки с красивыми крыльями. |
Случайное событие | Чупик сможет поймать мышку. | Наш дружок может как поймать мышь, так и упустить ее. |
Зависимое событие | Прогулка Чупика. | В данном случае Чупик зависит от своей хозяйки, пусть ли она его на улицу. |
Независимое событие | Чупик лазает по деревьям. | Коты в таком занятии по-настоящему «свободные птицы», остановить их или снять с дерева реально трудно. |
Совместные события | Чупик лежит и думает. | Кот может одновременно и лежать, и о чем-то размышлять. |
Несовместные события | Сон Чупика и его любимый корм. | Кот не может одновременно спать и кушать, он в силах сделать сначала что-то одно, а только потом уже другое. |
Равновероятные события | Чупик и огурцы. | Отношение Чупика, как и других котов, к такому овощу в основном зависит от ситуации. Но в целом огурец в глазах кота может быть а)причиной испуга, в)лакомством, с)ничем (т.е. он пройдет мимо). Таким образом, каждый раз когда на пути Чупика встречается огурец, у нас есть 3 равновероятных исхода событий. |
Формула вероятности.
В письменных работах саму вероятность принято обозначать буквой P. А события мы записываем как любые заглавные буквы английского алфавита. Чаще всего приходиться сталкиваться с событием А и событием В.
Вероятность того или иного события обозначаем как Р(С) или Р(D).
Главная формула данного раздела выглядит так:
P(A) = m / n.
В данном выражении
P(A) — вероятность нашего события,
m — количество всех возможных результатов эксперимента,
n — количество результатов эксперимента, которые приведут к возникновению нашего события.
Рассмотрим как решается несколько примеров по данной теме и поймем как правильно пользоваться формулой.
Пример №1. В коробке находятся мячики разных цветов. Есть 7 красных, 3 зеленых и 5 фиолетовых. Найдите вероятность того, что выбранный наугад мяч будет фиолетового цвета.
Решение. Посчитаем сколько у нас всего предметов. 7 + 3 + 5 = 15. Выходит, что наугад мы может вытащить любой из этих 15 мячей. А это значит, что всего исходов у нас 15. n = 15.
Фиолетовых мячей в коробке всего 5. Значит результатов подходящих нашему событию тоже 5. m = 5.
Используем формулу и делаем вычисления.
P(A)= 5 / 15 = 1 / 3.
Ответ: 1/3.
Пример №2. В ящик сложили различные фигурки. Там было 9 красных пирамид, 5 черных пирамид и 4 черных кубика. Найдите вероятность того, что вытянутая с закрытыми глазами фигура будет а) пирамидой, b) черных.
Решение. Событие А.
Находим число всех возможных итогов. 9 + 5 + 4 = 18. n = 18
Вычислим общее количество пирамид. 9 + 5 = 14. m = 14
Делаем вычисления согласно нашей формуле
Р(А) = 14 / 18 = 7 / 9.
Ответ: 7 / 9.
Событие В.
n = 18.
Найдем количество фигур черного цвета. 4+5=9. m=9.
Используем формулу.
Р(В) = 9 / 18 = 1 / 2.
Ответ: 1 / 2.
Действия с формулами
В некоторых случаях нам необходимо перемножать, складывать вероятности, а иногда делать и то, и другое. Будет ли наше действие суммой или умножением зависит от самой ситуации.
Вероятность появления одного из двух и более несовместных событий.
В случае, где должно произойти одно из двух несовместных событий: либо событие А, либо событие В, то нам нужно к одной вероятности прибавить другую.
Р(АВ) = Р(А) + Р(В)
Пример. Найдите вероятность того, что бросая игральную кость выпадет либо 2, либо 3.
Решение. Мы можем подбросить кубик только один раз. Значит у нас выпадет не два, не три, а лишь одно число. Это будет либо 6, либо 1, либо все остальные. Таким образом, мы понимаем, что это несовместные события. Значит, будем использовать формулу: Р(АВ) = Р(А) + Р(В).
Всего у нас 6 вариантов, тогда n = 6. Цифра 2 может выпасть только 1 раз. m = 1. Выходит, что Р(А) = 1 / 6.
И тогда такая же история будет с событием В. Р(В) = 1 / 6.
Р(АВ) = 1 / 6 + 1 / 6 = 2 / 6.
Ответ: 2 / 6.
Вероятность появления двух и более независимых событий.
В случае когда нам надо найти вероятность того, что два независимых события: событие А и событие В оба произойдут, мы должны умножить их вероятности друг на друга.
P(AB) = P(А) × P(В)
Пример. Найдите вероятность того, что подкинув два раза монету, оба раза выпадет орел.
Решение. Сторона выпавшая первой, не повлияет на вторую сторону. Значит, это независимые события. Поэтому мы просто перемножим две вероятности.
У нас только два варианта, выпадает либо решка, либо орел. Получим n = 2 и m = 1. P(А) = 1 / 2.
Аналогичная ситуация со вторым событием. P(В) = 1 / 2.
Тогда выходит, что P(AB) = P(А) × P(В) = 1 / 2 × 1 / 2 = 1 / 4.
Ответ: 1 / 4.
Вероятность появления одного из двух и более совместных событий.
Когда может произойти одно из двух совместных событий, мы используем следующую формулу:
Р(АВ) = Р(А) + Р(В) — Р(АВ)
Пример. Из карточек с номерами от 1 до 20 наугад вытащили одну. Найдите вероятность того, что выбранное число будет являться четным или будет делиться на 10 без остатка.
Решение. Найдем первую вероятность. В интервале [1; 20] всего 20 чисел. n=20. Выпишем все четные числа из нашего промежутка. 2, 4, 6, 8, 10, 12, 14, 16, 18, 20. Всего выходит их 10. m=10.
Р(А) = 10 / 20 = 1 / 2.
Вычисляем вторую вероятность. Найдем в нашем интервале те числа, которые делятся на 10 без остатка. Это 10 и 20. Значит, m = 2.
Р(В) = 2 / 20 = 1 / 10.
Подставляем наши значения в формулу.
P(AB) = 10 / 20 + 2 / 20 — (1 / 2 × 1 / 10) = 12 /20 — 1 / 20 = 11 / 20.
Ответ: 11 / 20.
Вероятность появления двух и более зависимых событий.
Когда нам необходимо найти вероятность появления двух зависимых событий мы пользуемся данным выражением.
Р(АВ)=Р(А) × Р(В l А)
B l A — вероятность события В, которое зависит от того произошли ли ранее событие А.
Пример. Из колоды вытянули 2 карты. Найдите вероятность, что первой картой будет десятка, а второй картой будет дама.
Решение. Первоначально у нас в колоде 36 карт. Тогда n = 36.
Событие А. Всего семерок 4 штуки. Значит m = 4.
Р(А) = 4 / 36 = 1 / 9
Событие В. У нас осталось 35 карт в колоде, из них 4 дамы. В таком случае n = 35, m = 4.
Р(B l A) = 4 / 35.
Вычисляем Р(AB).
P(AB) = 1 / 9 × 4 / 35 = 4 / 315.
Ответ: 4 / 315.
| Количество и вид событий. | Слова-помощники. | Формула. |
| Произойдет 1 из 2 несовместных событий. | Либо, или | Р(АВ) = Р(А) + Р(В) |
| Произойдут 2 независимых события. | И, вместе | P(AB) = P(А) × P(В) |
| Произойдет 1 из 2 совместных событий. | Либо, или | Р(АВ) = Р(А) + Р(В) — Р(АВ) |
| Произойдут 2 зависимых события. | Первый, второй, если | Р(АВ)=Р(А) × Р(В l А) |
Практическая часть.
Задание №1. Студент выучил 12 билетов. Какова вероятность того, что он из 20 билетов вытянет тот, к которому не готов ?
Решение. Найдем количество билетов, который студент не учил. 20-12=8. m=8.
Всего у него 20 билетов.
Р(А) = 8 / 20 = 2 / 5.
Ответ: 2 / 5.
Задание №2. В мешке 4 синих и 6 красных кубиков. Найдите вероятность того, что первый вытянутый куб будет красным, а второй — синим.
Решение.
Событие А. n = 10, m = 6.
Р(А) = 6 / 10 = 3 / 5.
Событие В. Один куб уже забрали. Значит n = 9, m = 6.
Р(В) = 4 / 9.
Поскольку это зависимые события будем использовать формулу Р(АВ)=Р(А) × Р(В l А)
Р(АВ) = 3 / 5 × 4 / 9 = 12 / 45 = 4 / 15.
Ответ: 4 / 15.
Задание №3. Найдите вероятность того, что набранный балл по математической грамотности на ЕНТ будет выше порогового и будет четным числом.
Решение. Максимальный балл — 10. n = 10.
Событие А. Пороговый балл 3. Выше его 4, 5, 6, 7, 8, 9, 10. m = 7.
Р(А) = 7 / 10 = 0,7
Событие В. Из интервала {4, 5, 6, 7, 8, 9, 10} выберем четные числа. 4, 6, 8, 10. m = 4.
Р(В) = 4 / 10 = 0, 4.
Случай, когда набранный балл будет выше 3 и будет четным, является появлением двух независимых событий. Тогда нужна формула P(AB) = P(А) × P(В).
P(AB) = 0,4 × 0,7 = 0,28
Ответ: 0,28.
Задания по данному разделу, которые встречаются на ЕНТ.
Задачи на основы теории вероятностей попадаются и в математической грамотности, и в профильной математике. Поэтому давайте решим несколько задач, которые могут вам встретиться на тестировании.
Математическая грамотность.
Задание №1. В пенале лежат 7 фломастеров, 5 ручек и 24 карандаша. Вычислите вероятность того, что выбранный наугад предмет будет являться карандашом.
Решение. Найдем общее количество школьных принадлежностей. 7 + 5 + 24 = 36. n = 36.
Карандашей у нас 24, значит m = 24.
Используем нашу основную формулу Р = m / n.
P = 24 / 36 = 2 / 3
Ответ: 2 / 3.
Задание№2. На фабрике для выполнения работы используют двух роботов. Машины работают независимо друг от друга. Вероятность того, что первый робот не выйдет из строя равна 0,96, а вероятность второго 0,85. Каков шанс того, что один из роботов сегодня окажется неисправным ?
Решение. Есть только две ситуации, когда работать будет только один из роботов.
А) Когда первый робот исправен, а второй вышел из строя.
В) Когда второй робот исправен, а первый вышел из строя.
Событие А.
- Сперва вычислим вероятность того, что у второй машины будет сбой в работе.
Обратим внимание на то, что в данном случае сбой и исправность исключают друга друга, а это значит, что они являются несовместными событиями. Тогда сумма их вероятностей будет равно 1. Используя это свойство найдем нужную вероятность.
Р(В) + Р(В’)= 1 Р(В’) = 1 — Р(В) = 1 — 0,85 = 0,15
- А вот теперь можем найти шанс того, что в то время как будет работать первый робот, второй будут чинить.
Согласно условиям это будет появлением двух независимых событий. Значит будем использовать формулу P(AB) = P(А) × P(В).
Р(АВ’) = P(А) × P(В’) = 0,96 × 0,15 = 0,144
Событие В.
- Опять нужно для начала найти вероятность того, что первому роботу потребуется ремонт. Тут такая же ситуация как и со вторым роботом.
Р(А) + Р(А’) = 1 Р(А’) = 1 — 0,96 = 0,04
- Сейчас вычисляем вероятность события А’В, которое тоже будет являться умножением двух независимых событий А’ и В.
Р(А’В)= P(А’) × P(В) = 0,04 × 0,85 = 0,034
События АВ’ и А’В.
Теперь найдем вероятность того, что произойдет одна из данных ситуаций. Внимательно прочитаем наше решение и поймем, что эти два события являются несовместными. Потому что ни один из роботов не может одновременно быть и сломанным, и исправным. А значит мы будем находить вероятность одного из двух несовместных событий согласно формуле: Р(АВ) = Р(А) + Р(В).
Р = Р(АВ’) + Р(А’В) = 0,144 + 0,034 = 0,178.
Ответ: 0,178.
Математика.
Задание №1. В круг, радиус которого равен 6 см, вписан квадрат. Вычислите вероятность того, что брошенный наугад дротик не попадет в квадрат.
Решение.
- Вероятность попадания в круг, а не в квадрат будет находиться по формуле Р=S2/S.
- S2 — это площадь той части круга, которую не перекрывает наш квадрат. Найдем значение S2, отняв от площади круга площадь квадрата. Получим S2 = S — S1.
- S — это площадь всего круга, т.е. все возможны исходы. Вычислим это по формуле S=πr^2.
- S1 — это площадь квадрата. Мы знаем, что ее вычисляют по формуле S=а^2.
- Нам надо найти чему равна сторона квадрата. Для этого вспомним формулу, связывающую сторону квадрата и диаметр описанной около него окружности: а=d/√2.
- Используя свойства круга и окружности представим d через r.
Мы расписали наш план действий. Теперь будем преобразовывать наши формулы соблюдая составленный алгоритм снизу вверх. А сами вычисления сделаем после того, как справимся с формулами.
- d=2r.
- Подставляем d=2r в формулу а=d / √2. Получим: а=2r / √2
- Подставляем а = 2r / √2 в выражение S = а^2. Выйдет S1 = (2r / √2)^2 = 4r^2 / 2 = 2r^2.
- S=πr^2.
- S2 = S — S1 = πr^2 — 2r^2 = r^2 × (π — 2)
- Р=S2/S = r^2 × (π — 2) / πr^2
Смотря на нашу конечную формулу понимаем, что можем сократить r^2 и в числителе, и в знаменателе. И тогда получим: Р = (π — 2) / π. Это и будет нашей вероятностью.
Ответ: (π — 2) / π.
5 заданий по контексту.
Мишень.
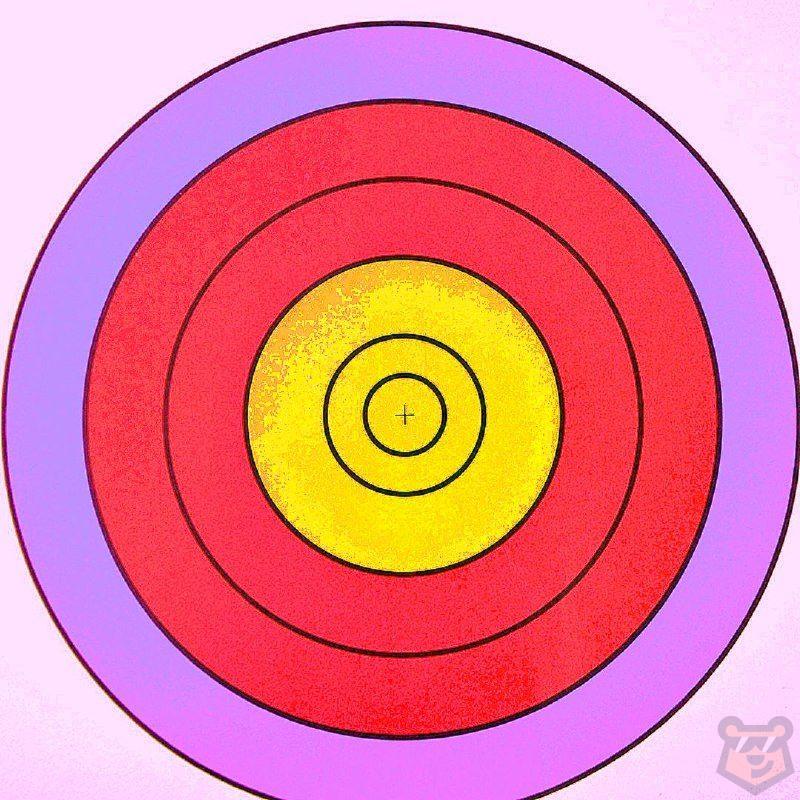
Мишень разделена на три части: желтую, розовую и фиолетовую. Два стрелка стреляют по мишени и всегда поражают один из секторов. Вероятность попадания первого стрелка в фиолетовую часть мишени равна 0,35, а в розовую — 0,25. Вероятность попадания в желтую часть второго стрелка равна 0,6.
Вопрос №1. Найдите вероятность того, что первый стрелок попал в желтую часть мишени
Решение. В задании сказано, что стрелки ВСЕГДА попадают по мишени. Значит у каждого стрелка каждый выстрел имеет только три исхода А, В и С, которые означают попадание в фиолетовую, розовую и желтую части соответственно.
Мы понимаем, что А, В и С это несовместимые события, ведь наши стрелки могут попасть только в одну из частей мишени. А это значит, что сумма их вероятностей равна 1. И отталкиваясь от этого, вычислим вероятность попадания в желтую часть мишени первым стрелком.
Р(А1) + Р(В1) + Р(С1) = 1
Р(С1) = 1 — Р(А1) — Р(В1) = 1 — 0,35 — 0,25 = 0,4
Ответ: 0,4.
Вопрос №2. Найдите вероятность того, что первый стрелок попал в розовую или фиолетовую часть мишени.
Решение. Как мы говорили ранее это будут несовместные события. А вероятность появления одного из нескольких несовместных событий находят по формуле Р(АВ) = Р(А) + Р(В).
Р(А1В1) = 0,35 + 0,25 = 0,6
Ответ: 0,6.
Вопрос №3. Найдите вероятность того, что первый стрелок попал в желтую часть мишени, а второй стрелок не смог этого сделать.
Решение. Стрелки никаким образом друг на друга не влияют. Выходит, это два независимых события, вероятность которых принято вычислять с помощью выражения P(AB) = P(А) × P(В).
1) Вспоминаем, что Р(С1) = 0,4.
2) Находим Р(А2В2). Ранее мы уже говорили, что А, В и С это несовместимые события. Значит, Р(С2) + Р(А2В2) = 1.
Р(А2В2) = 1 — Р(С2) = 1 — 0,6 = 0,4
3) Р = Р1 × Р2 = 0,4 × 0,4 = 0,16
Ответ: 0,16.
Вопрос №4. Чему равен шанс того, что желтая часть мишени будет поражена только одним из стрелков, если всего каждый сделал по одному выстрелу ?
Решение. В данном случае у нас будет два варианта развития событий:
А) Попал первый стрелок, но не попал второй.
В) Попал второй стрелок, но промахнулся первый.
Каждое из них будет являться ничем иным, как появлением одного из двух независимых событий. Тогда мы должны использовать формулу P(AB) = P(А) × P(В).
Событие А.
Р(С1) = 0,4.
Р(А2В2) = 1-0,6 = 0,4
Р(А) = 0,4 × 0,4 = 0,16
Событие В.
Р(С2) = 0,6
Р(А1В1)= 1 — 0,4 = 0,6
Р(В) = 0,6 × 06 = 0,36 Р(С1С2)= Р(С1) + Р(С2) —
Событие АВ.
Событие А и событие В это несовместимые события, потому что у нас должно быть только одно попадание. А значит мы используем формулу Р(АВ) = Р(А) + Р(В).
Р(АВ) = 0,36 + 0,16 = 0,52
Ответ: 0,52.
Вопрос №5. Первый стрелок произвел пять выстрелов. Какова вероятность того, что он ровно 3 раза поразил желтую часть мишени.
Решение. Данные пять выстрелов будут являться независимыми событиями. Вероятность появления, которых принято вычислять по формуле P(AB) = P(А) × P(В).
Допустим первые три выстрела он попал. Тогда мы получим, что Р1 = Р2 = Р3 = 0,4.
Выходит, что последние два раза он попал либо в розовую, либо в фиолетовую части. В таком случае Р4 = Р5 = 0,6.
Используя формулу, у нас выйдет следующее выражение. Р = Р1 × Р2 × Р3 × Р4 × Р5 = 0,4 × 0,4 × 0,4 × 0,6 × 0,6 = 0,02304
Ответ: 0,02304.
Задания для самопроверки:
Задание 1
Найдите вероятность того, что подбросив две игральные кости у нас выпадет два числа, сумма которых будет равна 7.
Задание 2
Какова вероятность того, что вытянутая наугад карта из колоды окажется либо тузом, либо шестеркой ?
Задание 3
Вероятность купить бракованный утюг в одном магазине равна 0,3 , а во втором 0,2. Вычислите вероятность того, что ходя бы один из двух купленных утюгов окажется бракованным.
Ответы:
1 – 1/6.
2 – 2/9.
3 – 0,44.

 4,00/5
4,00/5