Основы комбинаторики
Область математики, которая называется «Комбинаторика», является эффективным средством как и для теоретических исследования, так и для решения практических заданий из абсолютно разных отраслей. Например, это могут быть современные информационные технологии, физика, экономика и даже биология.
С комбинаторикой тесно связаны все наши пароли от социальных сетей и передача засекреченной информацией в вооруженных силах с помощью шифрования. В общем данный раздел охватывает широкий спектр услуг, начиная криптографией и заканчивая теорией игр.
Но несмотря на то, что комбинаторика имеет прямое отношение к повседневной жизни, многие школьники все равно не особо любят решать задачи по ней. И это ещё мягко сказано. Ведь реакция большинства учащихся на этот раздел выглядит примерно так:

Однако не стоит отчаиваться раньше времени. Предлагаем вам вместе с нами разобраться с данной темой для того, чтобы убедиться, что комбинаторика не самая страшная область математики и, конечно, для того, чтобы не потерять драгоценные баллы на ЕНТ, где встречаются задания по этому разделу.
Комбинаторика, что это ?
Естественно, все мы понимаем, что сам термин произошел от слова комбинация. Значит, можно сделать вывод, что комбинаторика исследует различные комбинации ? Абсолютно верно.
Комбинаторика – это фрагмент математики, основой которого является изучение разнообразных перестановок элементов из множеств и подсчет количества всевозможных комбинаций из этих элементов.
Ключевые понятия в комбинаторике.
Так называемый фундамент данного раздела математики составляют 3 вещи: сочетания, размещения и перестановки. Давайте поближе познакомимся с каждым из данных понятий.
Перестановки.
В широком смысле люди понимают это как перераспределение каких-либо предметов, перенос их с одного места на другое. В комбинаторике примерно такое же значение.
Представим, что у нас есть определенное количество элементов. Обозначим данное множество буквой n.
Допустим, наши элементы решили образовать очередь. Сделать они это могут абсолютно по-разному. Потому что если даже два элемента поменять местами, мы получим уже абсолютной другой ряд.
Также стоит обращать внимание на то, что наша очередь всегда будет состоять из всех элементов множества n, не внося никакие изменения в состав. То есть у нас было 3 женщины в списке, значит в каждой очереди обязательно будут эти 3 женщины и такое с каждым компонентом нашей совокупности.
Таким образом получается, что перестановки — это число многообразных изменений в расположении элементов с учетом того, что количество самих элементов остается неизменным.
Давайте, на примере героев мультфильма «Губка Боб Квадратные Штаны» составим разные перестановки.
У нас есть 3 элемента (3 героя): Губка Боб, Патрик и Сквидвард. Сейчас мы будем всеми возможными способами переставлять их.
1 |  |  | |
2 |  |  | |
3 |  |  | |
4 |  |  | |
5 |  |  | |
6 |  |  |
В итоге благодаря этой таблице мы смогли посчитать количество перестановок, когда у нас всего 3 элемента, и так у нас вышло аж 6 способов изменить расположение компонентов. Но как нам быть с теми множествами, где у нас 25 или 43 элемента ? Как посчитать перестановки не расписывая ряды и не составляя таблицу ?
А для этого, существует формула:
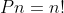
n! — это факториал числа n.
Факториал числа n является результатом перемножения всех чисел в ряду от 1 до нашего числа n.
Например, 2! = 1 × 2 = 2,
3! = 1 × 2 × 3 = 6,
4! =1 × 2 × 3 × 4 = 24 и так далее.
Размещения.
Для того чтобы лучше понять, что это такое, сразу же приступим к примеру.
Допустим, у нас есть множество элементов n. Из данной совокупности мы должны выбрать m элементов, а после сгруппировать их как только можем. Обращать внимание на порядок m элементов нужно.
Давайте представим, что нам необходимо из нашего множества n назначить лидера, его заместителя и их помощника. Значит, у нас будут получаться группы по типу А+В+С, D+E+F. Но комбинации из элементов, например, А, В и С будут повторяться по несколько раз, потому что для нас важен порядок. Ведь в группе А+В+С, А — это лидер, В — его заместитель, С — их помощник. А вот в группе С+В+А, наоборот, С — лидер, В — заместитель, А — помощник и так далее.
Таким образом, размещения — это количество группировок из m элементов, отобранных из множества n, с учетом того, что из одних и тех же элементов могут создаваться несколько комбинаций.
Предлагаем на примере персонажей из серии всем известных анимационных фильмов «Кунг-фу Панда» до конца разобраться в размещениях.
У нас опять 3 элемента. Это По, Мастер Тигрица и Мастер Шифу.
Представим, что из данной троицы нам необходимо составить всевозможные пары для проведения тренировок. Один из пары будет показывать приемы, а второй будет тем, на ком первый эти приемы отрабатывает.
| № | Демонстратор | “Груша для битья” |
1 |  |  |
2 |  |  |
3 |  |  |
4 |  |  |
5 |  |  |
6 |  |  |
Выходит, у нас может быть только 6 пар.
С целью упростить вычисления и сэкономить потраченное на них время, математики вывели формулу для нахождения числа размещений.
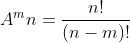
Давайте попробуем сделать вычисления по нашему примеру с помощью формулы. Нам надо найти размещения по 2 элемента (m) из 3 (n). Мы просто подставляем наши числа в формулу и решаем.
В итоге получим:
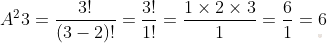
Сочетания.
В стандартном понимании, сочетание — это соединение нескольких элементов. В комбинаторике у данного термина похожий смысл. Убедимся в этом на нескольких примерах.
Давайте предположим что у нас есть совокупность элементов. Назовем ее n. Из нее нам необходимо взять определенное количество m элементов и сгруппировать их. Сделать это надо с учётом того, что порядок в данных группировках ключевой роли не играет. То есть, из одинаковых элементов мы в силах сделать только одну группу, одно сочетание.
Таким образом, сочетания — это количество групп, которые составлены из элементов m, взятых из совокупности n, и в них порядок не важен.
Давайте с помощью мультфильма «Фиксики» лучше это усвоим.
Представим, что нам надо из 3 наших героев (Симка, Нолик и Фаер) выбрать 2 дежурных. Составим таблицу и посчитаем сколько пар можно составить.
1 |  |  |
2 |  |  |
3 |  |  |
Для нас порядок не важен. Например, если мы запишем «Сегодня дежурные: Симка и Нолик» или «Сегодня дежурные: Нолик и Симка» смысл у нас не поменяется. Дежурят они оба, а кто стоит первым или вторым в списке никакой роли не играет.
Для того чтобы вновь не мучиться с вычислениями была выведена формула.
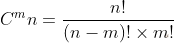
Предлагаю по нашему случаю сделать решение с помощью данного выражения. Получим следующее:
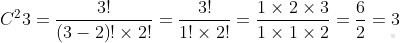
Заключительная таблица с формулами.
| Перестановки. | |
Размещения. | |
Сочетания. |
Решение задач.
Для решения того или иного задания по комбинаторике прежде всего необходимо определить с чем мы имеем дело. Перед нами перестановки, размещения или сочетаниями? Обычно именно это и является самым трудным для учеников.


Чтобы процесс со стороны не выглядел как на представленных иллюстрациях, предлагаю вам ознакомиться со следующей таблицей, которая поможет правильно выбрать формулы.
Задействованы все элементы, порядок имеет значение | Задействована только часть элементов, порядок имеет значение, из одних и тех же элементов можно составить несколько групп. | Задействована только часть элементов, порядок не имеет значение, из одних и тех же элементов можно составить только 1 группу. |
| Перестановки. | Размещения. | Сочетания. |
Определившись с формулой мы просто делаем вычисления и таким образом находим ответы.
Практическая часть.
Задание №1. Сколькими способами можно построить башню из 8 кубиков, если их нужно ставить один на другой.
Решение. Для построения башни мы конечно же собираемся использовать все кубики и их порядок для нас важен. Значит это перестановки. Сделаем вычисления, используя формулу:

Р8=8!=1×2×3×4×5×6×7=5040
Ответ: 5040.
Задание №2. Из 8 человек необходимо выбрать 5 для основного состава во время игры. Сколько таких пятерок можно составить ?
Решение. Задействована только часть нашей совокупности, порядок для нас не важен, потому что каждый из 5 человек как ни крути будет являться частью команды и не важно какое место будет занимать его имя в списке. Выходит, что это сочетания. Значит, нам надо искать ответы с помощью выражения:
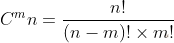
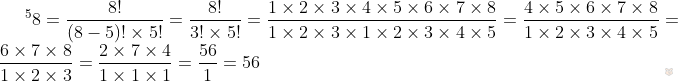
Ответ: 56.
Задание №3. Участвуя в конкурсах от организации рабочие могут выиграть один из 9 брелоков и один из 6 термосов. Сколько всего есть комбинаций для победивших ?
Решение. Выиграть 1 из 9 брелоков можно 9 способами. Это понятно даже без формул. Потому что нам может выпасть любой из 9 предметов. Такая же схема и с термосами. У нас есть 6 способов получить один из них. Получается:
брелоки — 9;
термосы — 6.
Тогда сколькими способами можно выбрать «брелок+термос» ?
Все очень просто необходимо полученные значения перемножить.
9 × 6 = 56
Ответ: 56.
Задания по данному разделу, которые встречаются на ЕНТ.
Знание основ комбинаторики пригодится при решении заданий как и из раздела «математическая грамотность«, так и из профильной математики. Поэтому давайте посмотрим как решаются те типы задач, с которыми можно столкнуться.
Математическая грамотность.
Задание №1. Сколько образов можно сделать из 6 рубашек, 4 брюк и 3 пар обуви?
Решение. Это задача похожа на ту, что мы решали в практической части. Алгоритм действий точно такой же.
Рубашки — 6 вариантов; брюки — 4 варианта; обувь — 3 варианта.
«Рубашка+брюки+обувь» = 6 × 4 × 3 = 72
Ответ: 72.
Задание №2. В классе из 13 учеников необходимо назначить старосту, человека, отвечающего за сектора спорта и того, кто будет следить за цветами в кабинете. Сколькими способами мы можем составить данную тройку ?
Решение. Задействована только часть элементов, порядок для нас важен, ведь одна и та же троица может занимать разные должности. Выходит, что это размещения и нам нужно использовать формулу:
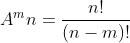
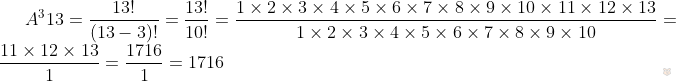
Ответ: 1716.
Математика.
Задание №1. Решите данное выражение:
Решение. Используем все три наши формулы и делаем все необходимые вычисления.
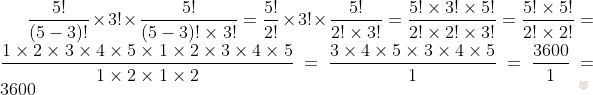
Ответ: 3600.
Задание №2. Сколько существует способов для выбора 2 мальчиков из 12 и 2 девочек из 7 для сценки на школьном концерте ?
Решение. И там, и там задействована лишь некая часть множества, порядок не имеет значение. Таким образом мы делаем вывод, что это сочетания. С помощью подходящей формулы найдем С1 и С2.
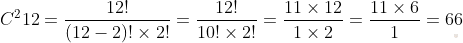
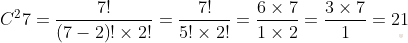
Теперь найдем «девочки+мальчик». С = С1 × С2
66× 21=1386
Ответ: 1386.
Задания для самопроверки:
Задание 1
Сколько может быть составлено расписаний на 1 день из 6 уроков ?
Задание 2
Сколькими способами можно из 11 человек выбрать троих атакующих: форварда, крайнего нападающего и полусреднего нападающего ?
Задание 3
Для старшеклассников на профориентации дали лист с 8 пунктами, из них им нужно выбрать только 4 самых важных. Сколько комбинаций можно получить ?
Ответы:
1 – 120.
2 – 990.
3 – 70.
