Логические последовательности

Если вы думали, что после геометрической прогрессии больше ничего не сможет заставить вас чувствовать отвращение к такому разделу, как «Последовательности», с новой силой, то вы глубоко заблуждались. Потому что существуют еще этакие злодеи под названием «Логические последовательности». Вот их действительно многие недолюбливают. Для того, чтобы понять почему, будет достаточно посмотреть на иллюстрацию.
Благодаря данной картинке можно прийти выводу, что логические последовательности во многом отличаются от других. Поэтому изучая их, у нас не получится проводить аналогии, как это было при работе с арифметической и геометрической прогрессиями. Но это не значит, что умение разбираться в логических последовательностях является каким-то чудом. Просто нужно быть готовым к некоторым подводным камням, ну и, конечно, же не забывать включать самое главное — логику.
Логическая последовательность-
это такой ряд элементов, в котором каждый новый член получают с помощью определенного логического правила или закона.
Как говорилось раньше, такие последовательности сильно выделяются на фоне других. А именно потому что они имеют отличия не только в самой своей сути, но и в принципах и алгоритмах решения.
Например, для арифметической и геометрической прогрессий есть свои конкретные формулы, которыми мы пользуемся во время выполнения заданий, их достаточно много и каждую необходимо знать наизусть. А вот для решения логических последовательностей нет необходимости заучивать такое большое количество формул. Ведь самих формул нет. Все ряды имеют свою особую закономерность, поэтому универсального метода решения, который бы подходил для каждого случая, не существует.
Поэтому для любой логической последовательности мы должны самостоятельно определить правило или правила (да, иногда бывает и так), по которым формируется ряд элементов. И только после этого мы можем приступить к решению самого задания, чаще всего оно заключается в нахождении следующего или пропущенного числа.

Виды логических последовательностей
В зависимости от закономерности, по которой находятся элементы, логические последовательности могут быть самыми разными. Их видов больше, чем у арифметических и геометрических прогрессий вместе взятых. Выделим самые основные.
1) Ряд простых чисел — это самая легкая для понимания разновидность логических последовательностей.
Простым числом называют то число, которое без остатка делиться только на себя и на единицу.
Выглядит данная последовательность таким образом: {2, 3, 5, 7, 11, 13, 17, 19…}
2) Последовательности, основанные на принципе сложения/вычитания. Каждый элемент таких последовательностей равен сумме или разности двух предыдущих.
Пример 1. {3, 3, 6, 9, 15, 24, 39…}
0+3=3
3+3=6
3+6=9
6+9=15
Пример 2. {10, -10, 20, -30 …}
0-10=-10
10-(-10)=20
-10-20=-30
20-(-30)=50

Самым известным числовым рядом, построенным по данному правилу, является Фибоначчиева последовательность. Это чуть ли не единственная логическая последовательность, у которой есть свое название и которая отличается особой конкретикой.
Числа Фибоначчи представляют собой следующий ряд:
{0, 1, 1, 2, 3, 5, 8, 13, 21…}
Для решения задач, которые непосредственно связаны с самой Фибоначчиевой последовательностью, будет достаточно запомнить несколько первых членов, и уже отталкиваясь от этого делать все необходимые вычисления.
3) Последовательности, построенные на принципе умножения/деления. Каждый элемент находят путем деления или умножения двух предыдущих друг на друга .
Пример 1. {1, 2, 2, 4, 8, 32, 256…}
1×2=2
2×2=4
2×4=8
4×8=32
Пример 2. {64, 16, 4, 4, 1, 4, 1/4… }
64÷16=4
16÷4=4
4÷4=1
4÷1=4
Еще последовательности такого типа могут строиться исходя из того, что одно какое-то число нужно, например, разделить на порядковый номер элемента.
Пример 3. Рассмотрим такой вариант с единицей в главной роли.
{1, 1/2, 1/3, 1/4, 1/5, 1/6…}
1÷1=1
1÷2=1/2
1÷3=1/3
1÷4=1/4
4) Степенные последовательности. Из названия понятно, что данный вид последовательностей связан со степенями.
Такие ряды могут состоять из одного числа, возведенного в разные степени.
Пример 1. Последовательность степеней числа 5: {1, 5, 25, 125, 625…}
5^0=1
5^1=5
5^2=25
5^3=125
Но также данные последовательности могут представлять из себя ряд натуральных или любых других чисел, которых возвели в одну конкретную степень, например кубическую или квадратную.
Пример 2. {1, 8, 27, 64, 125, 216…}
Перед вами натуральные числа в третьей степени.
1^3=1
2^3=8
3^3=27
4^3=64
5) Смешанные. Один такой ряд сочетает в себе две или более последовательности с разными логическими законами.
Пример 1. {1, 1, 4, 8, 9, 27…}
Этот ряд можно разделить на три отдельные пары:
1) {1, 1}
2) {4, 8}
3) {9, 27}
И теперь нам не составит труда разглядеть тут квадратные и кубические степени разных чисел.
1) 1^2=1 1^3=1
2) 2^2=4 2^3=8
3) 3^2=9 3^3=27
Пример 2. {3, 5, 9, 13, 15, 21, 21, 29…}
Разложим данную последовательность таким образом, что в первом ряду будут только черные числа, а в другом только красные. {3, 5, 9, 13, 15, 21, 21, 29…}
В итоге получим следующее:
1) {3, 9, 15, 21}
2) {5, 13, 21, 29}
Хорошо присмотревшись увидим, что в черном ряду каждый последующий член больше предыдущего на 6.
3+6=9
9+6=15
15+6=21
А во втором случае для того, чтобы получить новую составляющую, нам нужно к предшествующей прибавить 8.
5+8=13
13+8=21
21+8=29
6) Алгоритмические последовательности.
Это такие последовательности, где для того, чтобы найти чему равен новый элемент, нужно сделать целую комбинацию действий с предыдущими членами.
Может быть случай, где необходимо задействовать и степени, и деление. Бывает вариант, в котором надо и сложить, и умножить.
Проще говоря, к данной группе последовательностей относятся те ряды, метод построения которых сочетает в себе два или более действий, условий.
Пример 1. {1, 9, 144, 21904…}
Для начала мы прибавляем к предыдущему члену порядковое числительное нового элемента, а затем полученное число возводим в квадрат.
(0+1)^2=1
(1+2)^2=9
(9+3)^2=144
(144+4)^2=21904
Пример 2. {1, 1/4, 1/9, 1/16, 1/25…}
Для продолжения такого ряда нам необходимо делить единицу на порядковый номер, который предварительно был возведен во вторую степень.
1/(1^2)=1
1/(2^2)=1/4
1/(3^2)=1/9
1/(4^2)=1/16
Бывает так, что у одного ряда можно найти несколько закономерностей. Это абсолютно нормально, пугаться этого не стоит. Рассмотрим один такой случай.
Пример 3. {1, 3, 7, 15, 31…}
Есть два способа решения:
№1. Для того, чтобы найти следующий член данной последовательности, мы возводим 2 в степень, которая соответствует его порядковому числительному, а после отнимаем 1.
(2^1)-1=1
(2^2)-1=3
(2^3)-1=7
(2^4)-1=15
№2. Мы к предшествующей составляющей прибавляем степени числа 2.
0+2^0=1
1+2^1=3
3+2^2=7
7+2^3=15
Пример 4. {4, 16, 36, 64, 100, 144…}
Данная последовательность состоит из четных чисел во второй степени.
2^2=4
4^2=16
6^2=36
8^2=64
Пример 5. {1, 27, 125, 343..}
А этот ряд у нас представлен нечетными числами, возведенными в кубическую
степень.
1^3=1
3^3=27
5^3=125
7^3=343


Практическая часть.
Для закрепления теоретического материала перейдем к практике и выполним несколько задач.
Задание №1. Найдите пропущенное число в последовательности
{3, 6, 18, 72, ?, 2160, 15120}.
Решение. Можно заметить, что каждый новый член равен произведению его порядкового номера на предыдущий элемент.
3×2=6
6×3=18
18×4=72
2160×7=15120
Получается неизвестный компонент находим так:
72×5=360
Ответ: 360.
Задание №2. Найдите последний член в числовом ряду {4, 10, 33, 136, 685, ?}.
Решение. Если внимательно посмотреть на данную нам последовательность, то можно понять ее закономерность, которая заключается в том, что каждый член равен сумме единицы и предыдущего элемента, умноженной на его порядковый номер.
(4+1)×2=10
(10+1)×3=33
(33+1)×4=136
(136+1)×5=685
Выходит для того, чтобы найти нужное нам число, мы сделаем такого рода вычисления:
(685+1)×6=4116
Ответ: 4116.
Задание №3. Найдите неизвестный элемент последовательности {4, 11, 30, 85, ?}.
Решение. Рассмотрев все возможные варианты, находим наш логический закон:
Для вычисления нового члена необходимо найти сумму его порядкового номера и тройки, возведенной в степень равной индексу члена.
1+(3)^1=4
2+(3)^2=11
3+(3)^3=30
4+(3)^4=85
Отталкиваясь от нашего правила, находим последний член:
5+(3)^5=248
Ответ: 248.
Задания по данному разделу, которые встречаются на ЕНТ.
Хотя бы одну логическую последовательность на ЕНТ в основном привыкли встречать в разделе “Математическая грамотность”. Но и в профильной математике иногда попадаются 1-2 задания по данной теме. Поэтому давайте разберем задачи, с которыми можно столкнуться на Едином национальном тестировании.
Математическая грамотность:
Задание №1. Установите закономерность и определите следующий член последовательности: {2, 3, 6, 11, 18, …}
Решение. Можно увидеть, что все новые составляющее равны сумме предыдущего элемента и нечетного числа.
Для простоты понимания наглядно покажем данный алгоритм.
{1, 3, 5, 7, 9, …} — это ряд нечетных чисел, расположенный по порядку. Данным рядом мы будем пользоваться для определения последующих компонентов нашей последовательности.
2+1=3
3+3=6
6+5=11
11+7=18
Выходит нужный нам член вычисляется таким образом:
18+9=27
Ответ: 27.
Задание №2. Пятый элемент последовательности {0, 7, 26, 63, …} равен…
Решение. При внимательном изучении чисел, легко заметить, что если к ним прибавить по единице, то мы получим кубическую степень натуральных чисел.
0+1=1 1=1^3
7+1=8 8=2^3
26+1=27 27=3^3
63+1=64 64=4^3
Натуральное число, которое возводится в третью степень, равно порядковому номеру элемента. Тогда наша закономерность звучит так: Каждый член равен разности его порядкового индекса в кубической степени и единицы.
И выходит, что искомый нами член будет найден благодаря следующим вычислениям:
(5^3)-1=124
Ответ: 124.
Задание №3. Дана последовательность {2, 4, 8, 3, 9, 27, 4, х, 64}. Определив закономерность, найдите чему равен х.
Решение. Для начала разделим последовательность на три части. Получим:
1) {2, 4, 8}
2) {3, 9, 27}
3) {4, х, 64}
Теперь видно то, что каждый ряд это последовательность степеней одного определенного числа.
1) 2^1=2 2^2=4 2^3=8
2) 3^1=3 3^2=9 3^3=27
3) 4^1=4 х 4^3=64
В итоге приходим к выводу, что х=4^2. х=16
Ответ: 16.
Задание №4. Найдите недостающее число в последовательности.
453 (564) 675
342 (х) 746
137 (199) 261
Решение. Рассмотрев все возможные варианты комбинаций, легко понять, что элемент посередине равен полусумме крайних чисел.
(453+675)÷2=564
(137+261)÷2=199
В таком случае неизвестное найдем так:
(342+746)÷2=544
Ответ: 544.
Задание №5. Внимательно изучив таблицу, установите закономерность и найдите неизвестный член.
| 169 | 25 | 12 |
| 25 | 16 | 3 |
| 225 | 144 | ? |
Решение. Тщательно рассмотрев числа, нетрудно заметить, что необходимо работать с квадратами и корнями.
Закономерность таблицы заключается в том, что элемент в последнем столбце является корнем из разности двух предыдущих чисел.
√(169-25)=√(144)=12
√(25-16)=√(9)=3
И тогда наш недостающий член будет равен:
√(255-144)=√81=9
Ответ: 9
Профильная математика:
Задание №6. Используя таблицу, определи чему равен 7 член последовательности.
| порядковый номер | 1 | 2 | 3 | 4 | 5 | 6 |
| член | 2 | 3/4 | 4/9 | 5/16 | 6/25 | 7/36 |
Решение. Опираясь на данные таблицы, мы понимаем, что для поиска нужного элемента мы должны прибавить к его порядковому номеру единицу, а полученное значение разделить на квадрат его индекса. То есть алгоритм решения выглядит так:
1+1/(1^2)=2/1=2
2+1/(2^2)=3/4
3+1/(3^2)=4/9
Используя это правило, найдем 7 член:
7+1\(7^2)=8/49
Ответ: 8/49.
Задание №7. Из предложенных ниже вариантов, найдите общую формулу для n-члена последовательности: {1/(2×3), 2/(3×5), 3/(5×7), 4/(7×9)}.
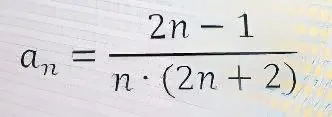 А)
А)
 В)
В)
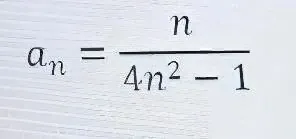 С)
С)
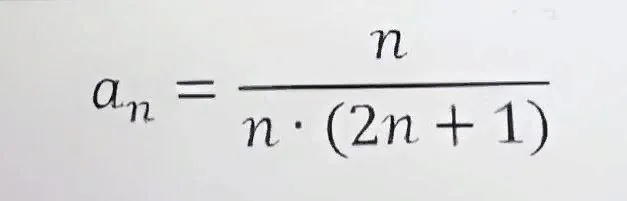 D)
D)
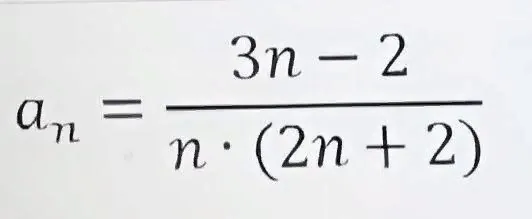 E)
E)
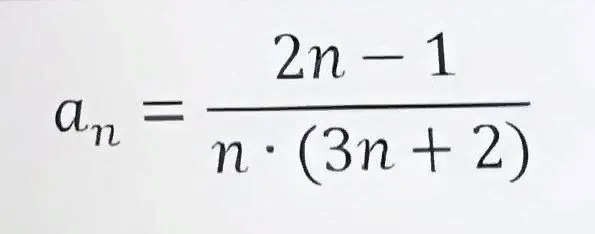 F)
F)
Решение. В каждую формулу вместо n подставим любое из чисел 1, 2, 3, 4.
Почему эти числа ? А потому что именно первые 4 члена данной последовательности нам известны.
Затем полученные результаты сравним с элементами ряда. При использовании каких формулах ответы совпадут, те и подойдут нам.
А) (2×2)-1))/(2×(2×2+2))=(4-1)/(2×(4+2))=3/12
3/12≠2/(3×5)
Формула не подходит.
В) 2/((2×2-1)×(2×2+1))=2/(3×5)
2/(3×5)=2/(3×5)
Формула подходит.
С) 2/(4×(2^2)-1)=2/(4×4-1)=2/(16-1)=2/15
2/15=2/(3×5)
Формула подходит.
D) 2/(2×(2×2+1))=2/(2×(4+1)=2/(2×5)=2/10
2/10≠2/(3×5)
Формула не подходит.
E) 3×2-2/(2×(3×2+2))=6-2/(2×8)=4/16=1/4
1/4≠2/(3×5)
Формула не подходит.
F) 2×2-1/(2×(3×2+2)=4-1/(2×(6+2)+3/24=⅛
1/8≠2/(3×5)
Формула не подходит.
Ответ: В, С.
Задания для самопроверки:
Задание 1
Определив закономерность, найдите чему равен х.
431 (21) 10
269 (17) 20
380 (х) 20
Задание 2
Установите закономерность и найдите неизвестный член.
{1, 5, 14, 30, 55, ?}
Задание 3
Шестой элемент последовательности {3, 5, 11, 29, 83…} равен…
Ответы:
1 – 20.
2 – 91
3 – 245.
