Показательная функция
Изучая разные виды функций и их графики, мы говорили о том, что среди них есть те, которые требует более детального рассмотрения. Одной из таких функций является показательная.
Показательные функции широко используются для описания и моделирования различных процессов роста и изменений в самых различных областях науки. Так что данная тема поможет не только хорошо написать ЕНТ, но и пригодится экономистам при изучении тенденций роста рынков и инвестиций, будет необходима IT-специалистам для описания экспоненциального роста объемов данных и производительности компьютеров, а также многим другим.
Показательная функция.
Функцию принято называть показательной, если она задана следующим уравнением: f(x)=a^x.
а — это основание, оно представлено заданным числом, которое остается постоянным, даже после того, как у нас меняется переменная х.
х — это все тот же аргумент (независимая величина.) В данном случае он является степенью нашего основания.
Легко можно понять, что функция получила свое название исходя из того, что х представляет собой ничто иное, как показатель функции.
Ограничения функции.
Когда мы выполняем задания с данным видом функции нам важно знать и помнить, что наше основание не может принимать любые значения. Существует определенные ограничения.
Во-первых, а≠1.
Наше основание не может быть равным единице потому что в таком случае при любом значении х наш у будет принимать значение единицы. Ведь 1 во всех возможных степенях так и останется 1.
Во-вторых, а>0.
Наше основание не должно быть равным нулю по той же самой причине, что и в ситуации с единицей.
Но почему а не может принимать отрицательные значения ? На самом деле все очень просто.
Представим, что наш х равен 1/2. Запишем это по-другому, учитывая, что степень равная 0,5 это корень квадратный. Тогда выйдет, что а^(1/2) = √а.
А теперь попробуете извлечь корень из -4 или -16. Если вы получили хоть один из данных ответов {2, -2, 4, -4}, то можете с гордостью получить свою заслуженную двойку. Потому что, запоминайте, из отрицательного числа нельзя извлечь корень.
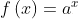

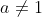

График показательной функции
Графики показательной функции можно разделить на две большие группы. Классификация происходит по значению основания.
К 1 группе относятся все функции, в которых основание больше единицы.
Ко 2 группе те функции, где основание больше нуля, но меньше единицы.
1) а > 1.
2) 0 < а < 1.
Давайте попробуем сделать таблицу и начертить графики для двух показательных функций. Для этого возьмём от каждой по 4 точки.
А) у=2^х
| х | -1 | 0 | 1 | 2 |
| у | 0,5 | 1 | 2 | 4 |
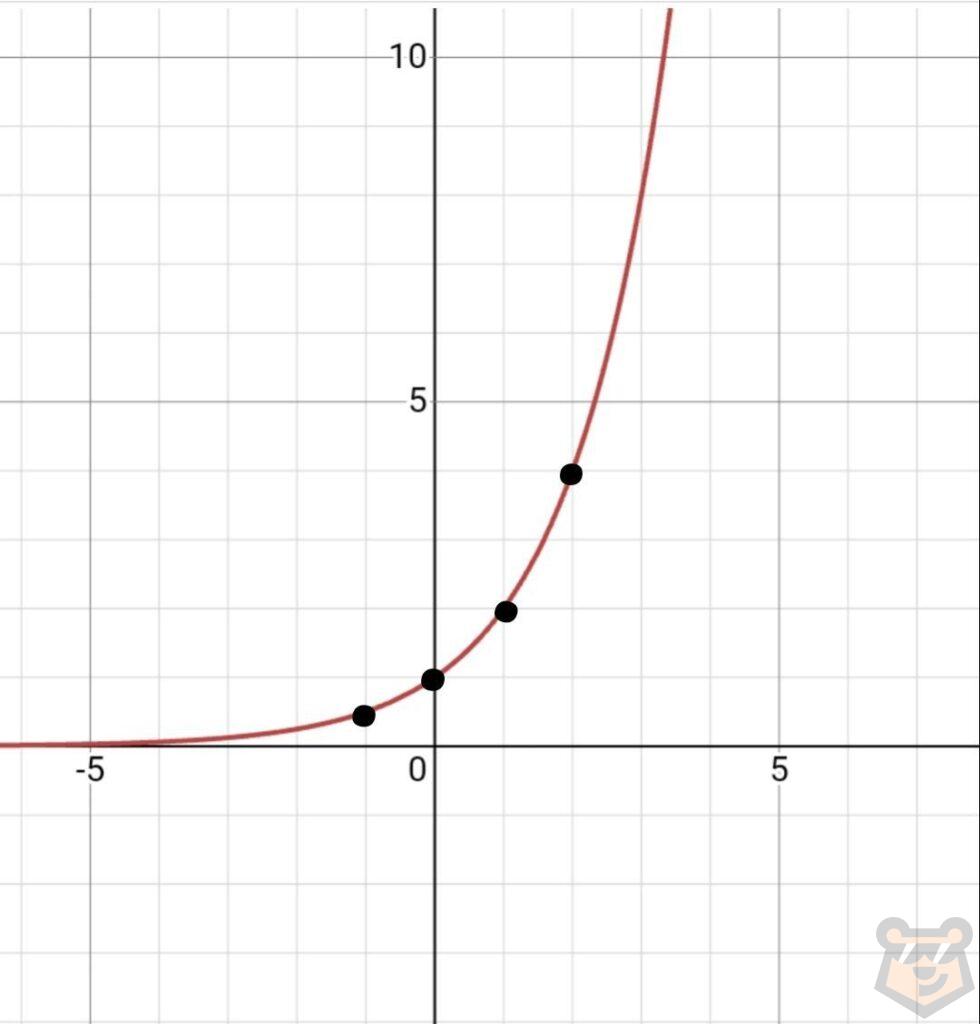
В) у=0,5^х
| х | -1 | 0 | 1 | 2 |
| у | 2 | 1 | 0,5 | 0,01 |
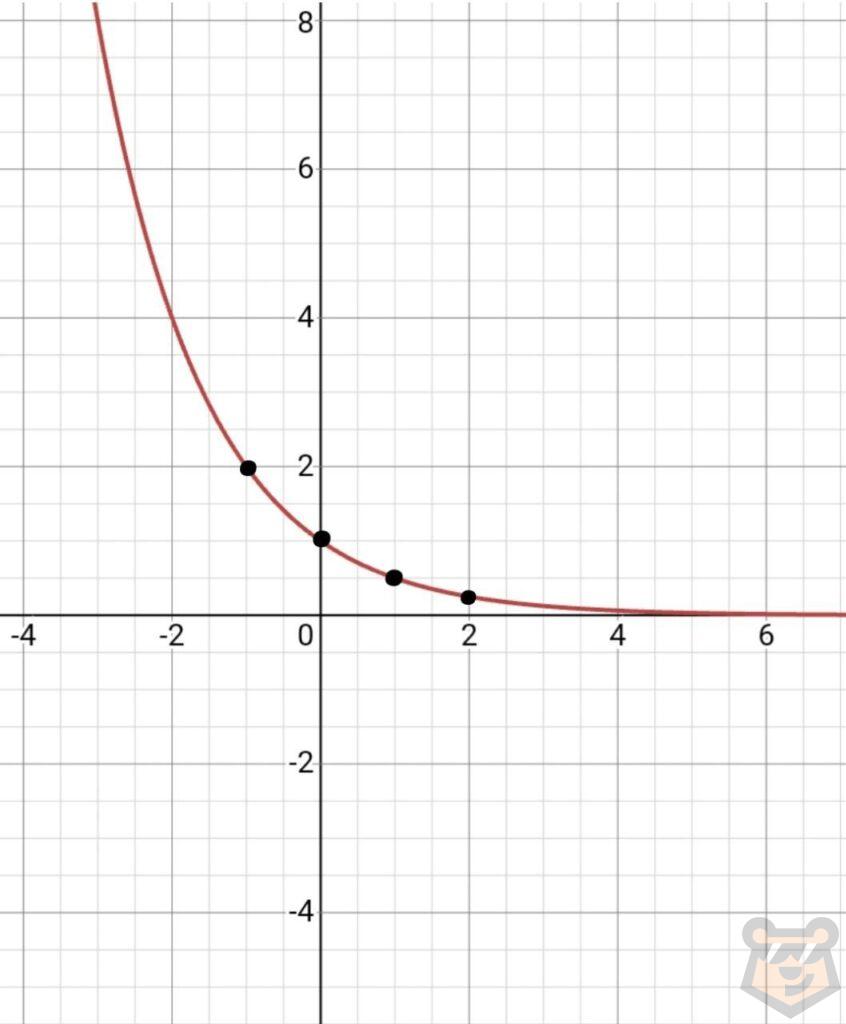
Посмотрев на наши графики мы понимаем, что они напоминают ветвь гиперболы.
Также можно заметить, что у каждой показательной функции есть своя асимптота. В двух данных случаях это прямая у = 0. Значение наших функций может стремиться к нулю, но никогда его не достигнет. Ведь какое бы мы число ни возвели в любую из всех существующих степеней мы никаким образом не сможем получить нуль.
| а > 1. | 0 < а < 1. |
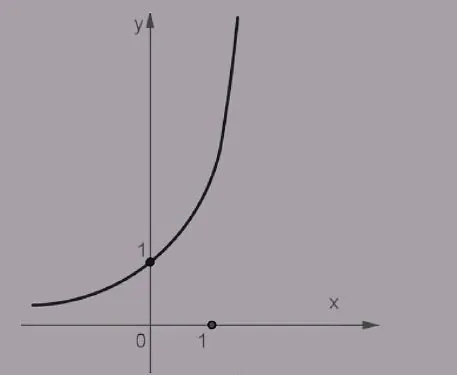 |  |
Постараемся это запомнить с помощью небольшой подсказки, основанной на одном достаточно известном меме.
| а > 1. | 0 < а < 1. |
 |  |
Область определения и область значений показательной функции
Смотря на наши графики и учитывая все ограничения нашего основания, можем легко понять область определения и область значений.
Вместо х мы в большинстве случаев можем подставить любое число. Таким образом, чаще всего область определений показательной функции (всевозможные х) это D (y)= (- ∞; + ∞).
До этого мы упоминали, что в основном асимптотой показательной функции является у = 0. Выходит, что при стандартном раскладе область значений функции (всевозможные у) это E (y) = (0 ; + ∞).
Практическая часть.
Задание №1. Проходит ли график функции заданной уравнением у = 4^х — 9 через точку А(4;55) ?
Решение. Вспоминаем, что координаты пишут в таком порядке (х;у). Тогда выходит, что х = 4, а у = 55. Подставим полученные значения в уравнение и проверим все ли сходится.
55 = 4^4 — 9
55 = 64 — 9
55 = 55.
Все сошлось. Значит данная точка принадлежит нашей функции.
Ответ: да, проходит.
Задание №2. Функция задана уравнением у = 4^х — 2. Найдите асимптоту данной функции. Затем вычислите чему будет равен у если нашим аргументом является 4.
Решение. А) Помним, что по стандартной записи у = а^х, асимптотой является 0. А в данном уравнение еще появляется -2. Значит вершина графика опускается на две единицы вниз. И в таком случае наш график будет стремиться не к нулю, а к минус двум (0-2=-2). Выходит, что нашей асимптотой будет у = -2.
В) Вычислим наш у при х = 4.
Просто необходимо подставить 4 на место х и посчитать.
у = 4^4 — 2 = 256 — 2 = 254
Ответ: у = -2, у = 254.
Задание по данному разделу, которые встречаются на ЕНТ.
Задания на тему «Показательная функция» на едином национальном тестировании присутствуют лишь в профильной математике. Типы встречающихся задач нельзя назвать сильно сложными, но для того, чтобы уж точно быть уверенными, что мы в силах их решить, рассмотрим несколько примеров.
Задание №1. Найдите область определения функции у = 3^(2 / (3х-3))
Решение. Обратим внимание на нашу степень, которая представлена дробью 2 / (3х-3). Вспомним, что на нуль делить нельзя. Значит 3х-3≠0. Решаем данное выражение.
3х≠3.
х≠3/3
х≠1.
В таком случае, наш аргумент может принимать любые значения, кроме единицы.
Ответ: D(y) = (- ∞; 1) ∪ (1; + ∞).
Задание №2. Найдите точки пересечения графика функции у=3^х-9 с осями координат.
Решение. Вспоминаем свойства функции.
Пересечение с осью ординат, когда у=0.
Пересечение с осью абсцисс, когда х=0.
Ось Оу. 3^х — 9=0
3^х = 9
3^х = 3^2
х = 2.
«Складываем» наши значения в координаты. (2; 0)
Ось Ох. у = 3^0 — 9
у = 1 — 9
у = -8
Получаем (0; -8).
Ответ: (2; 0), (0; -8).
Задание №3. Используя предоставленный график, составьте уравнение с помощью, которого можно найти точку пересечения данных двух функций.
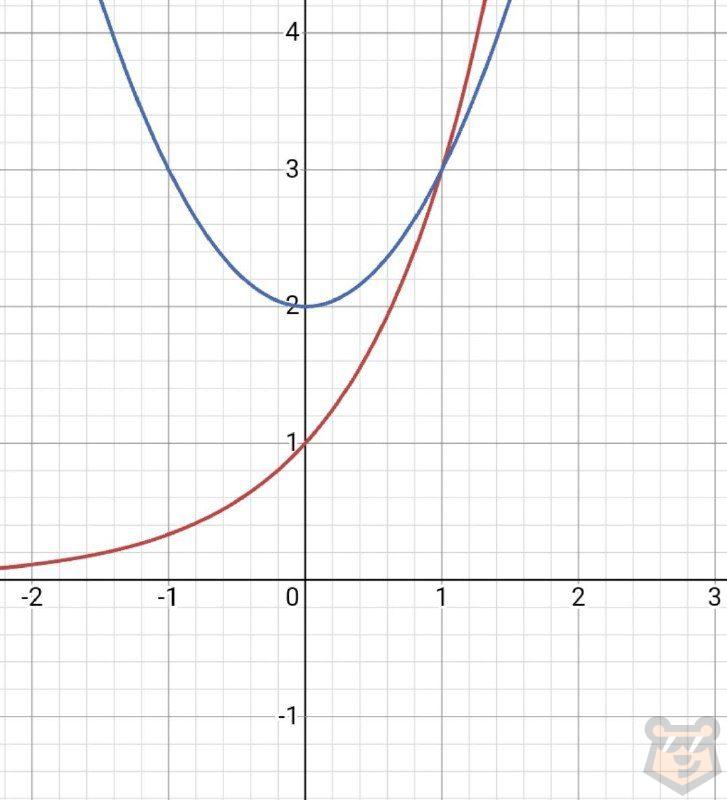
Решение. Во-первых, необходимо составить уравнения, которыми заданы наши функции.
А) Синяя функция это парабола.
Видим, что ее вершина на две единицы поднята от начала координат. Значит получим у = х^2 + 2.
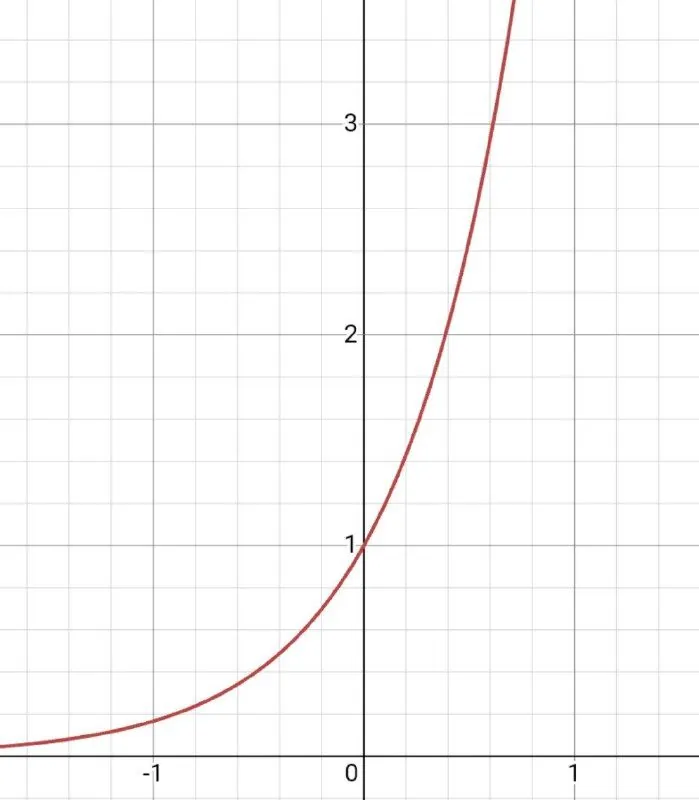
В) Красная функция это показательная функция.
Обратим внимание на то, что вершина функции ни на шаг не сдвинулась от начала координат. Значит ничего прибавлять или отнимать не надо. Выходит, что это стандартный вид показательной функции у=а^х.
Теперь посмотрим на значение нашей функции при аргументе, равном 1, у = 3.
(у = 3; х = 1)
Подставим наши значения в запись у = а^х.
3 = а^1
Получается, что а=3.
Значит функция задана уравнением у = а^3.
Во-вторых, находим уравнение для поиска точки пересечения. Для этого приравниваем одно уравнение к другому. х^2 + 2 = 3^х.
Ответ: х^2 + 2 = 3^х.
Задание №4. Вычислите чему равна переменная х, если значение функции, заданной уравнением f(x) = 2^х + 4 , равно 36.
Решение. Необходимо составить самое простое из всех возможных показательных уравнений. Оно будет выглядеть так: 2^х + 4 = 36.
Теперь решим его.
1. Сделаем так, чтобы значения с х и наши числа были по разные стороны знака «равно». Для этого перенесем 4 из одной стороны в другую. (Не забудьте поменять знак на противоположный!)
2^х + 4 = 36
2^х = 36 — 4
2^х = 32
2. Представим 32 как двойку в пятой степени.
2^х = 2^5
3. Смотрим внимательно на наше равенство и делаем вывод, что х=5.
Ответ: 5.
Задание №5. Даны три функции: у = 0,4^х, у = 2^х + 1, у = 6^х. Сопоставьте графики данных функций с их уравнениями.
| 1 |
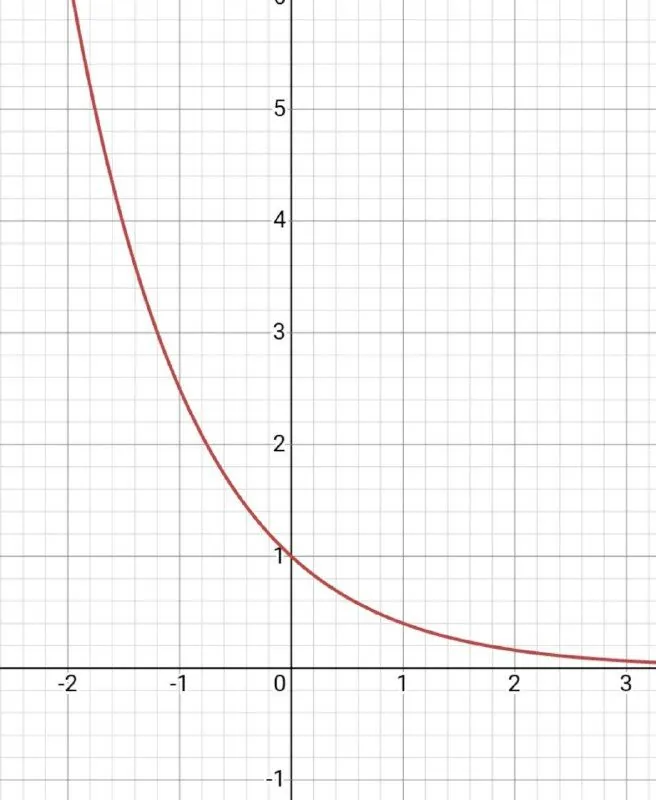 |
| 2 |
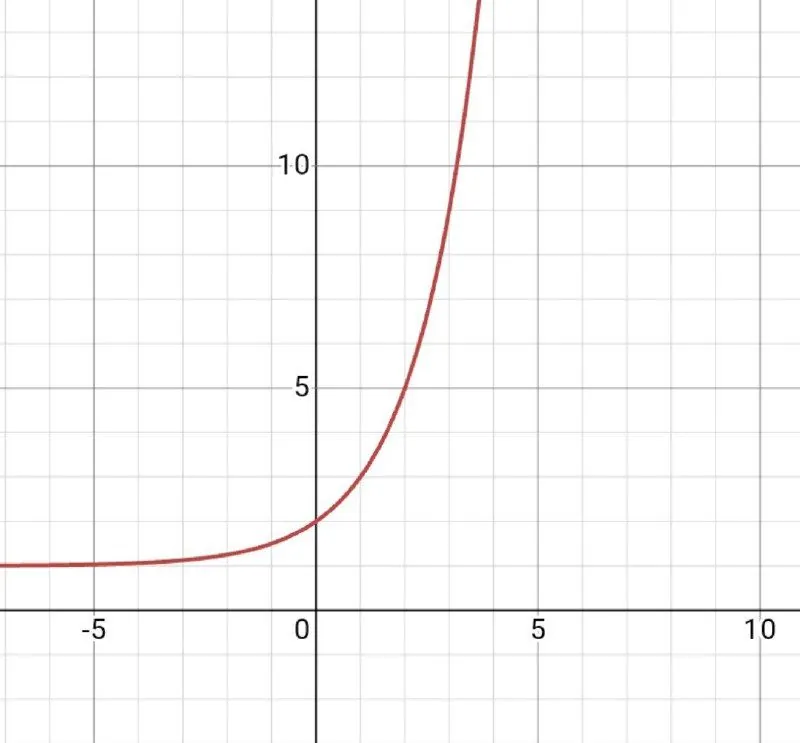 |
| 3 |
 |
Решение. А) у = 0,4^х. Вспомним как выглядит график функции, у которой основание характеризуется следующим неравенством 0<а<1. И тогда с легкостью поймем, что график функции у=0,4^х находится под цифрой 2.
В) у = 2^х + 1. У нас к стандартной записи добавили + 1. Значит, необходимо найти график, у которого асимптотой будет у = 1. Видим, что подходящий график находится под номером 1.
С) у = 6^х. Данный график уже можно найти методом исключения. Или же можно обратить внимание на то, что у нас стандартная запись показательной функции, у которой а>1 и асимптотой является у = 0. Выходит, что нужный нам график расположен под цифрой 3.
Ответ: 1 — у = 2^х + 1; 2 — у=0,4^х; 3 — у = 6^х.
Задания для самопроверки:
Задание 1
Найдите область определения и область значений функции, заданной уравнением у = 6^(4/(х+3))
Задание 2
Определите координаты точек, где функция у = 3^х + 3 и оси координат пересечения.
Задание 3
Функция задана уравнением у=3^х +5. Найдите аргументы, при которых значение функции равно 248, 32, 8.
Ответы:
1 – D(y) = (- ∞; -3) ∪ (-3; + ∞), E(y) = (0; +∞).
2 – (0; 4).
3 – 5, 3, 1.
