Логарифмическая функция
Логарифмическую и показательную функции привыкли считать двумя эдакими подружками, даже несмотря на то, что у них есть некоторые отличия. Поэтому изучив одну из них, сразу же приступают к другой. Все потому что таким образом будет намного легче усвоить весь необходимый материал по данным темам. Вы сами еще в этом успеете убедиться.
И так, логарифмическая функция, как и показательная применяется в самых различных областях. Например, в физике, в химии, в экономике. Применение такому виду функции нашли и в работе с информационными технологиями. Ведь логарифмическая функция позволяет упрощать сложные математические выражения и делает процесс их решения менее трудным и более быстрым. Кроме того эта функция встречается в задачах на едином национальном тестировании. Поэтому крайне не советуем вам пропускать данную тему.

Логарифмическая функция
Логарифмическая функция — это математическая функция, заданная следующим уравнением:

log — это, естественно, сам логарифм.
х — это наш аргумент.
а — это наше основание, оно представлено числовым значение и остается постоянным даже при изменении х.
Из самого названия функции мы понимаем, что она тесно связано с понятием «логарифм» и с основными свойствами логарифма. Поэтому прежде чем приступить к изучению этой функции стоит ознакомиться с вышеперечисленными темами.
Ограничения логарифмической функции
Вспоминая свойства логарифма, можно легко сделать вывод, что наше основание не может принимать абсолютно любое значение. Поэтому существуют определенные границы.
Во-первых, основание не должно быть равно единице.
Потому что мы знаем, что единица в какую степень ее не возведи, так и останется единицей. Поэтому смысла ставить ее в основание просто-напросто нет.
Во-вторых, основание должно быть больше нуля.
Основание не может быть равно нулю по той же причине, что и в ситуации с единицей.
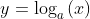

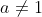

График логарифмической функции
Графики логарифмических функций можно разделить на две большие группы. Классификация происходит по значению основания.
К первой группе относятся функции, основания которых больше единицы.
Ко второй группе относят те функции, у которых основание больше нуля, но меньше единицы.
| 1 группа | 2 группа |
| а>1 | 0<а<1 |
Давайте разберем два примера и определим чем же отличаются графики разных групп. Для того чтобы начертить график, возьмем по три точки от каждой функции.
А)
| х | 1 | 2 | 4 |
| у | 0 | 1 | 2 |
у = log 2 ¹
y = 0
у = log 2 ²
y = 1
у = log 2 ⁴
y = 2
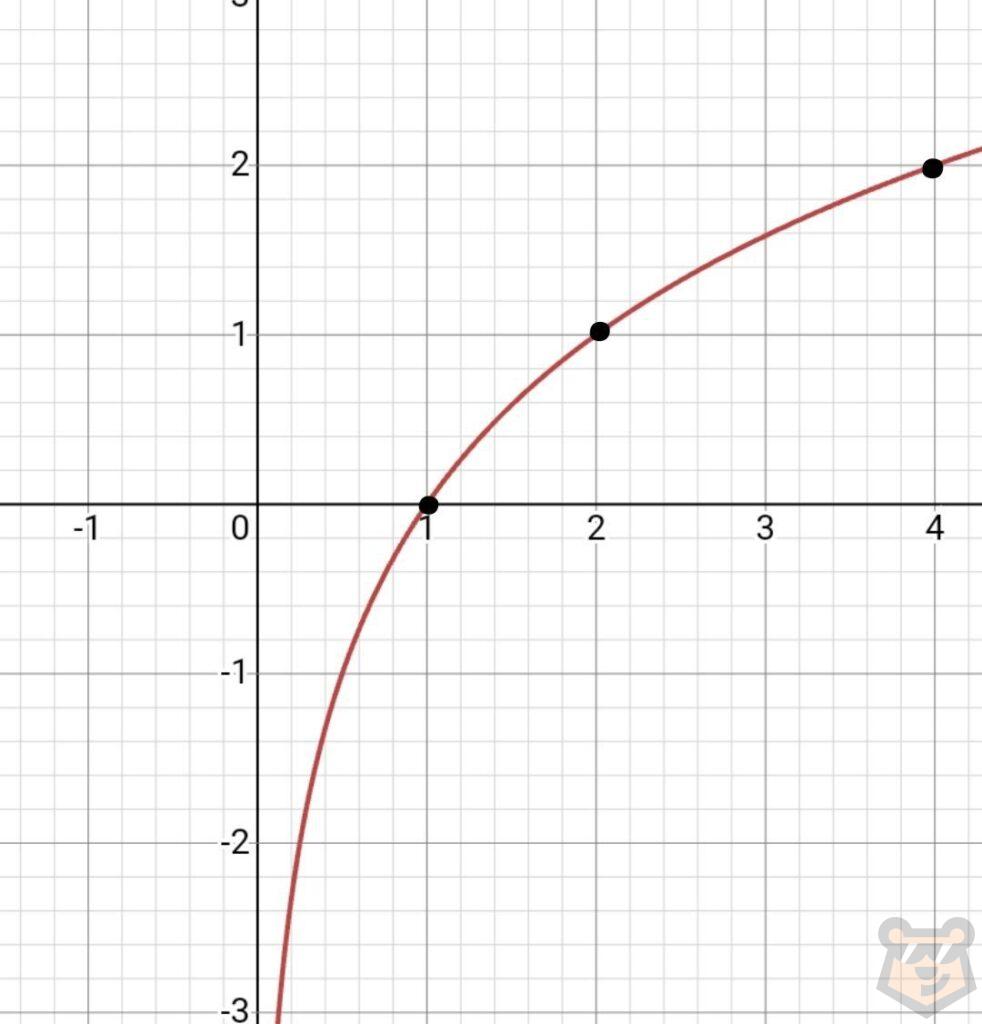
В)
| х | -2 | -1 | 1 |
| у | 4 | 2 | 0 |
у = log 0,5 ¯²
y = 4
у = log 0,5 ¯¹
y = 2
у = log 0,5 ¹
y = 0
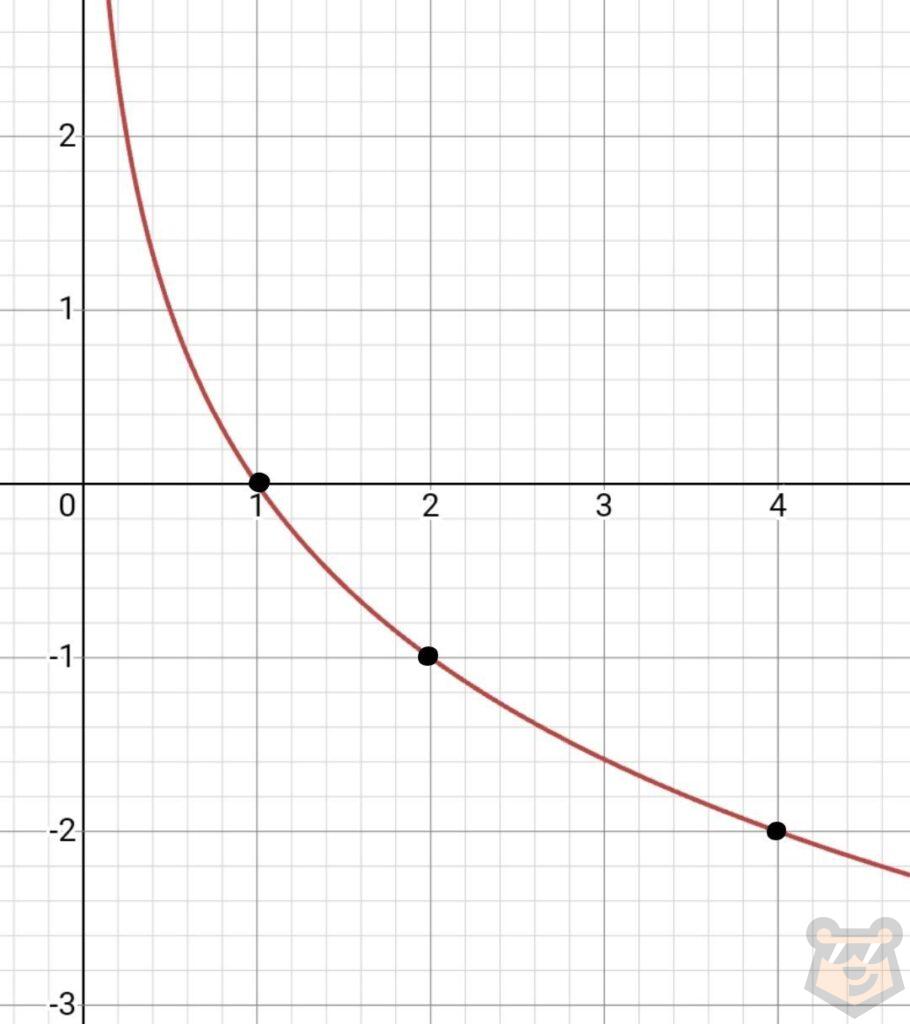
Помимо явных отличий между графиками двух разных групп можно заметить, что у логарифмической функции есть асимптота, которой является прямая х=0.
Почему же так ? Давайте попробуем вместе разобраться.
Для того чтобы значение логарифма было равно нулю нам необходимо в основание поставить нуль. Потому что только нуль в любой степени будет нулем. Остальные числа лишь смогут приблизиться к такому значению, но никогда его не достигнут. Однако ранее было сказано, что в основание нельзя ставить нуль, ведь иначе это будет противоречить свойствам логарифмической функции и логарифма в целом. Именно поэтому логарифмическая функция будет лишь стремиться к нулю.
| а>1 | 0<а<1 |
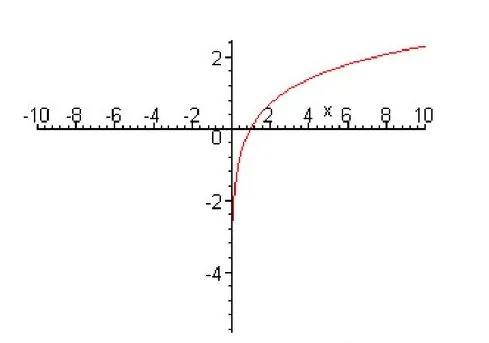 | 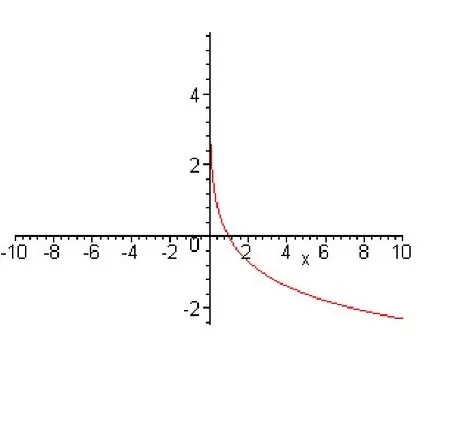 |
Запомним как выглядят графики логарифмических функций с помощью небольшой таблицы с бумерангами.
| а>1 | 0<а<1 |
 |  |
Область определения и область значений логарифмической функции
Смотря на наши графики и учитывая все ограничения нашего основания, можем легко понять область определения и область значений.
Вместо х согласно свойству логарифма (основание должно быть больше нуля) мы можем поставить только положительные числа. Таким образом, область определений логарифмической функции (всевозможные х) это D (y)= (0 ; + ∞).
А область значений функции (всевозможные у) это E (y) = (- ∞; + ∞).
Логарифмическая и показательная функции
Думаю, самые внимательные и смышленые юные математики смогли заметить, что показательная функция и логарифмическая взаимообратные.
Потому что у = а^х и у = loga x это две противоположные вещи, как производная и первообразная, как умножение и деление, как плюс и минус.
Это можно легко запомнить благодаря прекрасной ассоциации с двумя героями из известного мультсериала «Аватар: легенда об Аанге». Этими героями будут Катара и Зуко, олицетворяющие две противоположные стихии — вода и огонь.
Практическая часть.
Задание №1. Принадлежит ли точка (27;4) функции, заданной уравнением у=log3 x ?
Решение. Учтем то, что координаты принято писать в таком порядке (х;у). Тогда выходит, что х = 27, а у = 4. Подставим полученные значения в уравнение у=log3 x и проверим все ли сходится.
4 = log3 ²⁷
log3 ²⁷ = 3
4 ≠ 3
Значения не сошлись. Выходит, что наш график не проходит через данную точку.
Ответ: нет, не принадлежит.
Задание №2. Дана функция у = log8 x. Найди чему равняется аргумент, если значение у равно 3.
Решение. Получается, нам необходимо сделать подобного рода запись. 3 = log 8x. И тогда мы должны решить одно из самых легких логарифмических уравнений.
Можем легко преобразовать логарифм и представить это так: 8^3 = х
В итоге наш х равен 512.
Ответ: 512.
Задания по данному разделу, которые встречаются на ЕНТ.
Задания на тему «Логарифмическая функция» на едином национальном тестировании присутствуют только в профильной математике. В целом типы встречающихся задач нельзя назвать сильно сложными. Но все же давайте посмотрим как правильно их решать.
Задание №1. Функция задана уравнением у = log 0,25 (3-x) . Найдите область определения данной функции.
Решение. Вспомним, что аргумент нашего логарифма должен быть положительным, то есть больше нуля. Тогда мы получим следующее неравенство.
3 — x > 0.
Решим данное неравенство. Для этого перенесем наш х за знак «больше».
(Не забывайте при переносе менять знаки на противоположные!)
3 > х
Можно это представить более привычным способом. х < 3
Выходит, что наш х может принимать все значения стоящие до тройки.
Ответ: D (y) = (- ∞; 3).
Задание №2. Укажите какие из 6 нижеперечисленных функций являются возрастающими, а какие являются убывающими.
А) y = log0,2 x
В) y = log0,7 (x — 3)
С) y = log3 x
D) y = log16 (x + 4)
E) y = log√0,64 (3x)
F) y = log√(1/0,25) x
Решение. Для решения задачи необходимо рассматривать каждую функцию отдельно. Вернее сказать, будем внимательно рассматривать наши основания. Потому что если обратить внимания на наши графики, то при основании, которое больше единицы, согласно свойствам функции, график растет. А вот функции с основанием, принадлежащем промежутку (0; 1), наоборот убывают. Поэтому давайте учитывая это, начнем решать задание.
А) y = log0,2 x
а = 0,2 0 < 0,2 < 1 Значит функция убывающая.
В) y = log0,7 (x — 3)
а = 0,2 0 < 0,7 < 1 Значит функция убывающая.
С) y = log3 x
а = 3 3 > 1 Тогда функции возрастающая.
D) y = log16 (x + 4)
а = 16 16 > 1 Тогда функции возрастающая.
E) y = log√0,64 (3x)
а = √0,64 = 0,8 0 < 0,8 < 1 Значит функция убывающая.
F) y = log√(1/0,25) x
а = √(1/0,25) = √4 = 2 2 > 1 Тогда функции возрастающая.
В итоге получим: А — убывающая;
В — убывающая;
С — возрастающая;
D — возрастающая;
E — убывающая;
F- возрастающая;
Ответ: убывающие — А, В, Е; возрастающие — С, D, F.
Задание №3. Логарифмическая функция задана уравнением у=log0,5 (3x-2). Определите наименьшее и наибольшее значение функции на промежутке [1; 10/3].
Решение. Для начало найдем ОДЗ нашего логарифма. Помним, что аргумент должен быть больше нуля. Тогда получим следующее неравенство: 3х-2 > 0
Решим данное неравенство.
3х > 2
х > 2/3
2/3 ≈ 0,67
Наш промежуток больше данного значения. Значит, мы можем не беспокоиться, что некоторые числа нельзя будет подставить.
Теперь определим какие значения входят в наш промежуток.
10/3 ≈ 3.3 В таком случае у нас интервал от 1 до 3.3.
Давайте попробуем подставить наше первое и наше последнее значения.
х = 1
у = log0,5 (3×1 — 2) = log0,5 (3 — 2) = log0,5 1 = 0
х = 10/3
у = log0,5 (3×10/3 — 2) = log0,5 (10 — 2) = log0,5 8 = -3
Можно для проверки еще подставить 2.
х = 2
у = log0,5 (3×2 — 2) = log0,5 (6 — 2) = log0,5 4 = -2
Тогда получается, что минимальное значение на данном нам отрезке это -2, а максимальное значение это 0.
Ответ: наименьшее – -2, наибольшее – 0.
Задание №4. Найдите точку, где ось абсцисс пересекается с графиком функции, которая задана уравнением у = log0,25 (x + 2).
Решение. Вспоминаем свойства функции. Пересечение с осью Ох происходит, когда наш у равняется нулю. В таком случае нам необходимо наше уравнение проверять к нулю. А после сделать все необходимые вычисления.
log0,25 (x + 2) = 0
Учитывая то, что любое число в нулевой степени равняется единице, представим наш нуль в правой стороне как логарифм от 1 по основании 0,25.
log0,25 (x+2) = log0,25 1
Теперь уберем наш логарифм с его основанием.
x + 2 = 1
х = 1 — 2
х = -1
Запишем наши координаты с учетом того, что х = -1, а у=0. (-1; 0)
Ответ: (-1; 0).
Задания для самопроверки:
Ниже представлено несколько заданий для самостоятельного решения. Проверьте насколько хорошо вы запомнили и усвоили изученный материал.
Задание 1
Функция задана уравнение у= loga (x+3). Определите чему равно основание логарифма, если известно, что при аргументе, равном 340, значение функции равняется 3.
Задание 2
Найдите область определения логарифмической функции, если она задана уравнением у = log0,24 √(x+0,36)
Задание 3
Определите координаты точки, где график функции у = log0,25 (x+2) пересекается с осью ординат.
Ответы:
1 – 7.
2 – (-0,36; + ∞).
3 – (0, -1/2).
