Треугольники
Одной из самых обширных областей математики является планиметрия. Планиметрия — это такой раздел, который изучает фигуры, лежащие на плоскости. Получается, планиметрия включает в себя только те фигуры, которые имеют лишь длину и ширину.
Естественно, достаточно объемной частью планиметрии являются различные треугольники. Тема «Треугольник» начинается с вида данных фигур и заканчивается теоремой косинусов. Одним словом говоря, теоретический материал просто огромный, и самое важное, чертовски необходимый для хороших баллов на едином национальном тестировании. Поэтому прежде чем приступить к изучению советуем запастись терпением, нервами, носовыми платочками и сладким.
Что такое треугольник ?
Треугольники — это такие плоские фигуры, которые образуются при соединении трех точек, не лежащих на одной прямой.
Слово «треугольник» произошло от словосочетания «три угла». Следовательно, у данных фигур есть три угла. Помимо этого у них три стороны и три вершины.
Поработаем с одним чертежом.
*Стоит сразу обратить внимание, что чаще всего треугольникам дают название АВС.
Стороны треугольника — это и есть образующие его отрезки.
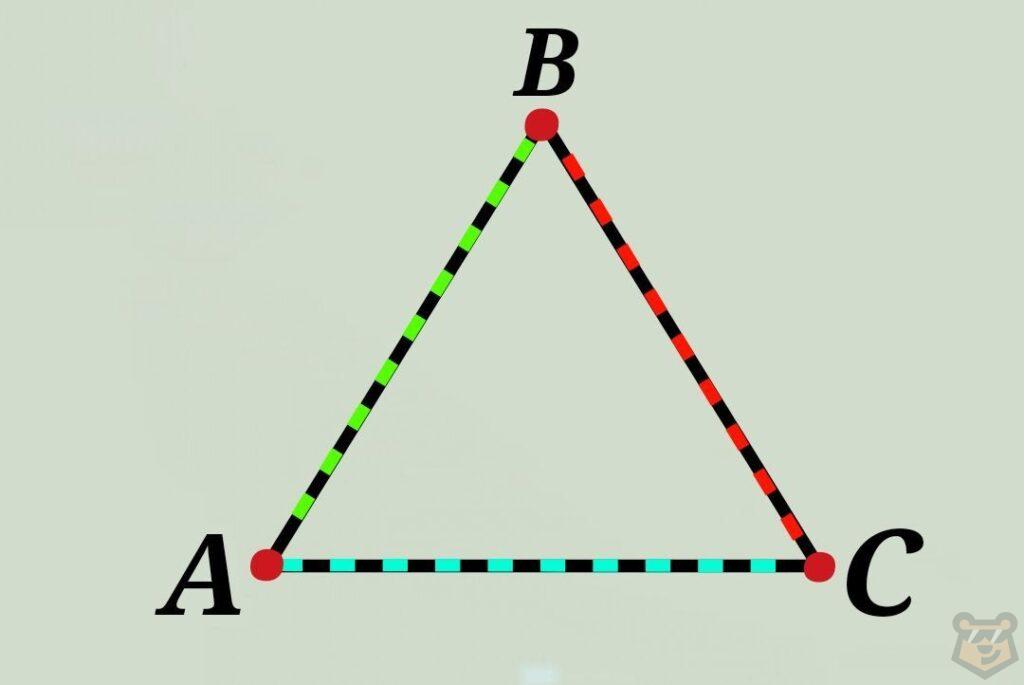
В данном случае это АВ, ВС и АС.
Вершина треугольника — это точка соединения двух его сторон.
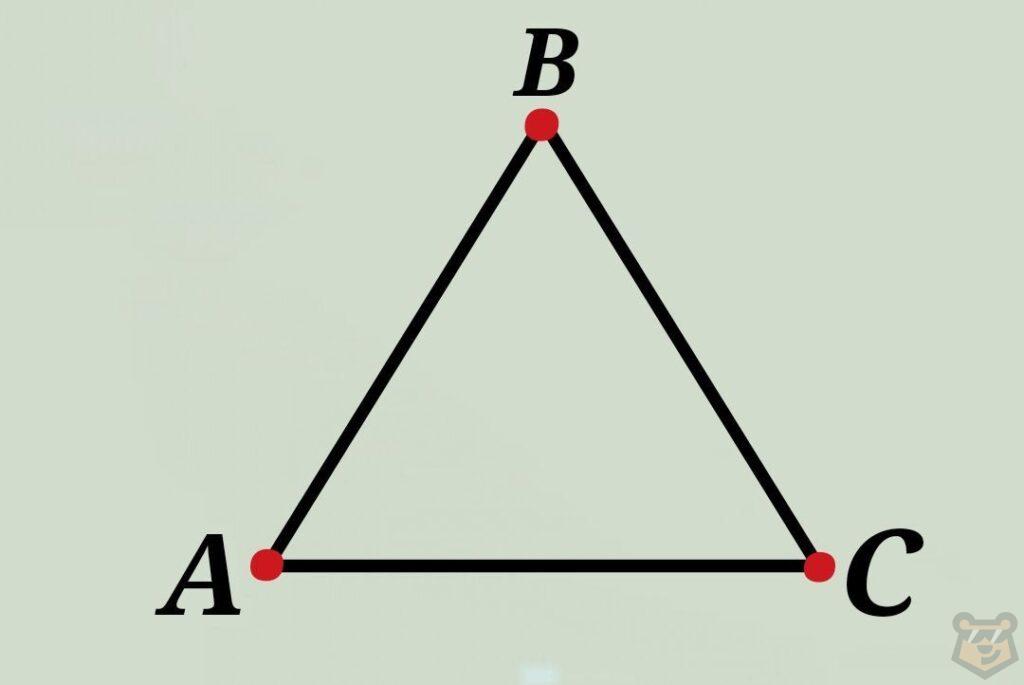
Вершинами являются точки А, В и С.
Угол треугольника — это угол, который находится между двумя сторонами.
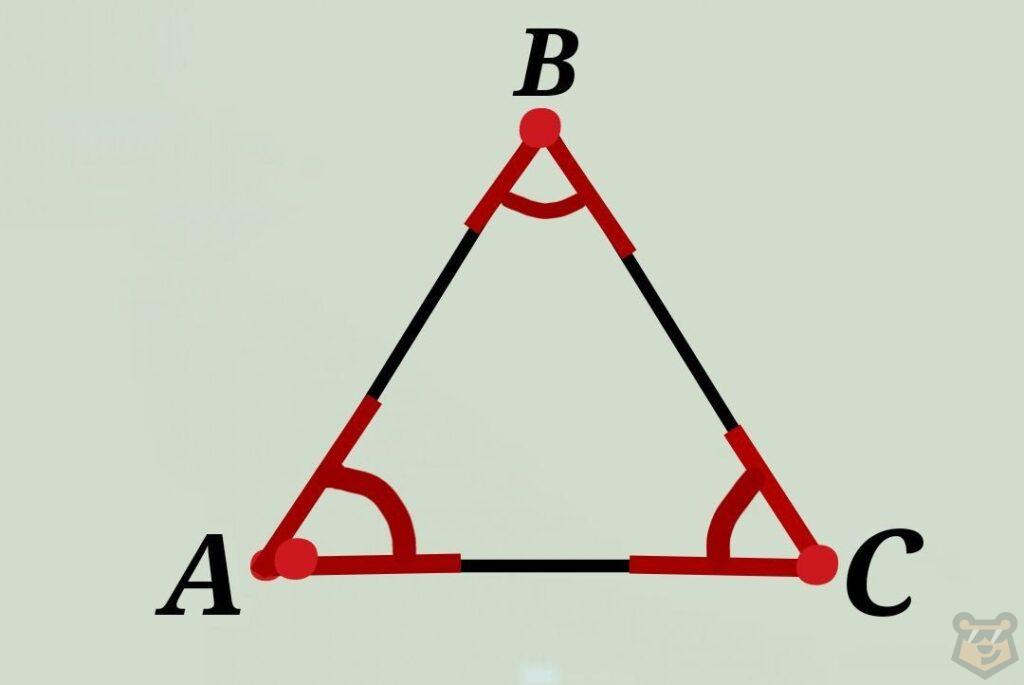
В нашем случае углы таковы: ∠АВС, ∠ВСА, ∠САВ. Также необходимо сказать, что углы можно обозначать и одной буквой. Например, ∠В это то же самое, что и ∠АВС.
Длины сторон.
Необходимо запомнить, что сумма длин двух сторон всегда будет больше длины третьей стороны. АВ + ВС > АС
Это теорема распространяется на все виды треугольников и никогда не должна нарушаться. Ведь вы никаким образом не сможете начертить треугольник так, чтобы его стороны были равны 30, 10 и 15. Как только не попробуйте изощряться, у вас все равно ничего не получится. Поэтому запомните, что даже наибольшая сторона должна быть меньше, чем сумма двух других.
Сумма внутренних углов треугольника.
Сумма трех внутренних углов треугольников при любом раскладе будет равна 180 градусам. ∠А + ∠В + ∠С = 180°
Допустим, нам необходимо начертить треугольник, у которого один угол будет равен 65 градусов, а другой — 70. В такой фигуре третий угол будет железобетонно равен 45 градусов. Потому что если от 180 градусов данные два угла отнять, то мы получим 45.
180° — 65° — 70° = 45°
Но когда кто-то постарается начертить треугольник с данными нам углами, у которого третий угол будет больше или меньше 45 градусов, то он потерпит сокрушительное поражение. Ведь это просто-напросто невозможно.
Сумма внешних углов треугольника.
Сумма внешних углов треугольника всегда равняется 360 градусам.
Почему именно такое значение ? Потому что внешние углы это ни что иное, как смежные углы со внутренними.
Напоминание ! Смежные углы — это углы, составляющие в сумме 180°.
Таким образом, три пары смежных углов в сумме равны 540 градусам. Теперь от данного значения отнимаем внутренние углы(180°), и получим 360 градусов.
540° — 180° = 360°.
Длины сторон и углы.
Взаимосвязь значения углов со сторонами фигуры можно выразить в двух простых предложениях. Их нужно запомнить.
Напротив большей стороны находится больший угол.
Напротив меньшего угла расположена наименьшая сторона.
Виды треугольников.
Существуют самые различные треугольники. На группы их классифицируют по длинам сторон и по углам.
Давайте для начала выделим типы фигур, отличающиеся углами. Для этого вспомним какие есть углы.
Углы.
1) Острый угол — это угол, градусная мера которого меньше 90°.

2) Тупой угол — это угол, который больше 90°.
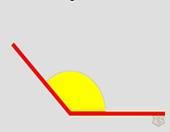
3) Прямой угол — это угол, равный 90°.
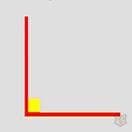
4) Развернутый угол — это угол, равный 180°.
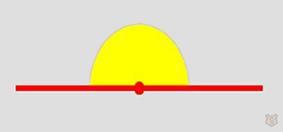
*Можно легко понять, что треугольников с развернутым углом не существует. Ведь сумма трех углов должна быть равной 180 градусам, а один развернутый угол это уже все 180.

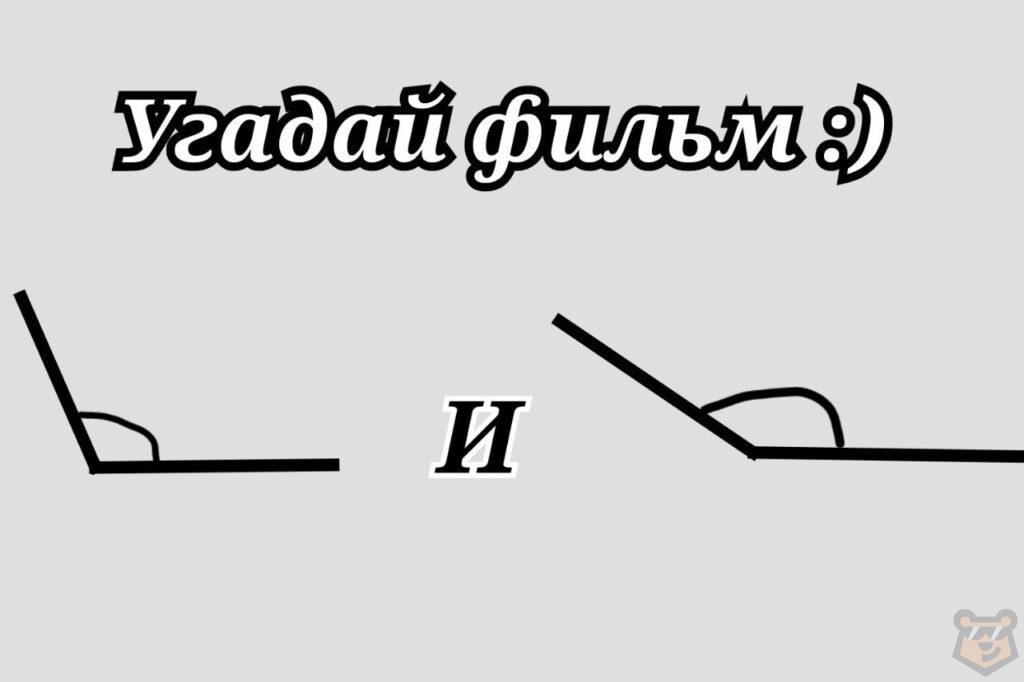
Виды треугольников в зависимости от углов.
Остроугольные треугольники.
Это такие треугольники, где все три угла являются острыми.
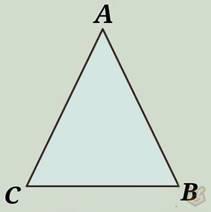
Тупоугольные треугольники.
Для данных фигур характерно иметь один тупой угол.
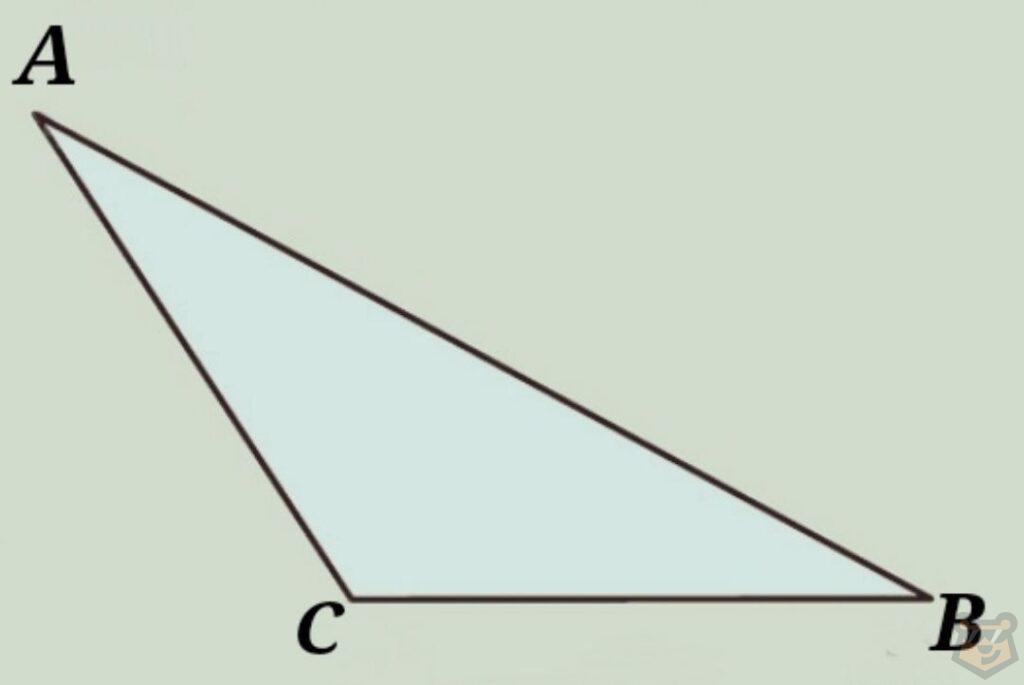
Прямоугольные треугольники.
Это треугольники, у которых есть один прямой угол.
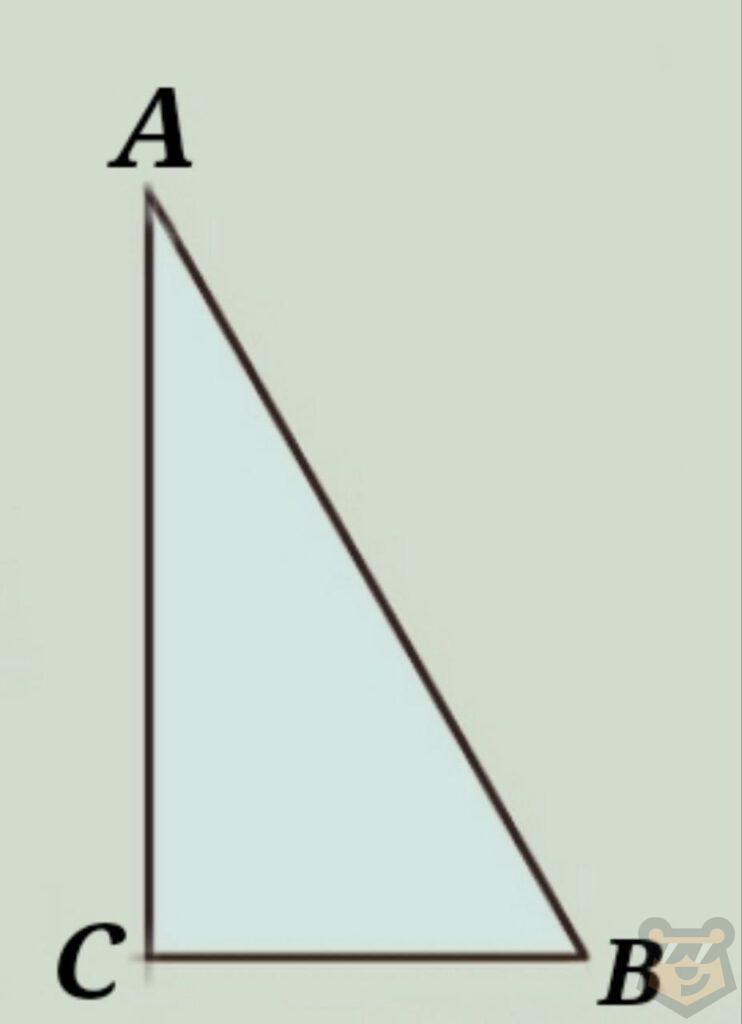
∠С = 90°
Стороны, которые образуют прямой угол, называются катетами.
Сторона, которая лежит напротив прямого угла, называется гипотенузой.
АС и СВ — катеты, АВ — гипотенуза.
Сумма острых углов между гипотенузой и каждым катетом равна 90 градусов.
∠А + ∠В = 90°
Длина катета, расположенного напротив угла в 30 градусов равна длине гипотенузы, деленной на два.
∠А = 30° Выходит, что СВ = АВ / 2
Виды треугольников в зависимости от сторон.
Разносторонние треугольники.
У данных треугольников все три стороны имеет разные длины.
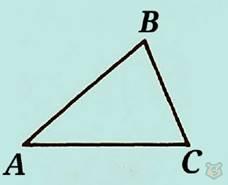
Равнобедренные треугольники.
Это треугольники, у которых две стороны равны.
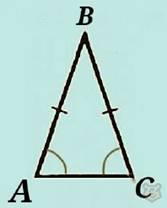
АВ = ВС
Равные стороны равнобедренного треугольника принято называть боковыми.
А третья сторона, отличающая по длине, является основанием.
АС и СВ — боковые стороны.
АВ — основание.
Также важно знать, что углы между основанием и каждой боковой стороной равны.
∠А = ∠С
Равносторонние треугольники.
Это такие треугольники, у которых все три стороны равны.
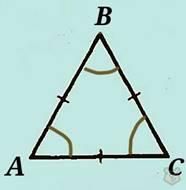
АВ = ВС = СА
Все стороны принято называть основаниями.
Все три угла таких треугольников равны между собой и составляют 60 градусов.
∠А = ∠В = ∠С = 60°
С учетом того, что у данного вида треугольника все стороны и углы равны, его еще также называют правильным.

Периметр треугольников.
Все мы знаем, что периметр — это сумма всех сторон. Таким образом, для того чтобы найти периметр треугольника нам необходимо сложить длины трех его сторон.
Р = АВ + ВС + СА
Равенство треугольников.
Два треугольника, как и любые другие фигуры, могут быть равны между собой. Для того чтобы понять равен ли один треугольник другому, необходимо знать признаки равенства треугольников.
I признак. Если две стороны и угол между ними одного треугольника равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.
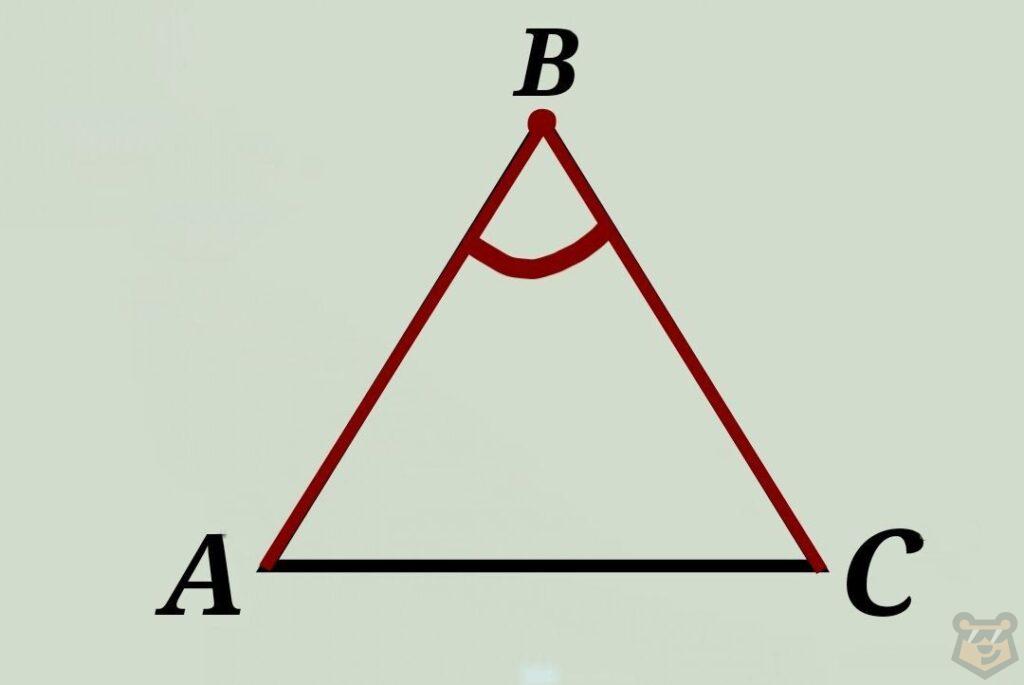
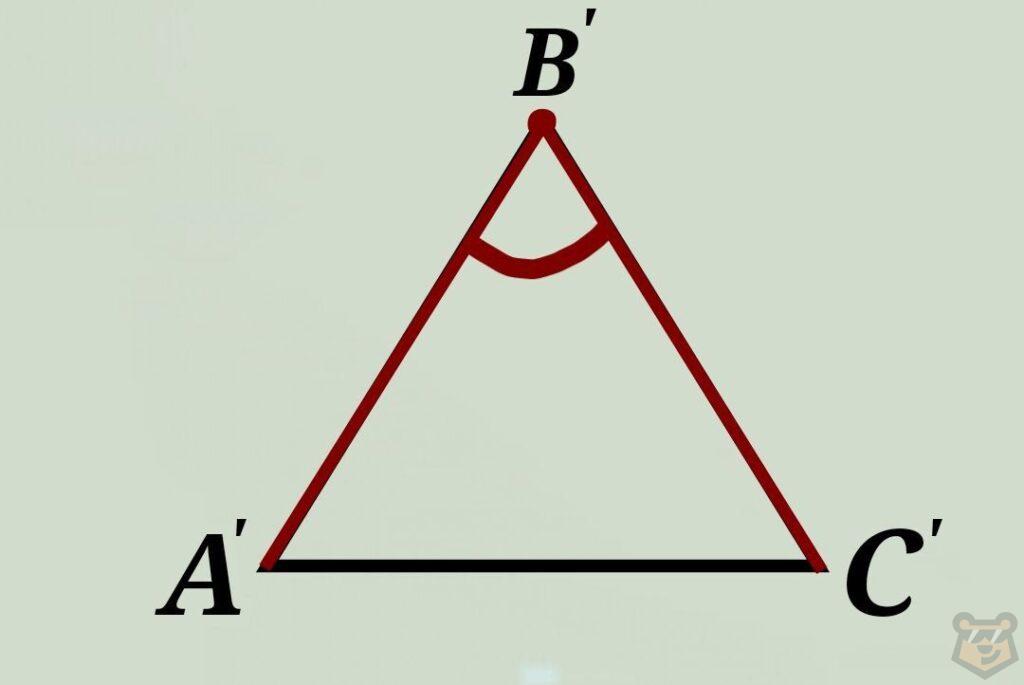
∆АВС = ∆А’В’С’, если АВ = А’В’; ВС = В’С’ и ∠В = ∠В.
II признак. Если сторона и два прилежащих к ней угла одного треугольника равны двум углам и соответствующей им стороне другого треугольника, то такие треугольники равны.
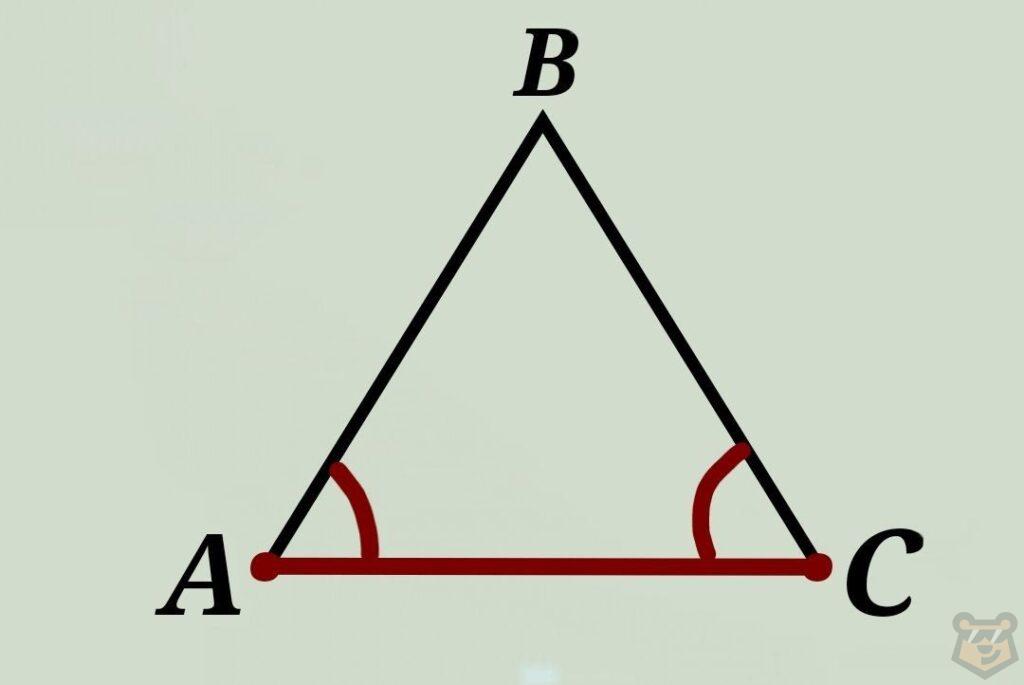
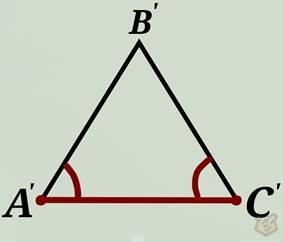
∆АВС = ∆А’В’С’, если АС=АС; ∠А = ∠А’ и ∠С = ∠С’.
III признак. Если три стороны одного треугольника равны трем сторонам другого треугольника, то такие треугольники равны.
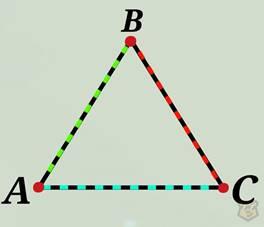
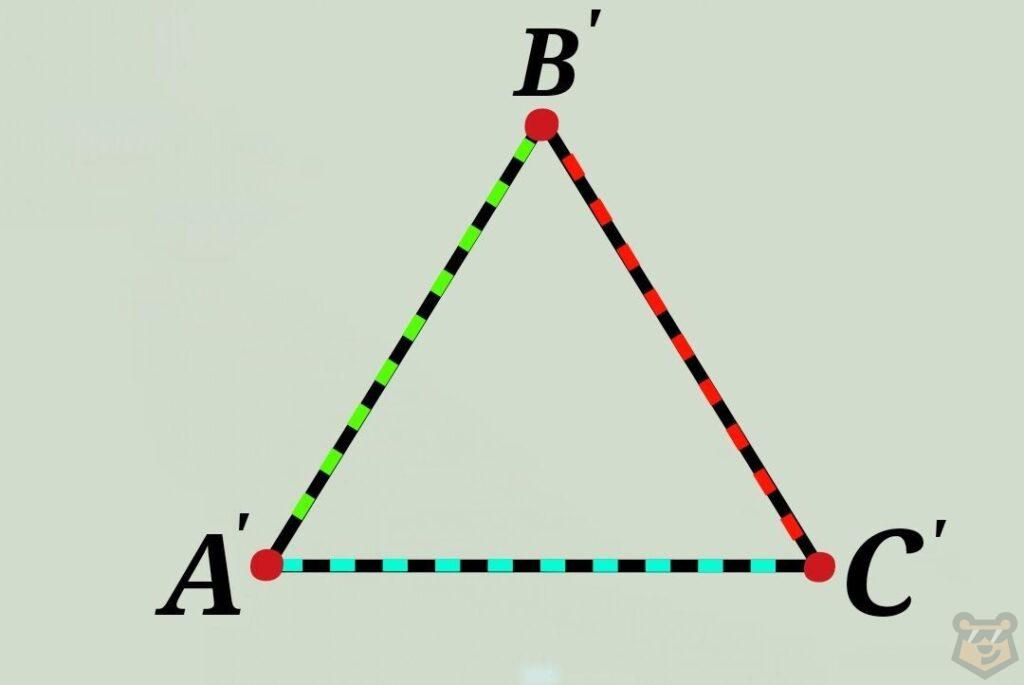
∆АВС = ∆А’В’С’, если АВ = А’В’; ВС = В’С’; СА=С’А’
Равенство прямоугольных треугольников.
1) Два прямоугольных треугольника равны, если катеты одного из них равны катетам второго.
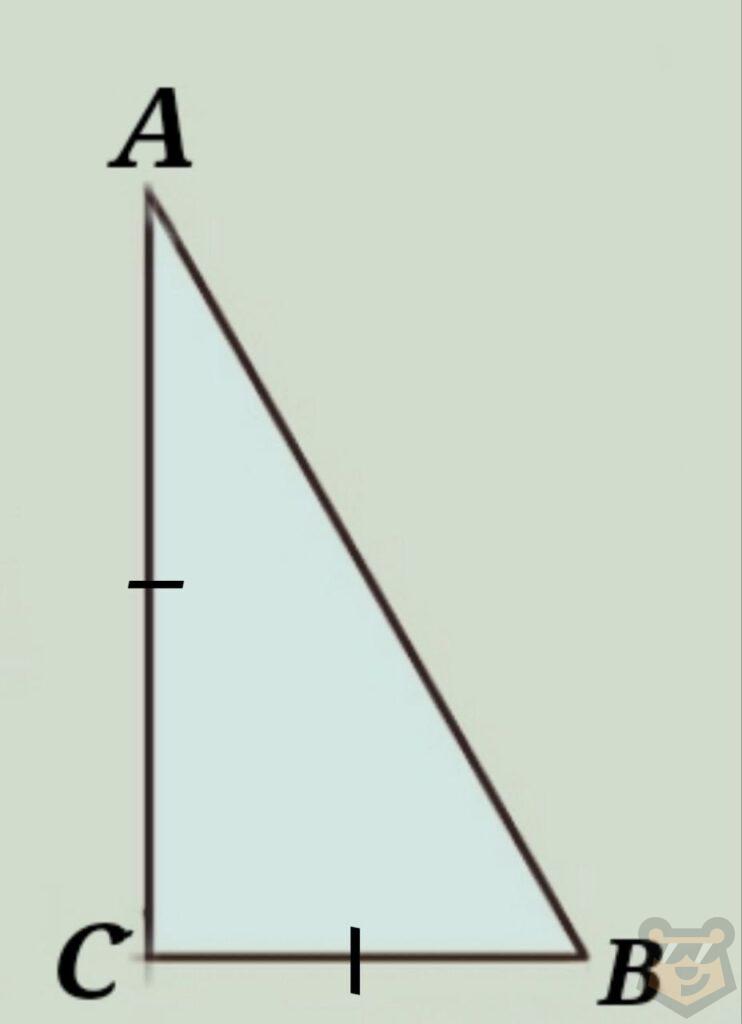
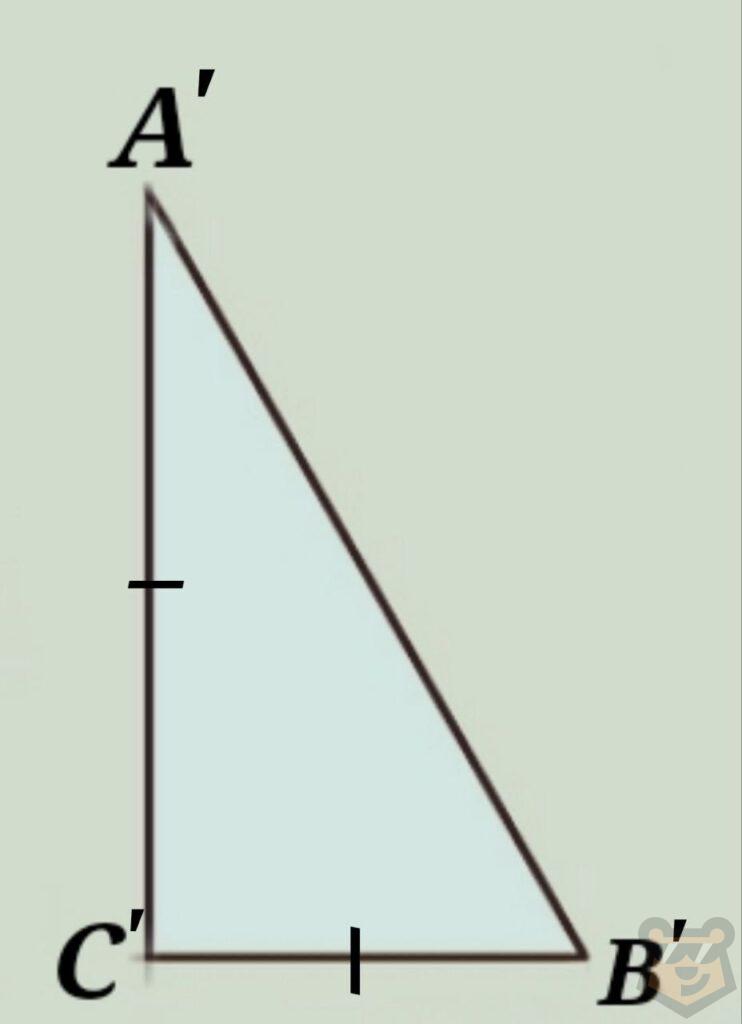
2) Два прямоугольных треугольника равны если гипотенуза и катет одного из них равны гипотенузе и катету второго.
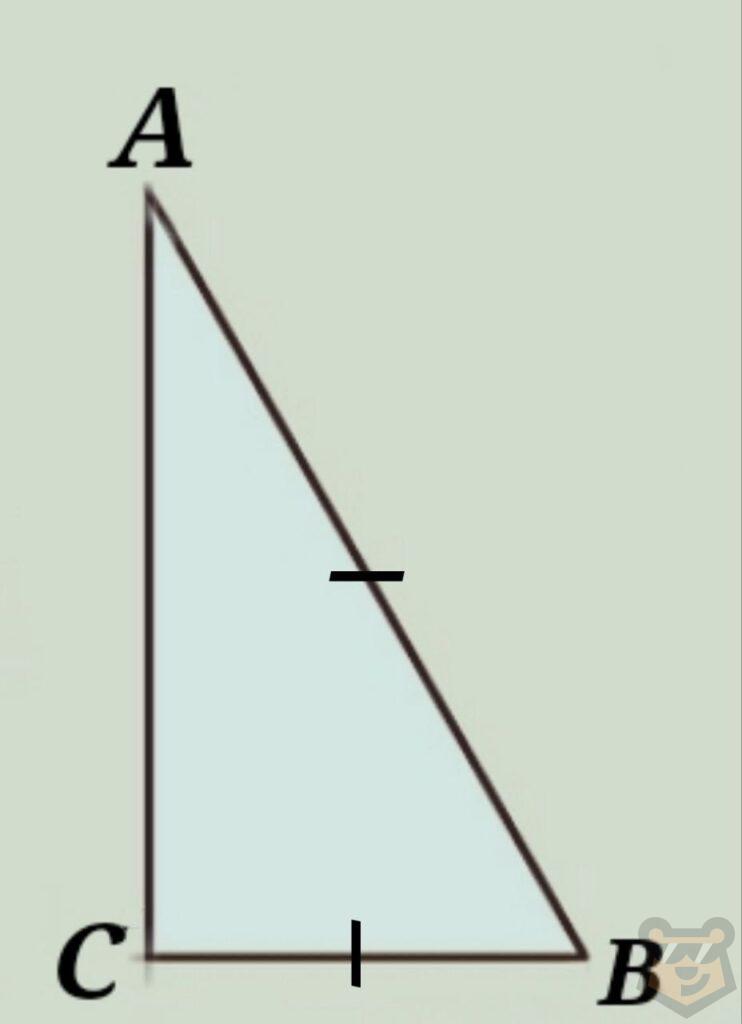
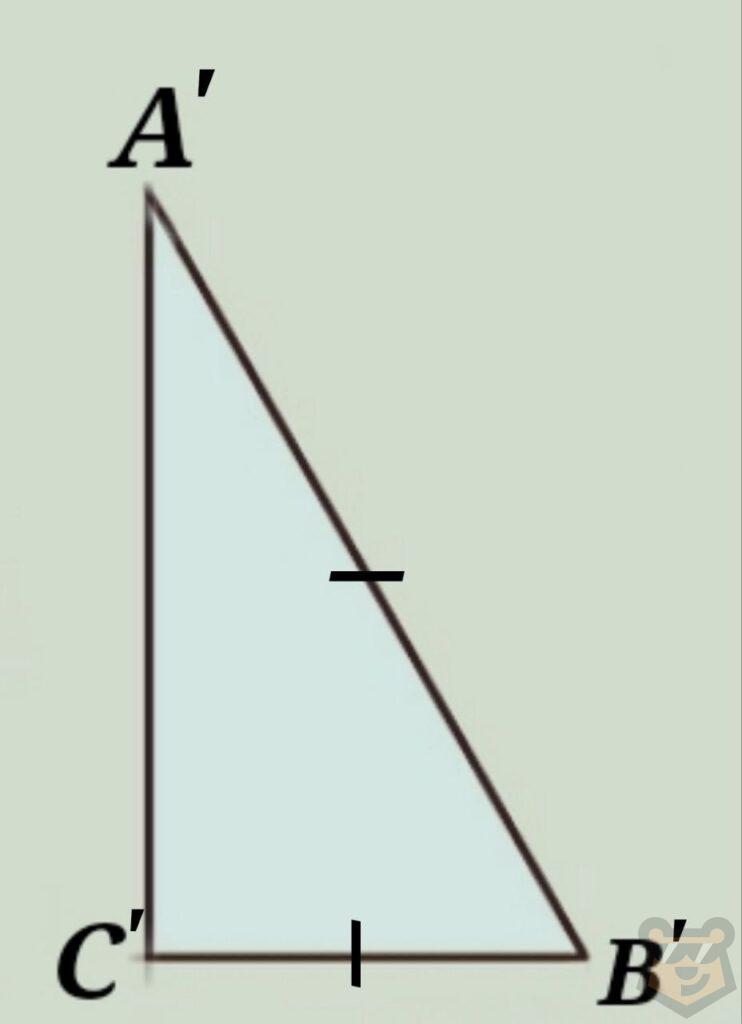
3) Два прямоугольных треугольника равны если катет и прилежащий к нему острый угол одного из них равен катету и прилежащему к нему острому углу второго.
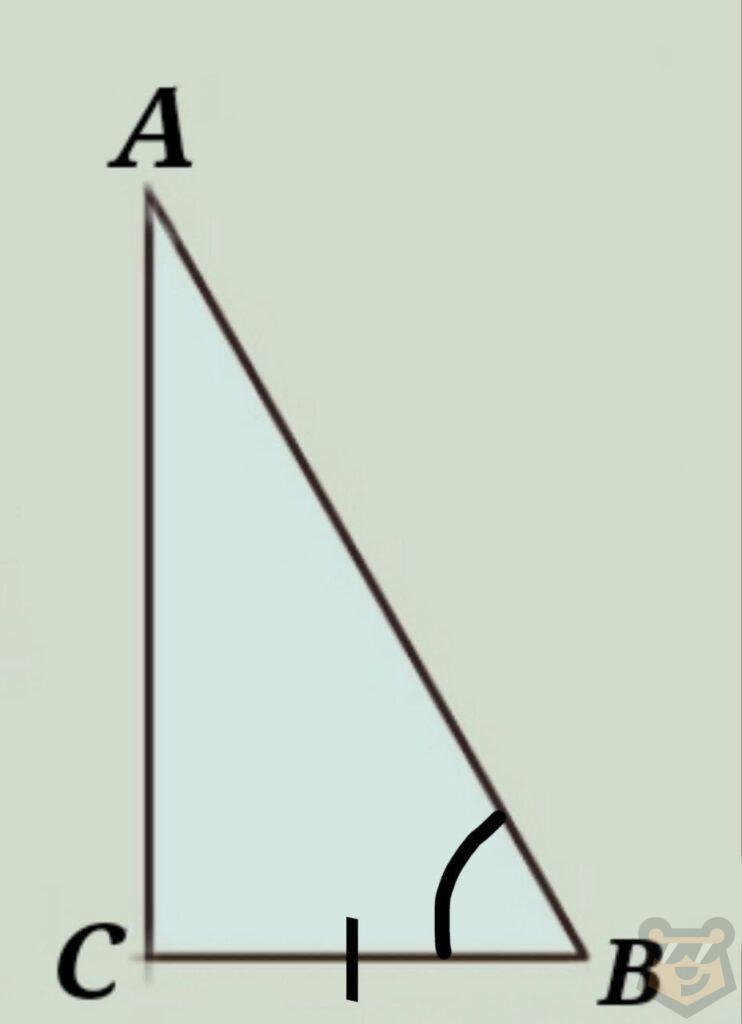
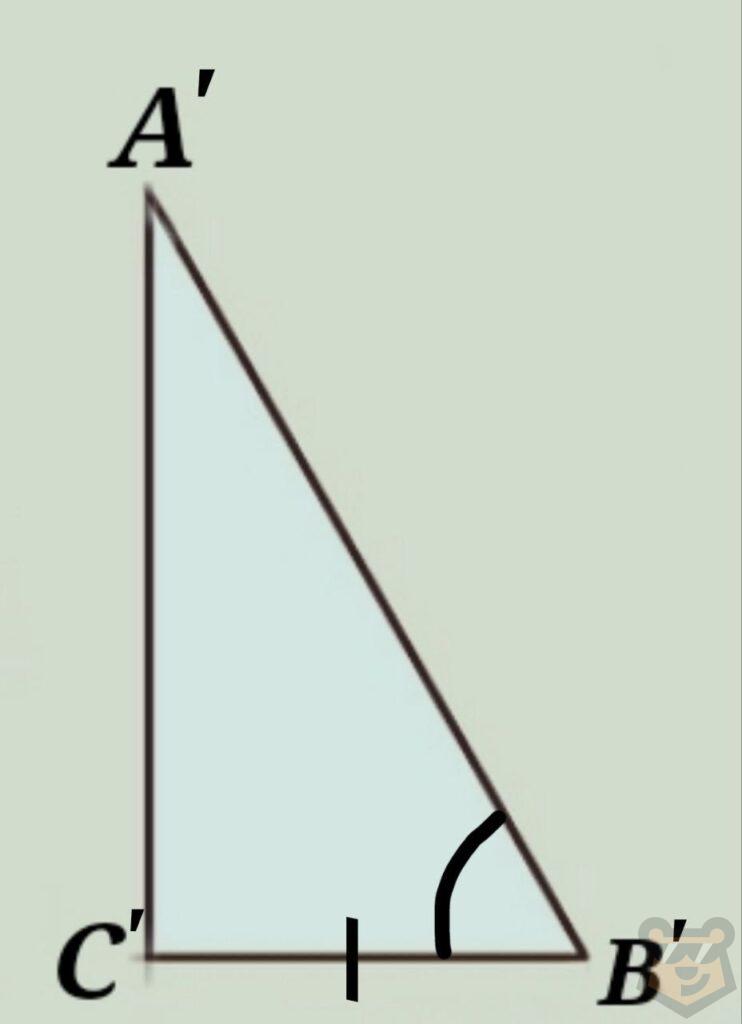
4) Два прямоугольных треугольников равны если гипотенуза и острый угол одного из них равен гипотенузе и острому углу второго.
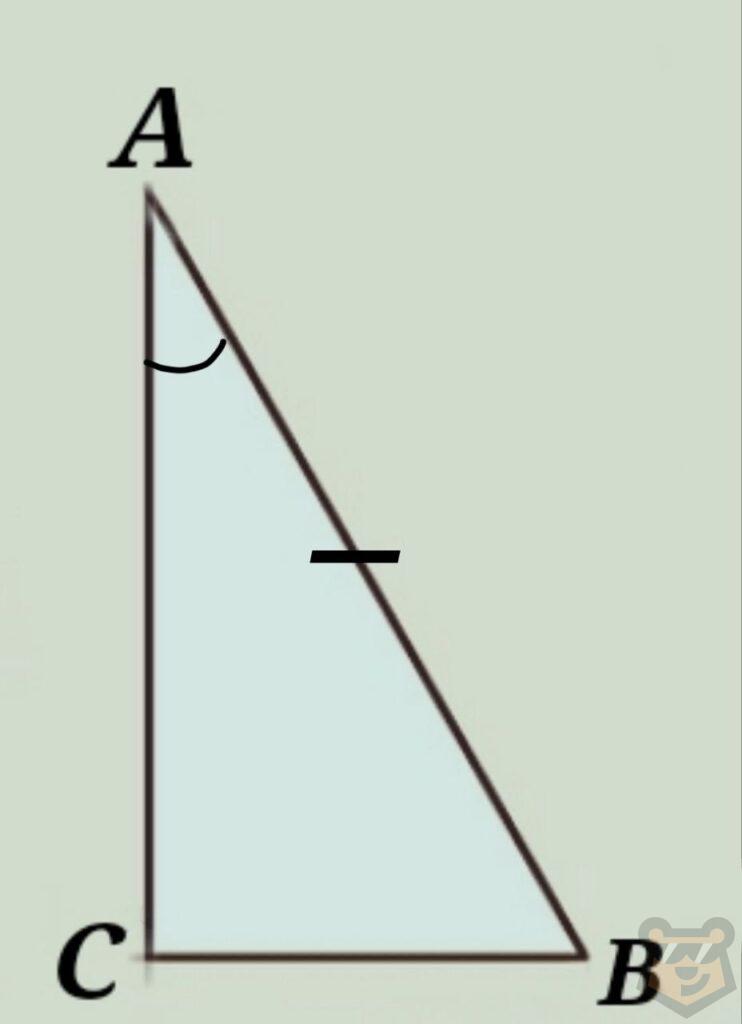
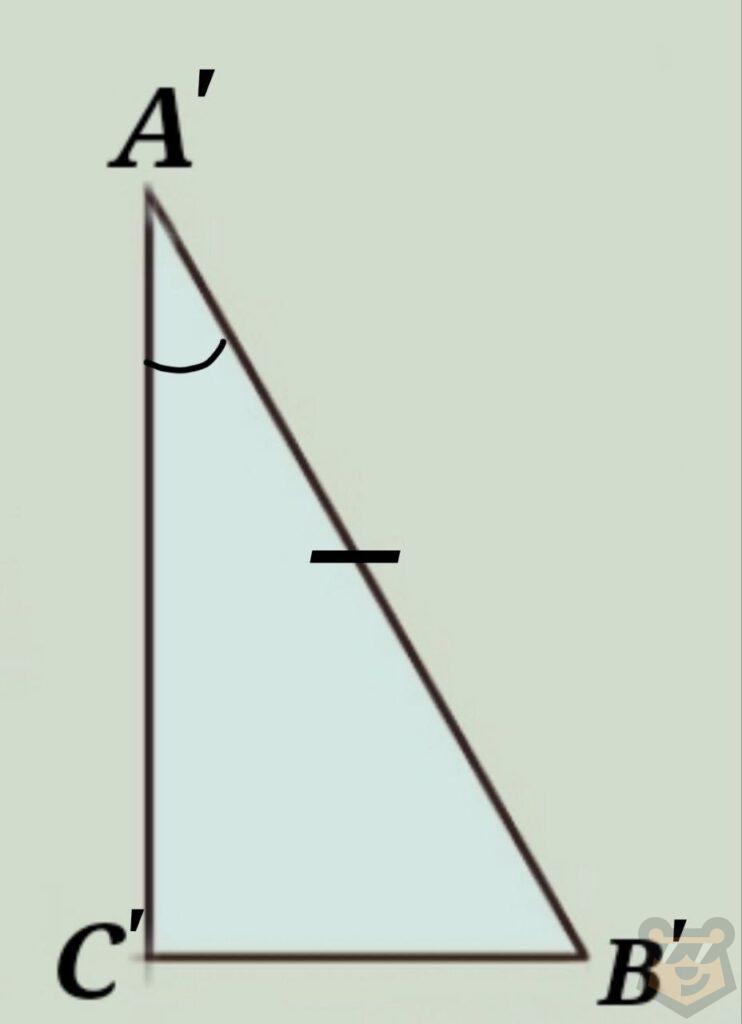
Подобные треугольники.
Подобные фигуры это такие фигуры, у которых несмотря на различия в размерах, одинаковая форма.
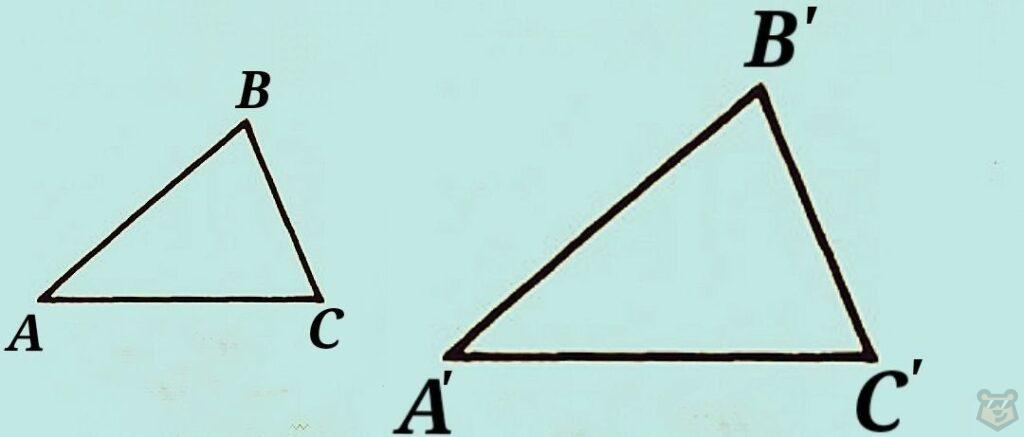
В целом подобные треугольники это те треугольники, у которых углы равны, а стороны имеют разные длины. Но стоит понимать, что у каждой пары сторон один и тот же коэффициент подобия. То есть если большая сторона первого треугольника в три раза больше большей стороны во втором треугольнике, то подобное соотношение работает и с оставшимися сторонами.
Для того чтобы два треугольника были подобны нужно соблюдение одного из трех нижеперечисленных условий.
I условие. Два угла одного треугольника соответственно равны двум углам другого треугольника.
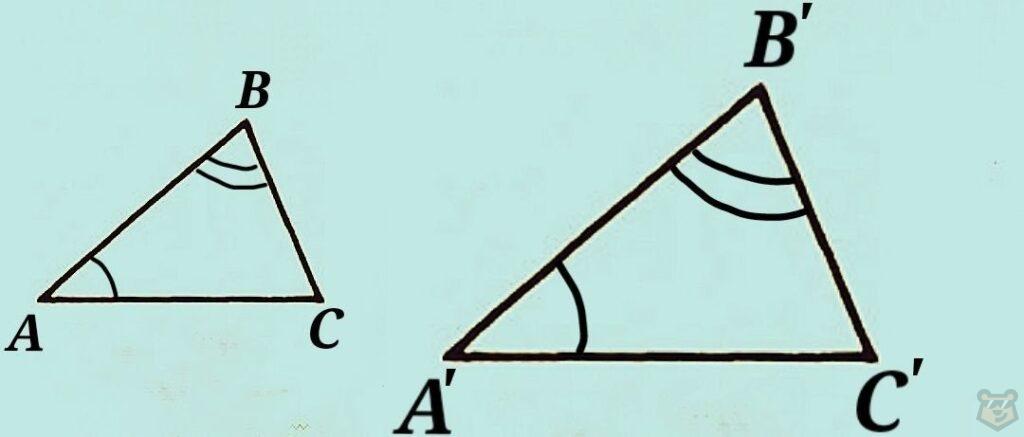
∆АВС ~ ∆А’В’С’, если ∠А = ∠А’, ∠В = ∠В’
II условие. Угол одного треугольника равен углу второго треугольника и стороны, образовавшие эти углы пропорциональны.
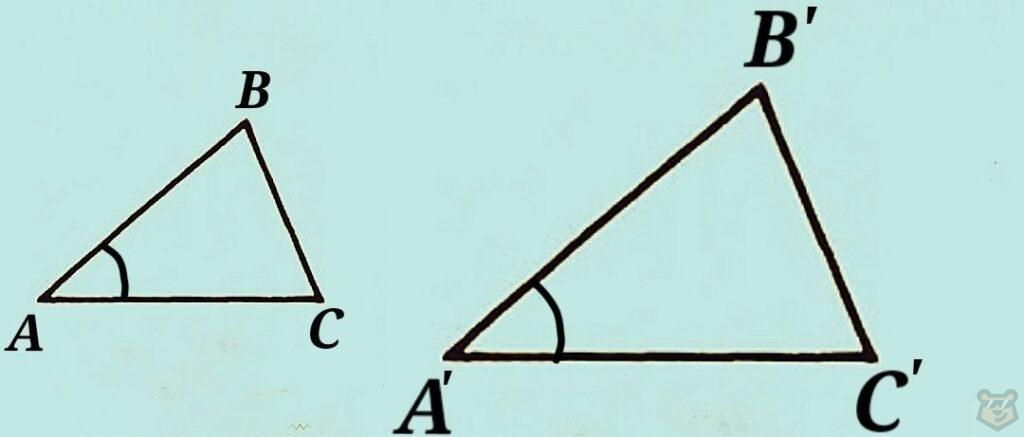
∆АВС ~ ∆А’В’С’, если ∠А = ∠А’ и А’В’/АВ = А’С’/АС
III условие. Три стороны в одном треугольники пропорциональны трем сторонам в другом треугольнике.
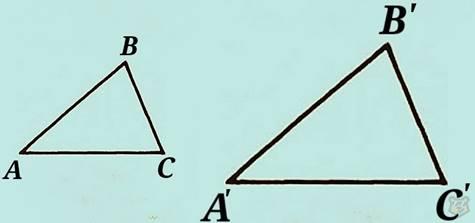
∆АВС ~ ∆А’В’С’, если А’В’/АВ = А’С’/АС = В’С’/ВС
Высота, медиана, биссектриса, средняя линия треугольника.
Высота — это отрезок, соединяющий одну из вершин треугольника с противолежащей ей стороной под углом 90 градусов.
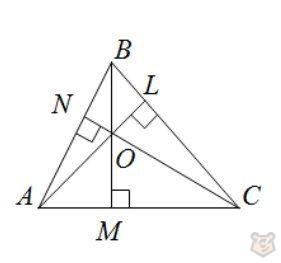
Высоту, как и все отрезки, называют двумя заглавными буквами. Обычно называют буквой вершины треугольника и буквой Н.
Например, АН, ВН, СН и так далее.
Запомни!
Любая высота в равностороннем треугольнике и высота, проведенная к основанию равнобедренного треугольника, являются также и медианой, и биссектрисой.
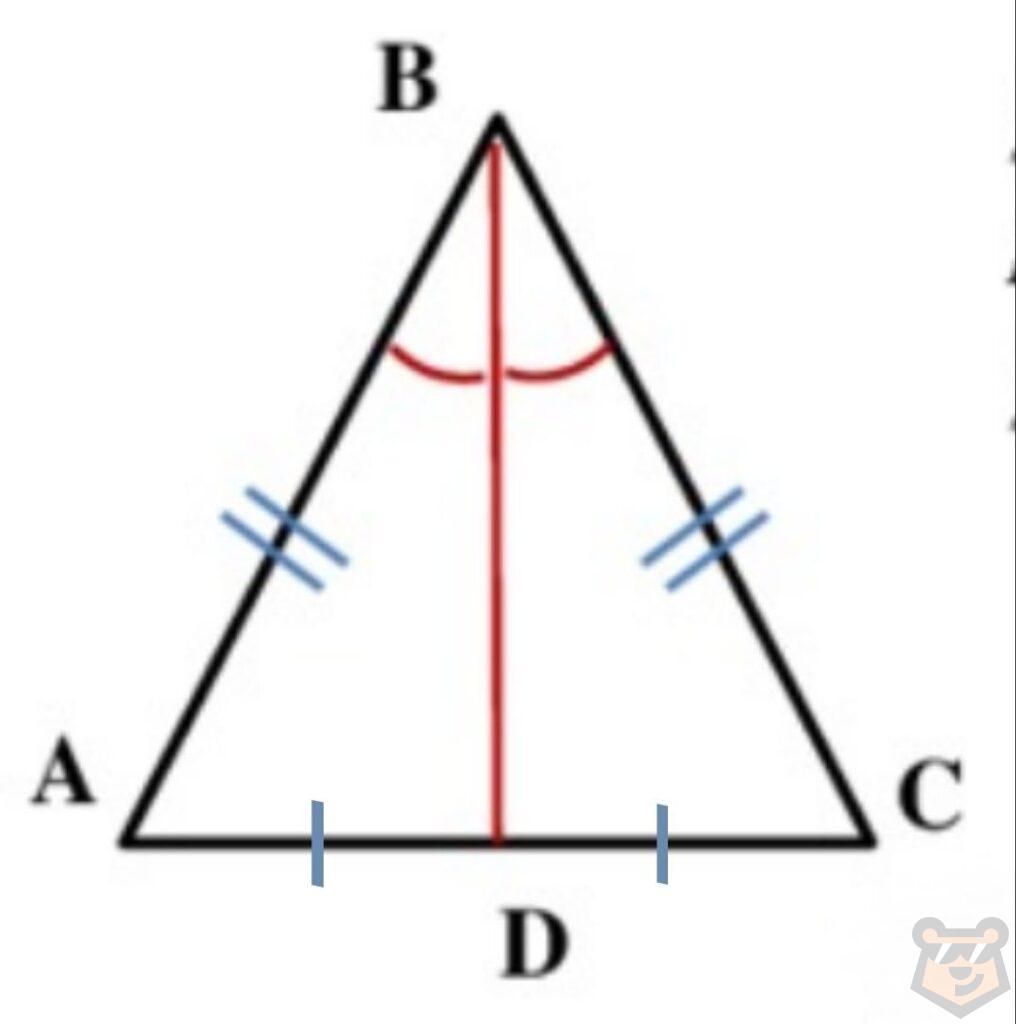
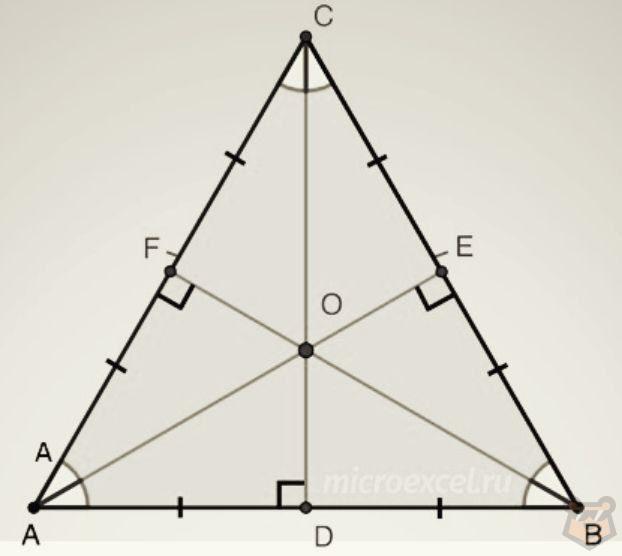
Заруби себе это на носу. Потому что данную особенность важно знать, для того чтобы облегчить решение некоторых задач.
Медиана — это такой отрезок, который соединяет одну из вершин треугольника с серединой стороны, противолежащей ей.
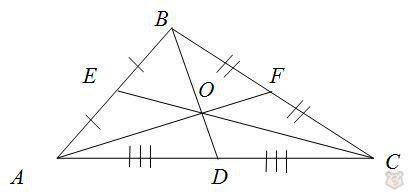
Медиану также принято называть заглавными буквами. Допустим, ВF, CD и тому подобное.
AE = EB
BF = FC
CD = DA
У медиан есть необычное свойство. Три медианы в точке пересечения делятся на два отрезка, которые относятся как 1:2.
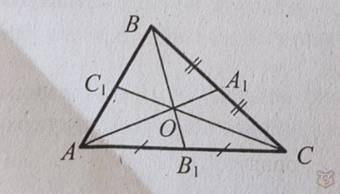
А1О : АО как 1:2
АО : АА1 как 2:3
А1О : АА1 как 1:3
Биссектриса — это отрезок, который соединяя одну из вершин треугольника с противолежащей стороной, делит угол при вершине на две равные части.
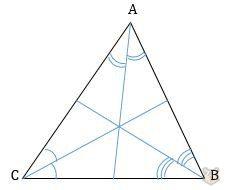
Ее также обозначают различными заглавными буквами.
У биссектрисы тоже есть особое свойство. Она делит третью часть на два отрезка, которые относятся к другу к другу как две другие стороны.
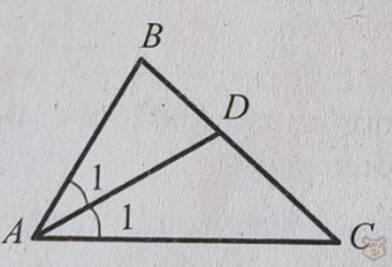
ВD / DC = AB / AC
Определение можно легко запомнить благодаря всем известной шуточной форме.
Биссектриса — это крыса, которая бегает по углам и делит угол пополам.
| Биссектриса в геометрии: | Биссектриса по факту: |
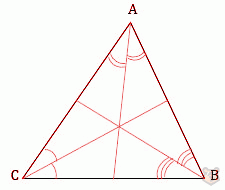 |  |
Средняя линия треугольника — это отрезок, который соединяет середины двух сторон.
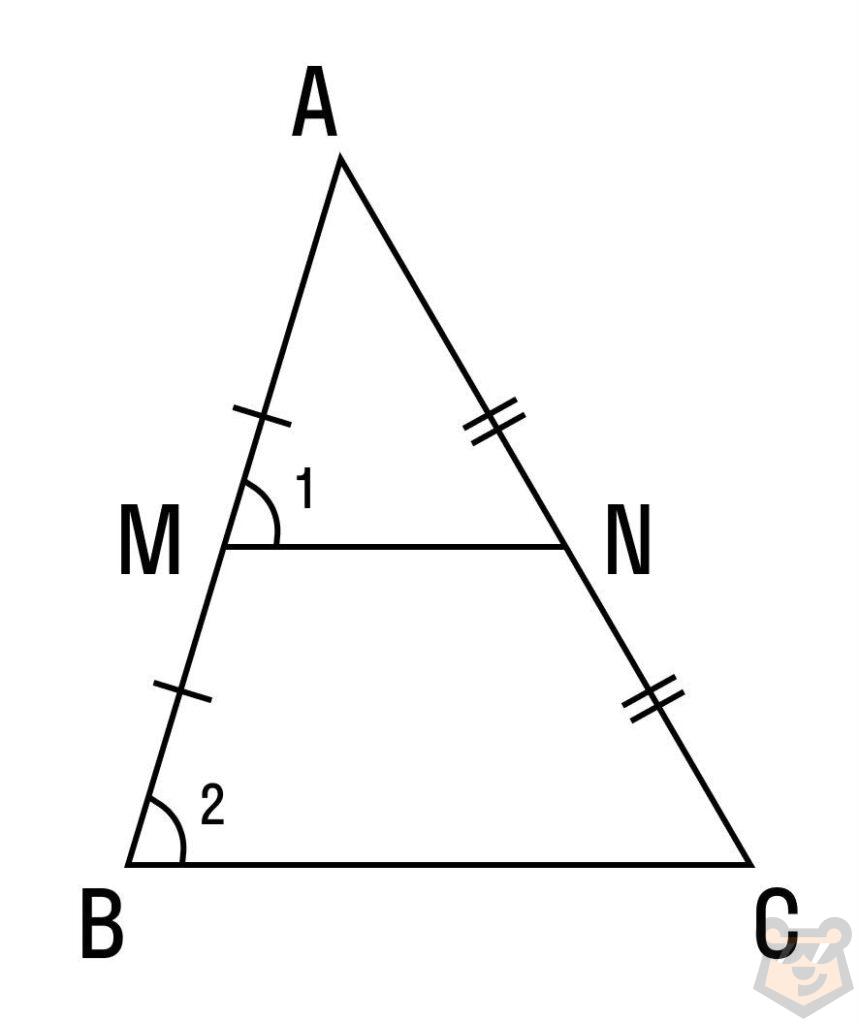
AМ = МB
АN = NC
Средняя линия параллельна третьей стороне треугольника, а также равна половине этой стороны.
МN ll BC
МN = BC / 2
Средняя линия «отрезает» подобный треугольник, площадь которого является одной четвертой площади оригинального треугольника.
∆АВС ~ ∆АМN
S∆АВС = 4 × S∆АМN
Теорема Пифагора.
Среди математиков есть такое мнение, что ничего страшного нет в том, что человек не знает формулу Герона или теорему синусов, но если человек не знаком с легендой под названием «Теорема Пифагора», то принимать его в свои математические круги не стоит. Потому что данная теорема является основой, можно даже смело сказать, фундаментом многих задач по геометрии, которые встречаются не только на уроках в школе, но и на итоговой аттестации, и тем более на ЕНТ.

Теорема Пифагора — это теорема, предназначенная для прямоугольных треугольников. Звучит она следующим образом:
Сумма квадратов катетов равна квадрату гипотенузы.
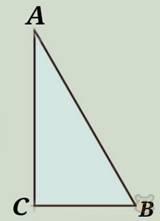
Вернемся к знакомому чертежу. Но теперь давайте каждую сторону назовем строчной буквой, которая соответствует углу, лежащему напротив.
То есть АВ — это с, ВС — а, АС — b.
В таком случае, а и b — это наши катеты, а с — это наша гипотенуза.
И тогда сделаем запись нашей теоремы математическим языком: c^2 = a^2 + b^2
Выходит, что благодаря этой формуле мы зная две стороны прямоугольного треугольника можем с легкостью найти длину третьей.
Раньше в учебниках теорему Пифагора доказывали и объясняли на примере площадей трех квадратов, сторонами которых были три отрезка, обещающих прямоугольный треугольник. И в связи с этим ученики запоминали формулу благодаря шуточной терминологии: «Пифагоровы штаны во все стороны равны».
Теорема косинусов.
Можно сказать, что это теорема является усовершенствованной теоремой Пифагора. Потому что она строится примерно по такому же принципу, но уже подходит для всех треугольников.
Теорема: Квадрат одной стороны равен сумме квадратов двух других сторон, от которой отняли удвоенного произведение этих сторон друг на друга и на косинус угла между ними.
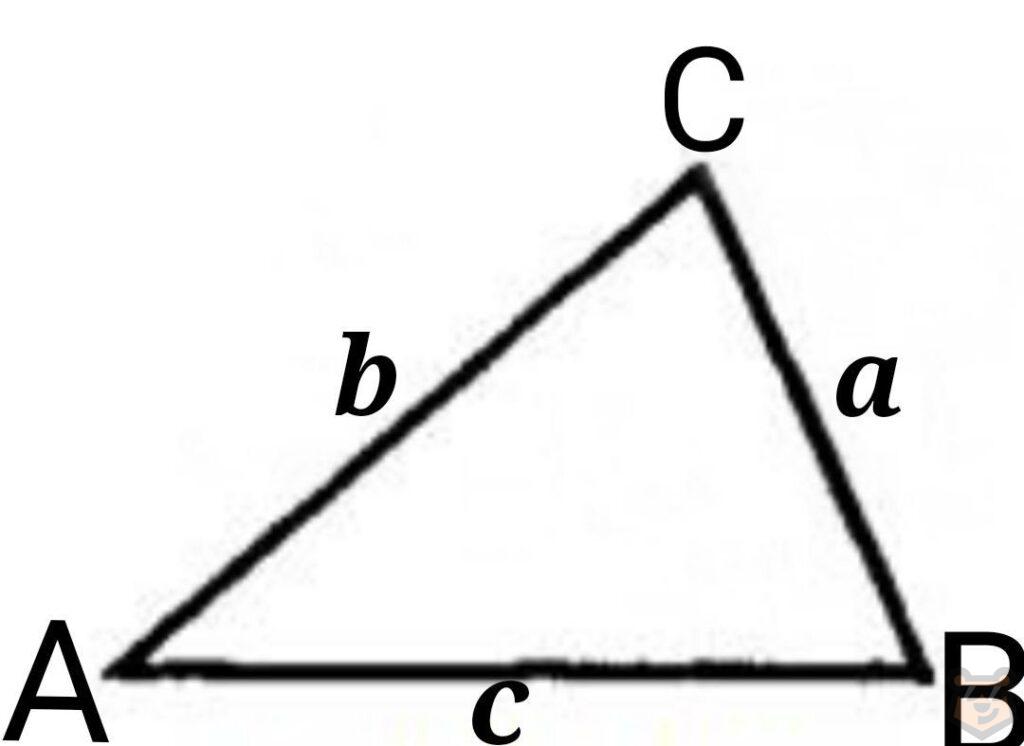
Используя предоставленный чертеж и определение теоремы составим формулы.
а^2 = b^2 + c^2 — 2×a×b×cosA
b^2 = a^2 + c^2 — 2×a×b×cosB
c^2 = a^2 + b^2 — 2×a×b×cosC
Теорема синусов
Данная теорема демонстрирует нам взаимосвязь сторон и синусов углов. Она тоже подходит для произвольных треугольников.
Теорема синусов гласит: отношение синуса каждого угла к противолежащей ему стороне одинакова.
Возьмем еще один чертеж. И с помощью него лучше поймем нашу теорему и сделаем для нее математическую запись.
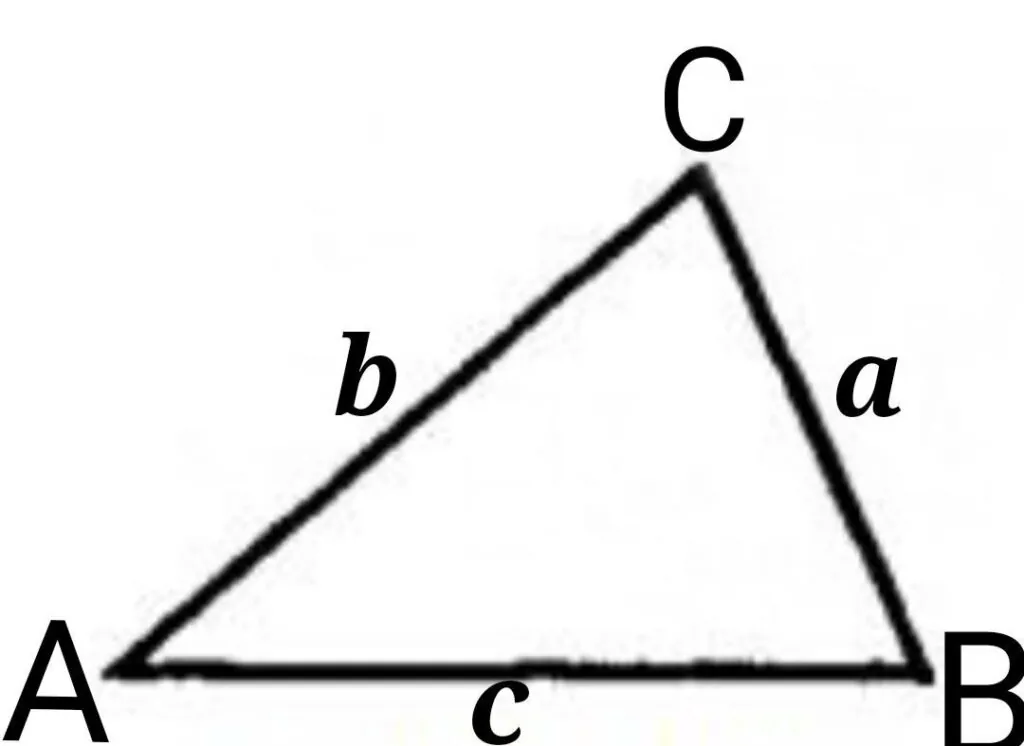
a / sinA = b / sinB = c / sinC
Площади треугольников.
Формула для вычисления площади треугольника зависит от его вида. Для каждого типа есть свой способ.
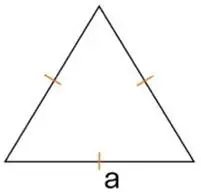
Площадь равностороннего треугольника.
Площадь равностороннего треугольника находится по формуле: S = a^2 × √3 / 4
Площадь прямоугольного треугольника.
Если взять два одинаковых прямоугольных треугольника, то можно будет сложить их в прямоугольник. В таком случае площадь двух треугольников будет равна половине площади четырехугольника.
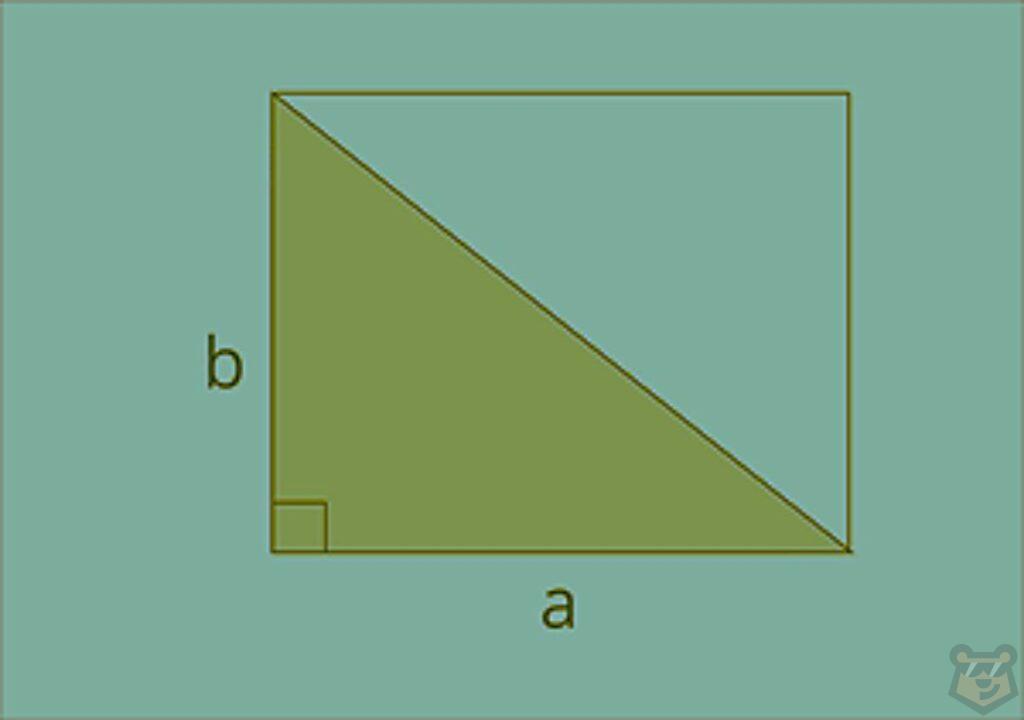
Площадь прямоугольника находится по формуле S = a×b. Тогда площадь одного прямоугольного треугольника будем вычислять с помощью выражения: S = a×b/2.
а и b — это наши катеты.
Площадь равнобедренного треугольника.
Если в равнобедренном треугольнике провести высоту к его основанию, то мы разделим его на два равных прямоугольных треугольника. Из двух новых полученных фигур можно будет сложить прямоугольник, площадь которого будем искать используя ту же формулу S = a×b.
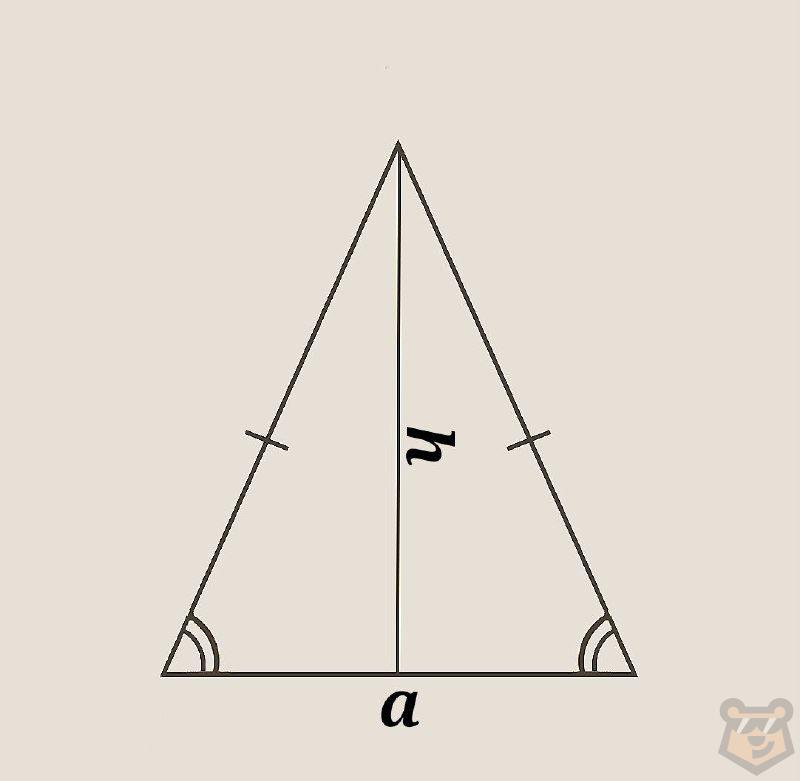
Только в данном случае мы получим S = a/2×h. Потому что длиной прямоугольника будет наша высота h, а шириной будет сторона а, деленная на 2. Потому что как мы видим у двух треугольников катетом является не вся сторона, а только ее половина. Половина так как высота в равнобедренном треугольнике, проведенная к основанию, одновременно является медианой.
Тогда площадь равнобедренного треугольника надо искать по формуле S = a×h/2.
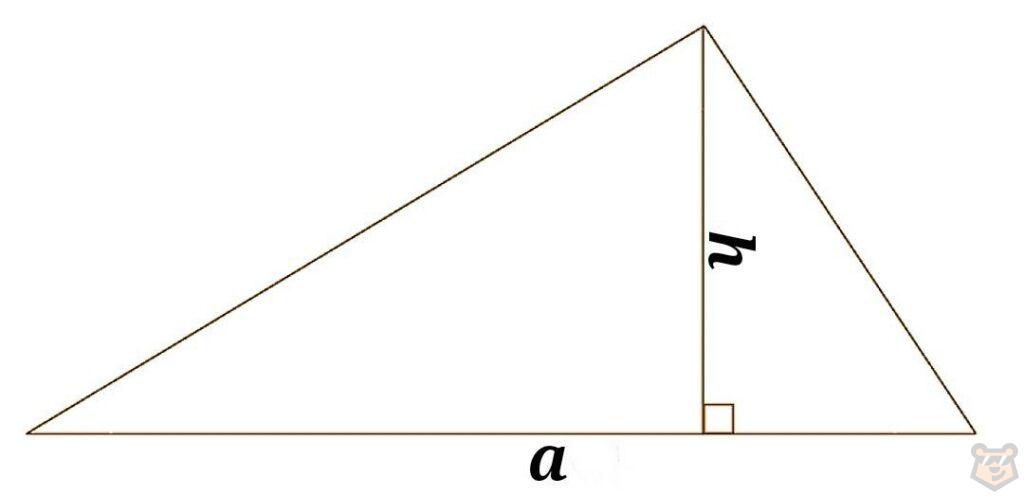
Площадь других треугольников.
Площадь произвольного треугольника равна произведению высоты на сторону, к которой та была проведена. S = a×h/2.
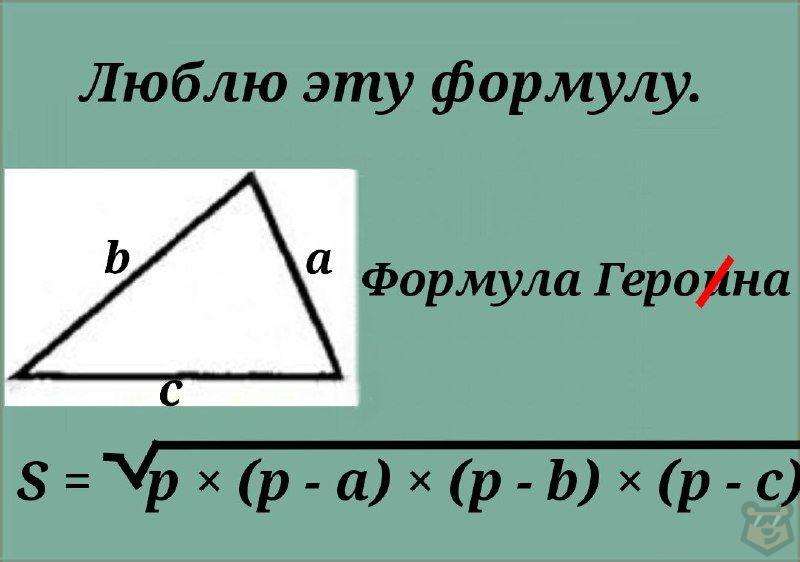
Формула Герона.
Также для вычисления формулы нередко пользуются формулой Герона. Эта формула подходит нам для вычисления площади треугольника в том случае, когда мы знаем только все три стороны. Формула имеет следующий вид:
S = √(p × (p — a) × (p — b) × (p — c))
Здесь а, b и с — это длины сторон, а р — это полупериметр.
Полупериметр находим, основываясь на таком выражении: р = Р/2 = а + b + с / 2.
Заключительные таблицы.
Для наглядности и простоты понимания составим таблицы, в которых обобщим все изученное.
Виды треугольников.
| В зависимости от углов | Остроугольный | Тупоугольный | Прямоугольный |
| Описание | три острых угла | один тупой угол | один прямой угол |
Рисунок | 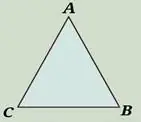 | 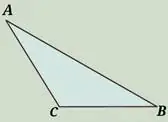 |  |
| В зависимости от сторон | Разносторонний | Равнобедренные | Равносторонний |
| Описание | три разные стороны | две равные стороны | три равные стороны |
Рисунок |
Признаки равенства треугольников.
I признак | 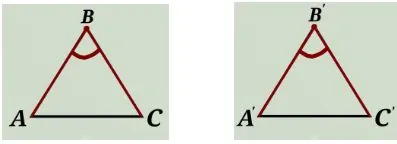 | 2 стороны1 угол |
II признак | 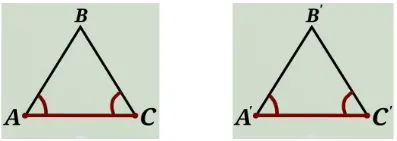 | 2 угла1 сторона |
III признак | 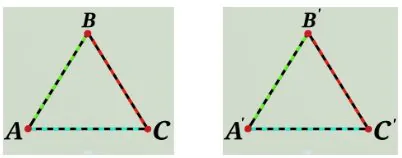 | 3 стороны |
Признаки подобия треугольника.
I признак | 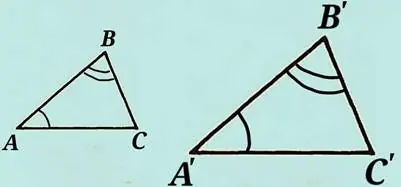 | 2 угла |
II признак | 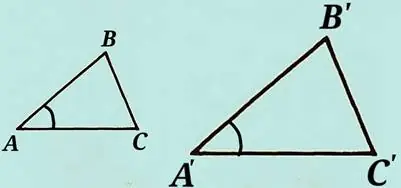 | 1 угол2 пропорциональные стороны |
III признак |  | 3 пропорциональные стороны |
Теоремы.
Теорема Пифагора. | |
Теорема косинусов. | |
Теорема синусов. |
Площадь треугольников.
 | |
 | |
 | |
 |
Практическая часть.
Задание №1. Равны ли треугольники, изображенные на рисунке ?
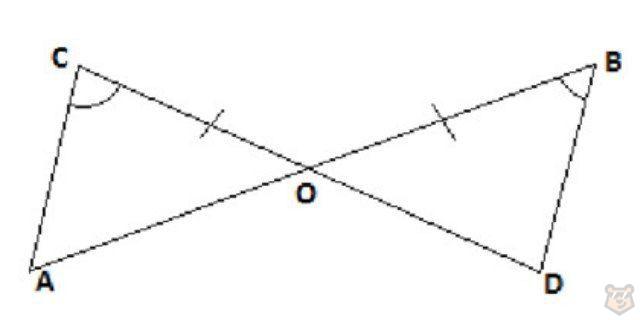
Решение. Согласно рисунку отрезки СО и ОВ равны. Это отмечено на самом чертеже. Также благодаря рисунку мы видим, что углы ОВD и ОСА равны.
Если внимательно присмотреться, то можно понять, что углы СОА и ВОD тоже равны. Потому что данные два угла являются вертикальными.
Таким образом, СО = ОВ, ∠ОВD = ∠ОСА, ∠СОА = ∠ВОD.
Выходит, что сторона и два прилежащих к ней угла одного треугольника равны стороне и двум углам другого. А это значит, что треугольники равны. ∆СОА = ∆ВОD
Ответ: Да, треугольники равны по второму признаку.
Здание №2. Подобны ли треугольники, представленные на чертеже?
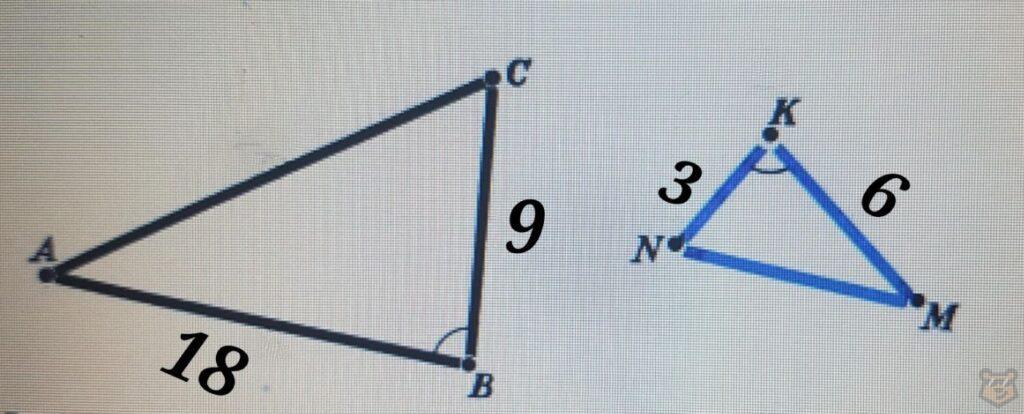
Решение. На рисунке отмечено, что угол К равен углу В. Кроме этого на чертеже указаны длины сторон. Давайте все это оформим.
∠K = ∠В
КN = 3
KM = 6
ВА = 18
BС = 9
Можно заметить, что стороны двух треугольников попарно пропорциональны.
ВА / КМ = ВС / КN
18 / 6 = 9 / 3 = 3
Выходит, что у двух треугольников два равных угла и две пары пропорциональных сторон. А это значит, что треугольники подобны.
∆АВС ~ ∆NKM
Ответ: да, подобны.
Здание №3. Вычислите периметр прямоугольного треугольника у которого гипотенуза равна 17, а один из катетов равен 8.
Решение. Р = а + b + c.
Нам известно лишь две стороны. Для того чтобы найти третью сторону, мы будем использовать теорему Пифагора, ведь наш треугольник прямоугольный.
с^2 = а^2 + b^2
Выразим из нашей теоремы недостающую сторону.
а^2 = с^2 — b^2
А сейчас просто вычислим длину нашего катета.
а^2 = 17^2 — 8^2 = 289 — 64 = 225
а^2 = 225
а = √225
а = 15
Мы нашли третью сторону теперь с легкостью можем вычислить наш периметр.
Р = 15 + 8 + 17 = 40
Ответ: 40.
Задания по данному разделу, которые встречаются на ЕНТ.
Задания на тему «Треугольник» на едином национальном тестировании присутствуют и в математической грамотности, и в профильной математике. В целом типы встречающихся задач нельзя назвать сильно сложными. Но все же давайте посмотрим как правильно их решать.
Математическая грамотность
Задание №1. Лестница длиной 12,5 метров приставлена к стене таким образом, что верхний конец лестницы находится от земли на высоте 12 метром. Найдите расстояние от нижнего конца лестницы до стены.
Решение. Если начертить чертеж, то получим следующее:
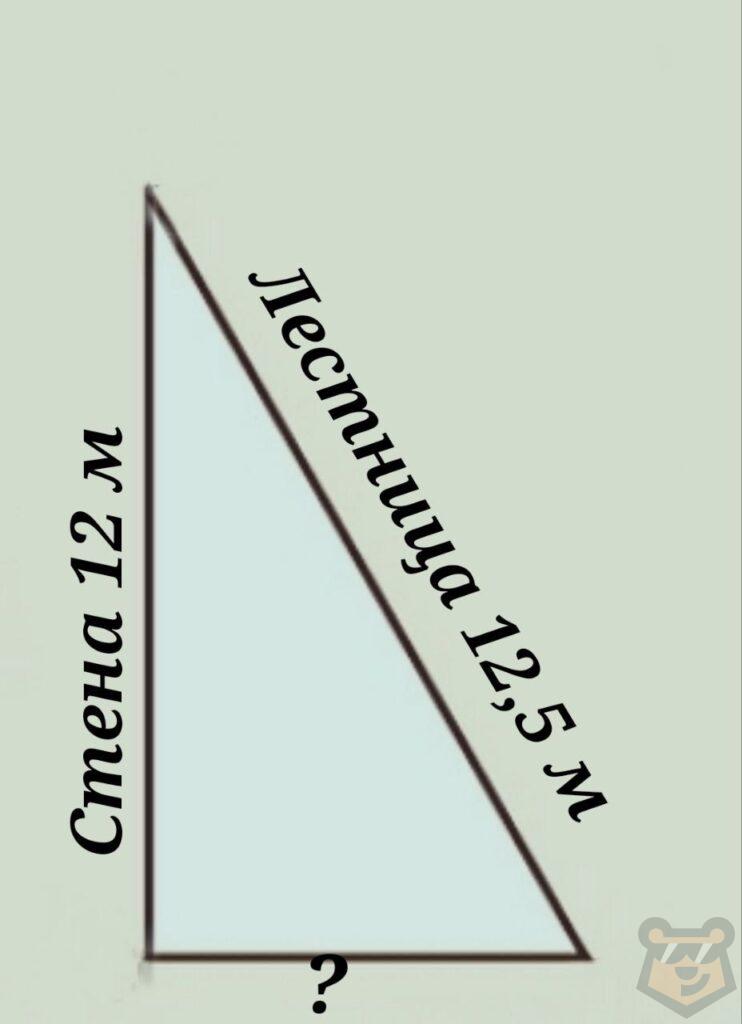
Это будет прямоугольный треугольник. Для решения этой задачи используем теорему Пифагора.
с^2 = а^2 + b^2
Выразим отсюда катет и решим.
а^2 = с^2 — b^2
а^2 = 12,5^2 — 12^2 = 156,25 — 144 = 12,25
а^2 = 12,25
а = √12,25
а = 3,5
Ответ: 3,5
Задание №2. Ниже представлен квадрат. Площадь его закрашенной части равна 18. Найдите чему равен периметр квадрата.
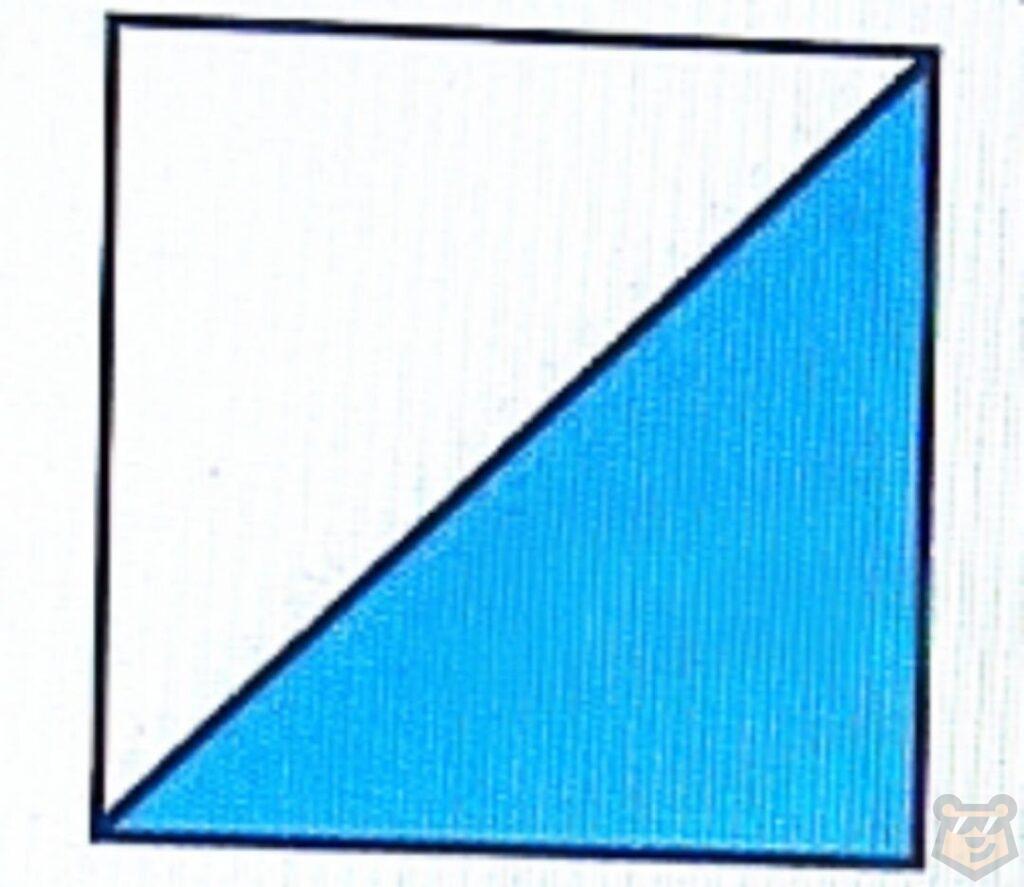
Решение. Для того того чтобы найти периметр квадрата, нам необходимо вначале найти чему равны его стороны.
До этого мы упоминали, что диагональ в прямоугольник делит его на два равных треугольника. С квадратом происходит то же самое. То есть площадь квадрата равна площадь запущенной части, умноженная на два.
S = 2 × S∆ = 2 × 18 = 36
Вспомним, что площадь квадрата находится по формуле S = a^2.
а^2 = 36
а = √36
а = 6
Вот теперь найдем периметр квадрата с помощью формулы Р = 4а
Р = 4 × 6 = 24
Ответ: 24.
Задание №3. Периметр треугольника равен 85. Отношение длины первой стороны к другой равно 1:2. Отношение длины второй стороны к третьей равно 3:4. Чему равно произведение этих 3 сторон.
Решение. Наименьшую сторону, то есть первую, представим как х.
Тогда согласно пропорции, вторая сторона будет равна 2х.
Теперь найдем 3 сторону, соблюдая наше соотношение.
2х : у
3 : 4
у = 2х × 4 / 3 = 8х/3
В итоге получим:
| 1 сторона | х |
| 2 сторона | 2х |
| 3 сторона | 8х / 3 |
Вспомним, что периметр это сумма всех сторон. Значит, получим следующее выражение: х + 2х + 8х / 3 = 85
Решим данное уравнение и найдем длины наших сторон.
3х + 8х / 3 = 85
3х × 3 +8х / 3 = 85
9х+8х / 3 = 85
17х /3 = 85
17х = 85 × 3
17х = 255
х = 255/17
х = 15
Возвращаемся к нашей таблице
| 1 сторона | х | 15 | |
| 2 сторона | 2х | 2×15 | 30 |
| 3 сторона | 8х / 3 | 8×15/3 | 40 |
Теперь найдем произведение данных трех значений.
15 × 30 × 40 = 18 000
Ответ: 18 000.
Математика.
Задание№1. Расстояние между центром шара и плоскостью сечения равно 8. Радиус шара 10. Тогда радиус сечения равен.
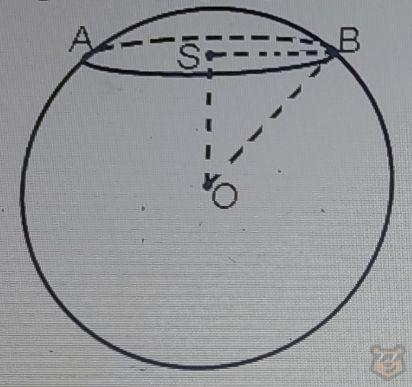
Решение. По чертежу видно, что радиус сечения это ничто иное, как катет прямоугольного треугольника. Мы знаем две стороны, значит можем легко найти третью с помощью теоремы Пифагора.
с^2 = а^2 + b^2
Выразим отсюда катет и решим.
а^2 = с^2 — b^2
а^2 = 10^2 — 8^2 = 100 — 64 = 36
а^2 = 36
а = √36
а = 6
Ответ: 6.
Задание №2. Дан треугольник, у которого стороны равны 4, 5 и 6. Найдите проекцию средней стороны на большую.
Решение. Что такое проекция? Для того чтобы это понять обратимся к чертежу.
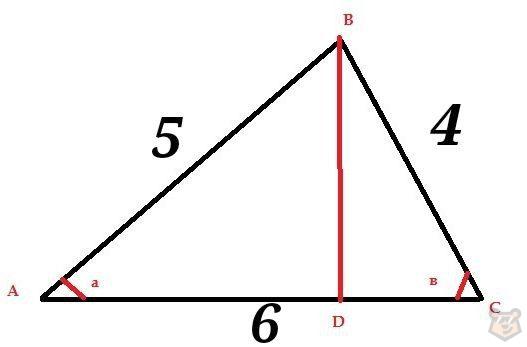
Мы провели высоту ВD. Отрезок разделили сторону АС на две части АD и DC.
Проекцией стороны ВС на АС будет отрезок DC.
А проекцией стороны АВ на АС будет отрезок АD.
Для того чтобы вычислить нужную проекцию есть несколько способов. Но выберем самый простой.
Смотря на наш чертеж мы видим, что высота разделили первоначальный треугольник на два прямоугольных треугольника. У них есть общая сторона ВD.
ВD можно будет вычислить через теорему Пифагора используя любой из треугольников.
с^2 = а^2 + b^2
а^2 = с^2 — b^2
ВD^2 = АС^2 — DC^2
ВD^2 = АB^2 — AD^2
Мы не знаем чему равны отрезки АD и DC. Но нам известно, что они оба составляют отрезок АС, равный 6. Это значит, что они в сумме дают шесть.
АD + DC = 6
Получается, что благодаря этому выраженную мы получим следующие:
АD = 6 — DC
DC = 6 — AD
Поскольку мы ищем проекцию средней стороны (АВ) на большую сторону АС, то будем делать упор на отрезок АD, который и является нашей проекцией.
Давайте представим АD как х.
Тогда DC = 6 — х ( потому что DC = 6 — AD).
Теперь подставим все наши числовые значения в данные две записи:
ВD^2 = ВС^2 — DC^2
ВD^2 = АB^2 — AD^2
ВD^2 = 4^2 — (6 — х)^2
ВD^2 = 5^2 — х^2
Для того чтобы найти чему равен наш х (то есть отрезок АD) мы приравняем данные два выражения.
4^2 — (6 — х)^2 = 5^2 — х^2
16 — (6 — х)^2 = 25 — х^2
Раскроем скобку (6 — х)^2 с помощью формулы сокращённого умножения.
(а — b)^2 = a^2 — 2ab + b^2
(6 — х)^2 = 6^2 — 2×6×x + x^2 = 36 — 12x + x^2
Подставляем, но пока только в скобках. Ведь перед первоначальным выражением стоит знак минус. А если это так, то необходимо не забыть поменять знаки на противоположные.
16 — (36 — 12x + x^2) = 25 — х^2
16 — (36 — 12x + x^2) = 25 — х^2
16 — 36 +12х — х^2 = 25 — х^2
-20 +12х -х^2 = 25 -х^2
Переносим значения с переменной х в одну сторону, а числовые значения в другую. Не забудьте поменять знаки на противоположные.
12х — х^2 + х^2 = 25 + 20
12х = 45
х = 45/12
х = 3,75
Ответ: 3,75.
Задание№3. Плоскость пересекает сферу, у которой радиус равен 29. Расстояние между центром сферы и данной плоскостью равно 20. Найдите радиус, образовавшегося сечения.
Решение. Похожее задание мы уже решали. Вновь обращаемся к теореме Пифагора.
с^2 = а^2 + b^2
Выразим отсюда катет и решим. а^2 = с^2 — b^2
а^2 = 29^2 — 20^2 = 841 — 400 = 441
а^2 = 441
а = √441
а = 21
Ответ: 21.
Задание №4. Прямая CD и сторона АВ параллельны. Угол DCB равен 50°, а градусная мера угла АСВ равен 60. Найдите чему равны другие два внутренних угла треугольника.
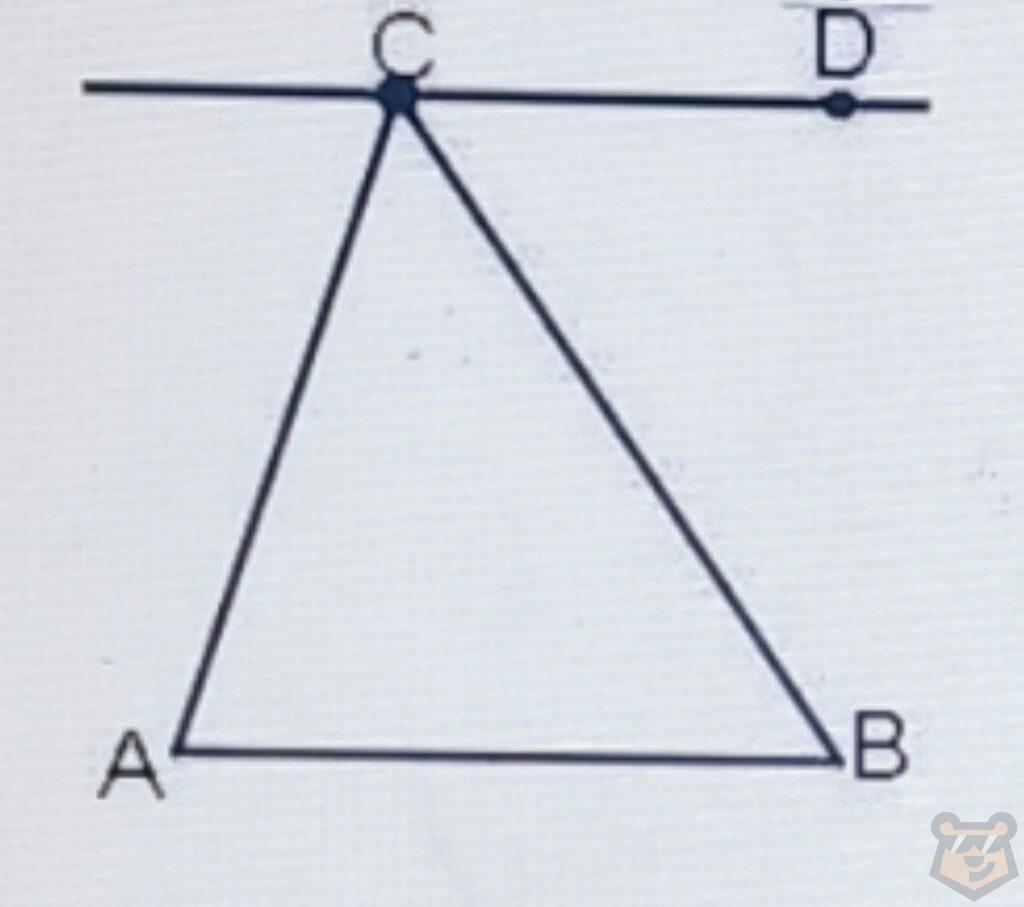
Решение. Запишем все что нам известно.
СD ll AB
∠DCB = 50°
∠ACВ = 60°
∠ABC и ∠САВ — ?
Обратим внимание на два угла. Это ∠DCB и ∠ABC. Если вспомнить, что сторона АВ и прямая, которой принадлежит отрезок CD, параллельны, то можно легко понять что эти два угла являются внутренними накрест лежащими. А это значит, что их градусные меры равны.
∠ABC = ∠DCB = 50°
Теперь вернемся к последнему углу САВ.
Вспомним, что сумма внутренних углов треугольника всегда равняется 180 градусам.
∠АВС + ∠АСВ + ∠САВ = 180°
Выразим отсюда угол САВ.
∠САВ = 180° — ∠АВС — ∠АСВ
∠САВ = 180° — 50° — 60° = 70°
Ответ: 50°, 70°.
Задание №5. Площадь правильного треугольника равна 4√3. Найдите чему равна сторона такого треугольника и чему равен его периметр.
Решение. Правильный треугольник — это треугольник, у которого все стороны равны. Для того чтобы найти площадь такой фигуры, используют формулу: S = a^2 ×√3 /4.
Сделаем следующую запись: 4√3 = a^2 ×√3 /4
Теперь вычислим сторону треугольника.
Перенесем знаменатель в ту сторону, где его нет. Получим :
4√3 × 4 = a^2 ×√3
16√3 = a^2 ×√3
Теперь избавимся от √3. Так как он есть и в правой и в левой части
16 = а^2
Можно сделать более привычную запись.
а^2 = 16
Теперь легко найдем сторону а.
а = 4
Теперь зная сторону можно легко найти периметр треугольника. С учетом того, что у нас три одинаковые стороны формула примет такой вид: Р = 3×а
Р = 3×4 = 12
Ответ: 4, 12.
Задание №6. Из некоторой точки А верхушка дерева видна под углом 45°. Если удалиться от дерева по прямой ОА еще на 10 м, то верхняя точка будет видна под углом 60°. Вычислите высоту дерева.
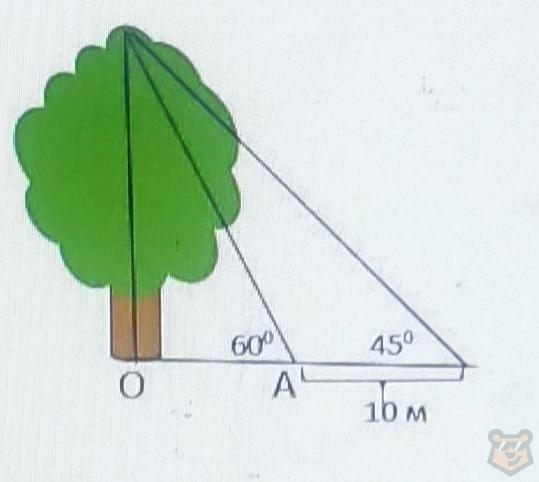
Решение. Давайте назовем углы самого большего треугольника буквами С и В.
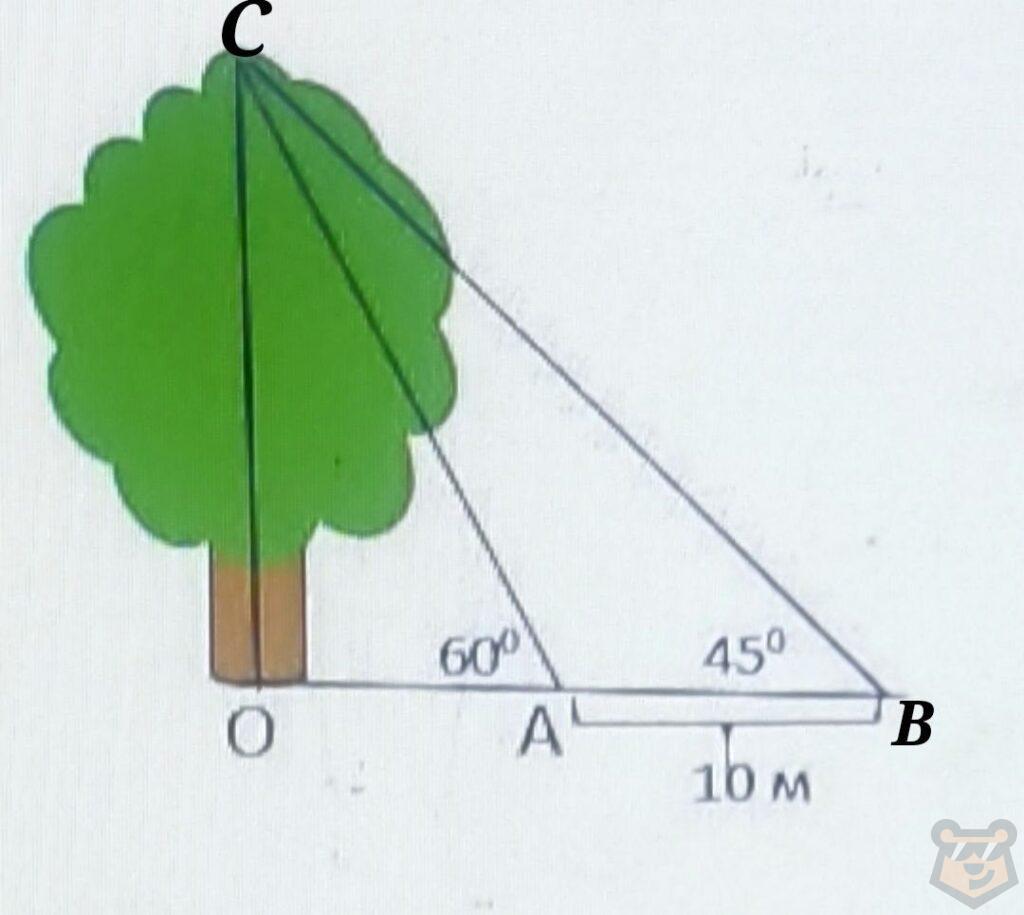
Обратим внимание на то, что угол О равен 90 градусам, а угол В равен 45 градусам. Сейчас найдем чему равен угол С.
∠С = ∠О — ∠В
∠С = 90° — 45° = 45°
Таким образом, углы С И В равны. ∠С = ∠В = 45°
А из этого вытекает то, что треугольник СОВ является равнобедренным. Значит, сторона ОВ равна стороне ОС.
Сейчас лучше присмотримся к треугольнику СОА. От тоже прямоугольный.
∠О = 90°
∠САО = 60°
Найдем чему равна градусная мера угла ОСА.
∠ОСА = ∠О — ∠САО
∠ОСА = 90° — 60° = 30°
Вспомним то, что катет, лежащий напротив угла 30 градусов, равен половине гипотенузе.
Тогда получится, что ОА = СА / 2
Выразим отсюда СА.
СА = 2 × ОА.
Пусть ОА будет х.
Тогда СА = 2х.
А сторона ОВ = 10 + х.
Учитывая то, что ОС равняется ОВ, то выйдет, что ОВ тоже равно 10 + х.
Тогда стороны в треугольнике СОА будет таковы.
ОС = 10 + х
ОА = х
СА = 2х
Давайте с помощью теоремы Пифагора, которая подходит для нашего треугольника, потому что он прямоугольный найдем х.
с^2 = а^2 + b^2
Гипотенуза (с) — СА
Катеты (а и b) — ОА и ОС
СА^2 = ОА^2 + ОС^2
Подставляем наши значения с переменной х.
(2х)^2 = х^2 + (10 + х)^2
4х^2 = х^2 + (10 + х)^2
Раскроем скобку (10+х)^2 с помощью формулы сокращённого умножения.
(а + b)^2 = a^2 + 2ab + b^2
(10+х)^2 = 100 + 20х + х^2
Подставляем
4х^2 = х^2 + 100 + 20х + х^2
4х^2 = 2х^2 + 100 + 20х
Перенесем все значения в левую сторону, меняя знаки.
4х^2 — 2х^2 — 100 — 20х = 0
2х^2 — 20х -100 = 0
Разделим обе части уравнения на 2. Выйдет следующее.
х^2 — 10х — 50 = 0
Решим уравнение через дискриминант.
D = b^2 — 4×a×c
D = (-10)^2 — 4 × 1 ×(-50) = 100 + 200 = 300
√D = √300 = √100×3 = 10√3
Находим х1 и х2.
х1 = (10√3 + 10) / 2
х2 = (10√3 -10) / 2
В обоих случаях вынесем за скобку общий множитель 10.
(10√3 + 10) / 2 = 10 (√3 + 1)/2 = 5(√3 + 1)
(10√3 -10) / 2 = 10 (√3 — 1)/2 = 5(√3 — 1)
Таким образом мы нашли чему равны х. Но нам нужно найти высоту дерева, которая представлена отрезком СО.
Вспомним, что СО = х +10.
Тогда СО = 5(√3 + 1) + 10 и СО = 5(√3 — 1) + 10
Ответ: 5(√3 + 1) + 10, 5(√3 — 1) + 10.
Здание №7. Вычислите чему равна сторона b, если известно, что сторона а равна 16√2.
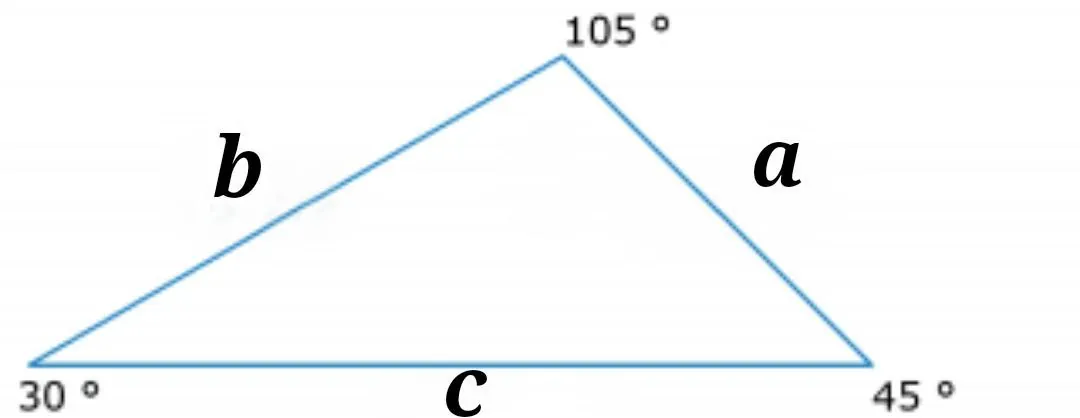
Решение. Для начала запишем все известные значения.
а = 16√2
∠А = 30°
∠В = 45°
∠С = 105°
Поскольку в этом задании нам даны все углы и лишь одна сторона, то логично будет использовать теорему синусов.
a / sinA = b / sinB = c / sinC
Таким образом, мы получим выражение a / sinA = b / sinB. Из него выразим b.
b = sinB × a / sinA
sinB = sin 45° = √2 / 2
sinA = sin 30° = 0,5
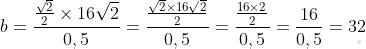
Ответ: 32
Задания для самопроверки:
Задание№1.
Найдите площадь правильного треугольника, если известно, что его периметр равен 18.
Задание№2.
Дан треугольник. Его стороны равны 8, 10 и 12. Чему равна проекция меньшей стороны на большую?
Задание№3.
Пешеход в начала прошел 300 метров на север. Затем он прошел еще 400 метров, но уже на запад. Найдите чему равно его перемещение.
Ответы:
1 — 9√3
2 — 4,5
3 — 500


