Многоугольники
Такие геометрические фигуры, как многоугольники, имеют широкие области применения в различных науках и областях жизни. Например, в архитектуре они используются для построения различных форм зданий, в компьютерной графике – для создания разнообразных объектов и анимаций и так далее. Задачи связанные с данными фигурами, конечно же, встречаются и на едином национальном тестировании. Поэтому давайте познакомимся с этой темой в математике и научимся решать задания из данного раздела, который в основном направлены на определение площадей и периметров.
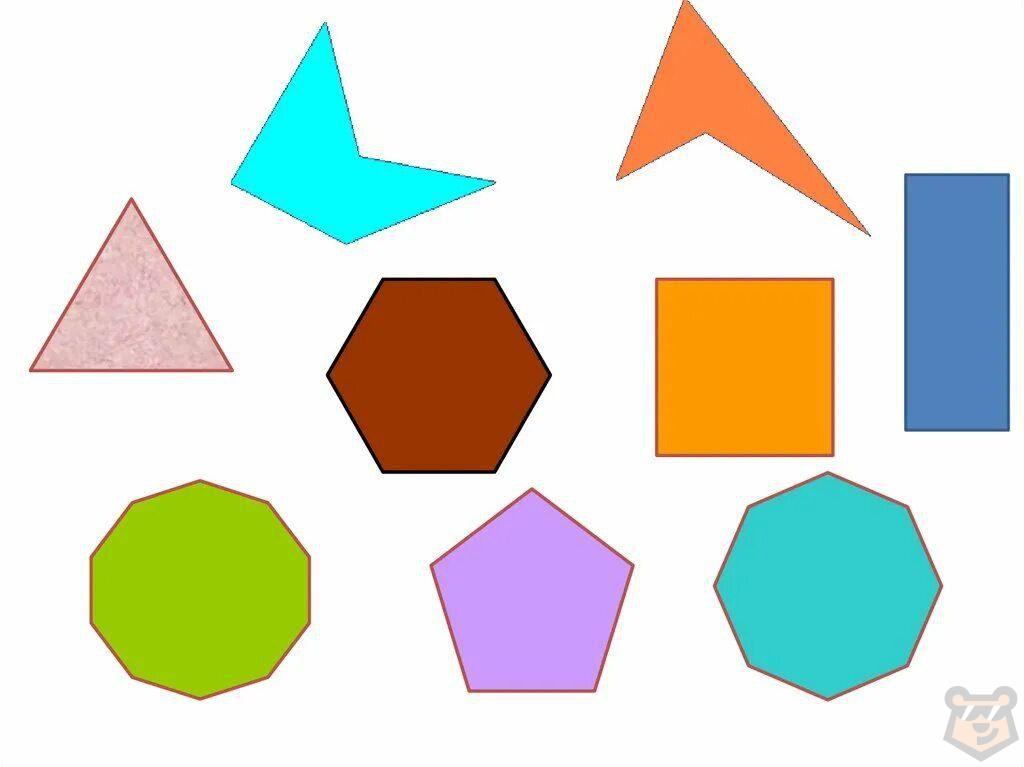
Определение.
Многоугольники – это фрагмент плоскости, который ограничен замкнутой ломаной линией.

Дары планиметрии:

Элементы многоугольника.
У многоугольников есть вершины, углы и стороны.
Вспомним!
Стороны многоугольники — это отрезки, из которых он сам и состоит.
Углы многоугольника — это углы, которые образованные его сторонами.
Вершины многоугольника — это точки, где пересекаются его стороны.
Давайте посмотрим на один чертеж и разберемся, где его вершины, углы и стороны.
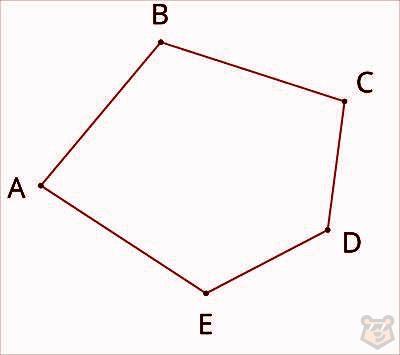
Стороны: АВ, ВС, СD, DE и EA.
Углы: АВС, ВСD, CDE, DEA и EAB.
Вершины: А, В, С, D и Е.
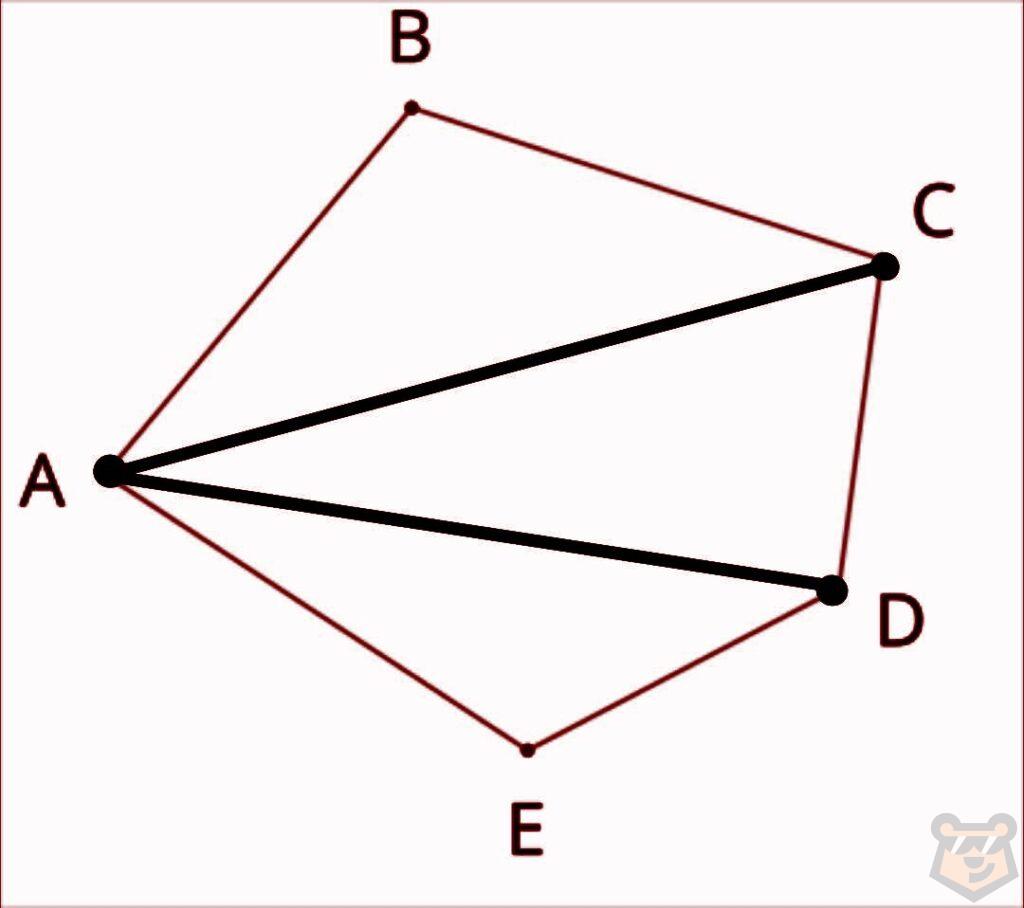
Также в многоугольниках можно провести диагонали. Вспомним! Диагонали — это отрезки, соединяющие любые две вершины фигуры, которые не являются соседними.
Например, в нашем пятиугольнике из вершины А мы можем провести только две диагонали: АС и АD. Потому что две оставшиеся вершины (В и Е) являются соседями вершины А.
История появления одного из многоугольников:

Виды многоугольников.
Существует множество видов многоугольников, каждый из которых имеет свои уникальные свойства и особенности, что делает их удивительными и интересными объектами изучения для специалистов и учащихся. Все многоугольники представлены фигурами, имеющими три и более стороны и углов. В зависимости от количества сторон, многоугольники делятся на треугольники, четырехугольники, пятиугольники и так далее. С разделами «Треугольники» и «Четырехугольники» мы уже ознакомились ранее. Теперь давайте приступим к изучению других многоугольников.
Выпуклые многоугольники.
Выпуклый многоугольник — это многоугольник, все углы которого меньше 180 градусов.
*И получается, что ни один из углов многоугольника не направлен внутрь самой фигуры.
Вогнутые многоугольники.
Вогнутый многоугольник — это многоугольник, у которого существует угол больше 180 градусов.
*То есть как минимум один из его внутренних углов направлен внутрь многоугольника.
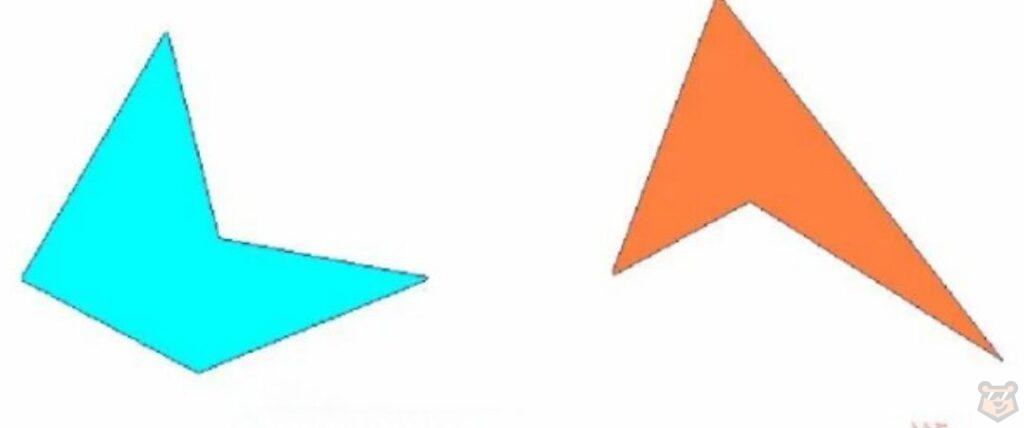
Таким образом, выпуклые и вогнутые многоугольники имеют разные свойства и отличаются внешне, а именно по направленности своих внутренних углов.
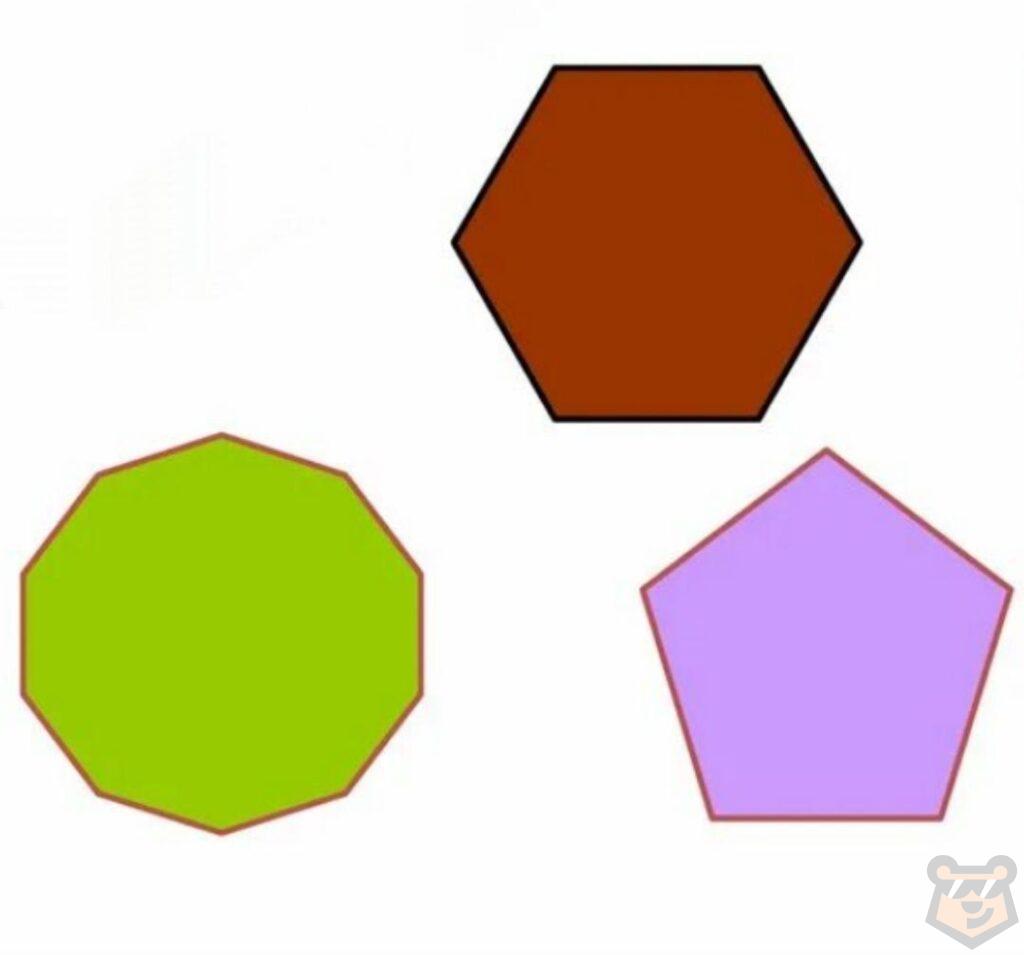
Правильные многоугольники.
Правильные многоугольники — это многоугольники, у которых все стороны и все углы равны.
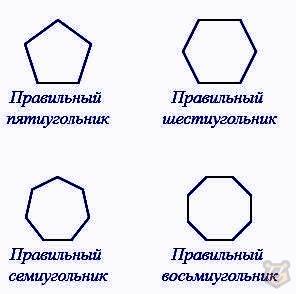
*Все правильные многоугольники являются выпуклыми.


Свойства многоугольников.
Основные свойства многоугольников включают в себя сумму углов внутри фигуры, периметр и площадь.
Углы.
Все внутренние углы выпуклого многоугольника, во-первых, меньше 180 градусов.
А во-вторых, сумма внутренних углов в n-угольнике находится по формуле: (n — 2) × 180.
А один угол правильного треугольника вычисляют с помощью следующего выражения: (n — 2) × 180 / n.
В данных формулах n — это ничто иное, как количество сторон/вершин/углов в многоугольнике.
Периметр.
Периметр многоугольника равен сумме всех его сторон.
Рn = n × a.
Площадь.
Площадь многоугольников вычисляют самыми различными способами.
1) Вычисление через радиус вписанной окружности.
S = P × r / 2.
В этой формуле Р — это периметр многоугольника, r — это радиус вписанной окружности.
2) Формула Пика.
Другим способом является формула Пика. Иногда это метод называют теоремой Пика.
*Исторический факт! Теорему назвали в честь австрийского ученого-математика, который и доказал ее правдивость ещё аж в 1899, Георга Пика
Давайте разберемся в чем заключается суть данного способа. Вычисление площади многоугольника с помощью данной формулы основывается на целочисленных вершинах.
Целочисленные вершины — это такие точки плоскости, у которых обе координаты являются целыми числами.
Сама формула выглядит следующим образом: S = В + Г/2 — 1.
В данном случае:
В — это количество целочисленных вершин внутри фигуры,
а Г — это количество целочисленных вершин на границе фигуры.
Давайте на примере одного треугольника найдем его площадь по данной формуле.
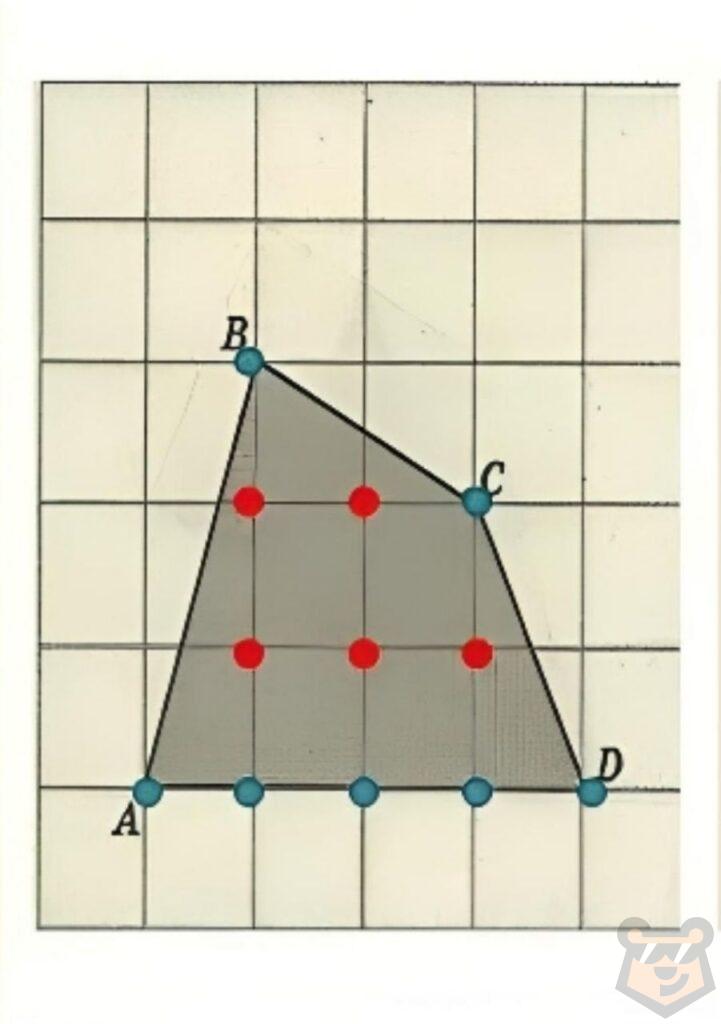
Предлагаю красным цветом отметим целочисленные точки внутри многоугольника, а синим такие точки на границе фигуры.
Тогда выйдет, что В = 5, а Г = 7. Подставляем и вычисляем.
S = В + Г/2 — 1 = 5 + 7/2 — 1 = 5 + 3,5 — 1 = 7,5 кв.ед.
*Обратите внимание на то, что формула будет справедливой лишь для таких многоугольников, чьи вершины располагаются в узлах решетки. Простым языком говоря, данные фигуры изображены на клетчатой бумаге или на клетчатом фоне.
3) Способ «разбиения».
Другим способом вычисления площади многоугольников является «разбиение» их на простые фигуры, площади которых намного легче вычислить. Допустим на треугольники, четырехугольники
Сторона правильного многоугольника.
Сторону правильного многоугольника находят по одной формуле через радиус описанной окружности.
аn = 2 × R × sin (180° / n)
Правильный шестиугольник.
*Кстати, очень часто встречаются задачи на правильный шестиугольник.
Площадь.
Именно способом «разбиения» вывели формулу для вычисления площади правильного шестиугольника, который разбили на 6 правильных треугольников. В итоге получили следующую формулу:
S = 6 × a^2√3/4 = 3 × a^2√3 / 2 = 3√3 × а^2 / 2.
S = 3√3 × а^2 / 2.
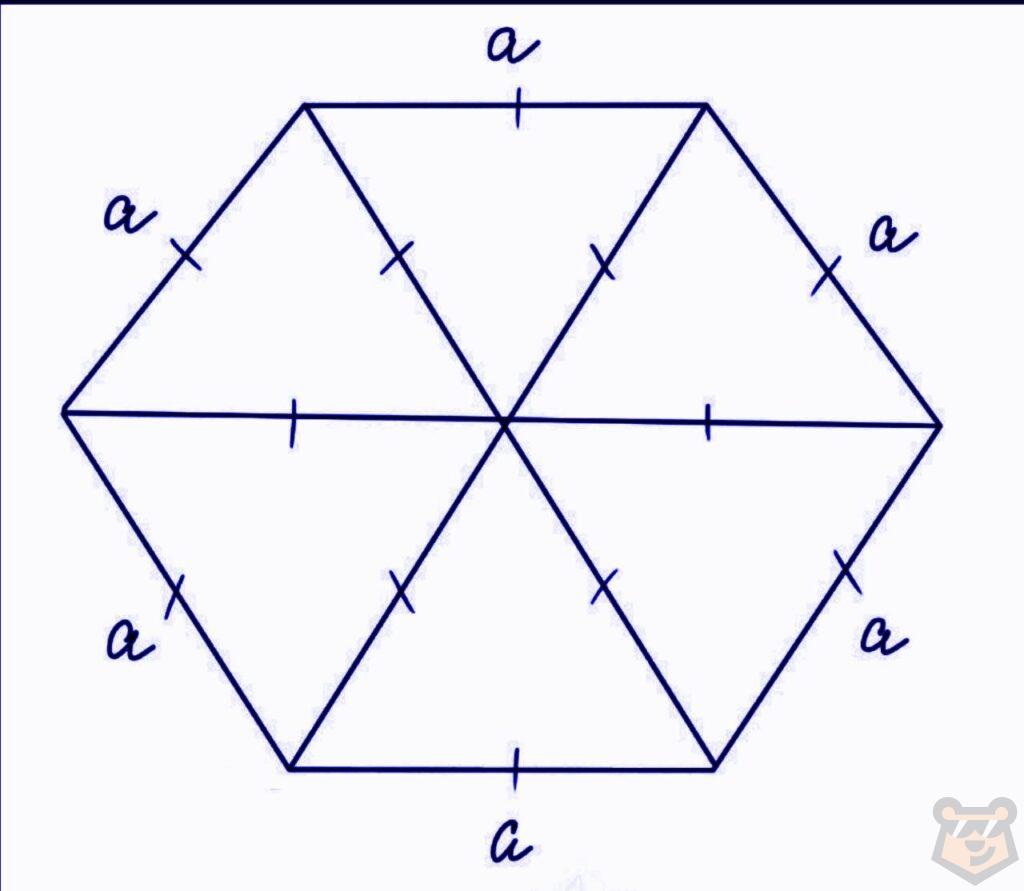
Правильный шестиугольник и радиусы вписанной и описанной окружности.
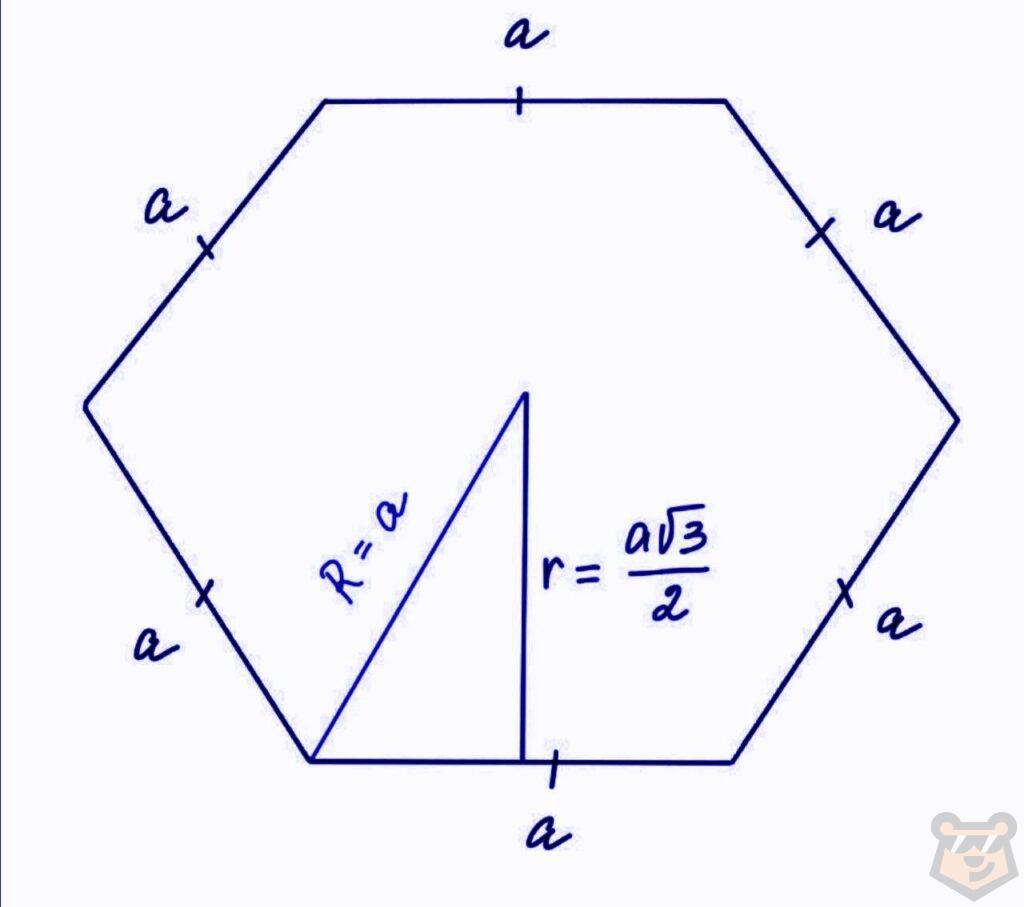
Диагонали в правильном шестиугольнике.
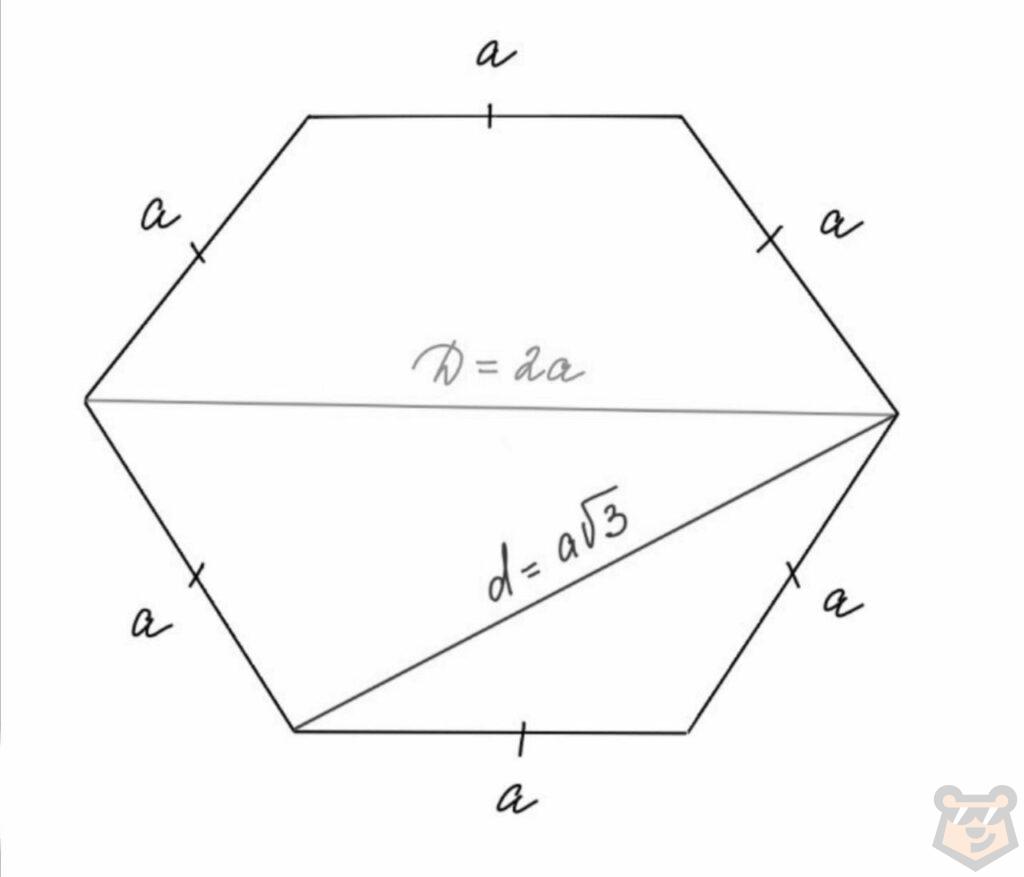
Практическая часть.
Решим несколько задач, для того чтобы закрепить пройденный материал.
Задание №1. Найдите чему равны углы правильного 9-угольника.
Решение. Используем формулу: (n — 2) × 180° / n.
Вместо n подставляем цифру 9.
(9 — 2) × 180° / 9 = 7 × 180° / 9 = = 7 × 20° = 140°
Ответ: угол равен 140°
Задание №2. Сумма четырех углов выпуклого пятиугольника равна 480°. Вычисли чему равен пятый угол фигуры.
Решение. Для начала найдем сумму внутренних углов пятиугольника. Для этого будем использовать формулу: (n — 2) × 180°.
На место n ставим цифру 5 и делам вычисления.
(5 — 2) × 180° = 3 × 180° = 540°
Мы нашли сумму всех внутренних углов. Теперь отнимем от нее сумму четырех углов и найдем градусную меру недостающий угла.
540° — 480° = 60°
Ответ: 60°.
Задание №3. Найдите чему равна сторона правильного шестиугольника, если известно, что его площадь равняется 12√3.
Решение. Для того чтобы вычислить сторону фигуры, будем использовать формулу S = 3√3 × а^2 / 2.
Подставляем вместо S значение площади и решаем.
1) 12√3 = 3√3 × а^2 / 2
2) 12√3 × 2 = 3√3 × а^2
3) 24√3 = 3√3 × а^2
4) 24√3 / 3√3 = а^2
5) 8 = а^2
6) а = √8
а = 2√2
Ответ: √8 или 2√2.
Задание по данному разделу, которые встречаются на ЕНТ.
Задачи по теме «Многоугольники» на едином национальном тестировании присутствуют в профильной математике. В разделе же «математическая грамотность» в основном встречаются задания по темам «Треугольники» и «Четырехугольники».
Задание №1. Найдите сколько вершин в правильном многоугольнике, если градусная мера его углов составляет 160.
Решение. Воспользуемся формулой (n — 2) × 180° / n.
Приравняем данное выражение к 160°.
(n — 2) × 180° / n = 160°
(n — 2) × 180° = 160° × n
В итоге получим уравнение: 180n — 360 = 160n
Решим его.
180n — 160n = 360
20n = 360
n = 360/20
n = 18
Ответ: 18 вершин.
Задание №2. Вычислите чему равна площадь правильного шестиугольника, сторона которого равна 6. Радиус вписанной окружности равен 3√3.
Решение. Вспомним формулу S = P × r / 2.
Вычислим сначала периметр фигуры.
Рn = n × a. Р6 = 6 × 6 = 36.
Теперь подставим наши значения в первую формулу.
S = 36 × 3√3 / 2 = 54√3
Ответ: 54√3
Задание №3. Вычислите чему равен периметр правильного многоугольника, в котором все углы равны по 135 градусов. Известно, что диаметр описанной окружности равен 10,46.
Решение. Для того чтобы вычислить периметр фигуры, в начале необходимо определить вид треугольника и найти его сторону. Для этого воспользуемся формулами: (n — 2) × 180° / n и аn = 2 × R × sin (180° / n).
1) (n — 2) × 180° / n = 135°
2) (n — 2) × 180° = 135° × n
3) 180°n — 360° = 135°n
4) 180°n — 135°n = 360°
5) 45°n = 360°
6) n = 360° / 45°
7) n = 8
Теперь преобразуем нашу формулу используя для этого взаимосвязь радиуса с диаметром.
D = 2 × R
Получается вместо 2R в формуле мы можем подставить D.
аn = D sin180° / n
Подставляем наши значения в формулу.
а8 = 10,46 sin180°/8 = 10,46 × sin 22,5 = 10,46 × 0,383 = 4,0029 ≈ 4
Выходит, что все стороны в нашем в восьмиугольнике равны 4.
Используем формулу и вычислим периметр фигуры: Рn = n × a.
Р8 = 8 × 4 = 32
Ответ: 32.
Задания для самопроверки:
Задание№1.
Вычислите площадь фигуры воспользовавшись чертежом, представленным ниже.

Задание №2.
Найдите чему равна градусная мера последнего угла в десятиугольнике, если сумма других девяти углов равняется 1303 градусам.
Задание №3.
Найдите чему равна площадь шестиугольника, используя данный чертеж.
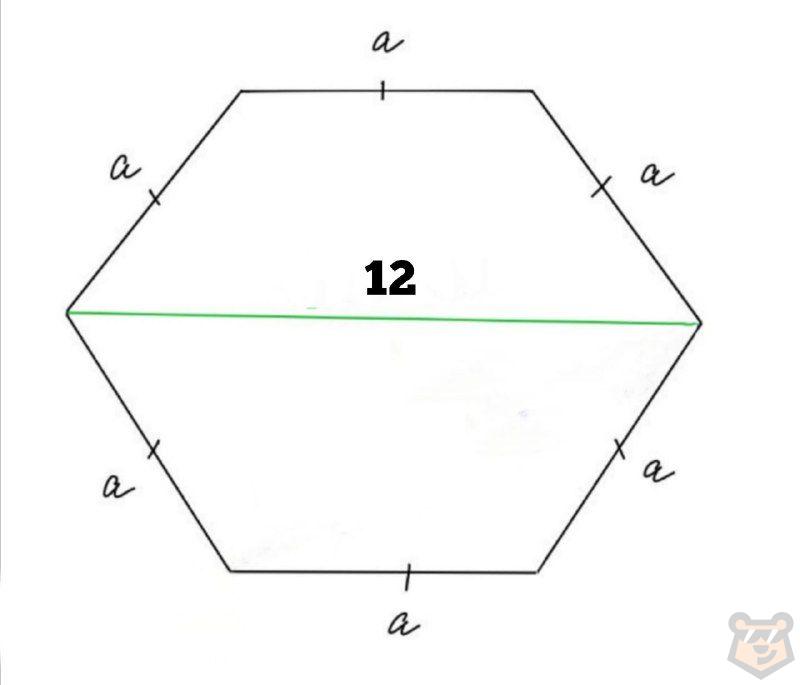
Ответы:
1 — 10 кв.ед.
2 — 137°.
3 — 54√3 кв.ед.

