Четырехугольники
Одним из самых больших и объемных разделов планиметрии являются четырехугольники. Есть разные виды данных фигур, которые отличаются и визуально, и своими свойствами. Умение работать с различными четырехугольниками пригодиться не только при решении задач, но и в реальной жизни. Например, с помощью изучения и понимания данной темы мы можем найти сколько необходимо закупить рулонов обоев или сколько используется плиток в ванной для ремонта. В общем применение наших теоретических знаний на практике очень велико. Кроме этого стоит понимать, что такой раздел, конечно же, встречается и на ЕНТ. Поэтому давайте ознакомимся с данной темой.
Четырехугольники, что это ?
Четырехугольники — это фигуры, у которых, естественно, есть 4 угла и 4 стороны.
Вершинами в данном случае будут являться 4 точки.
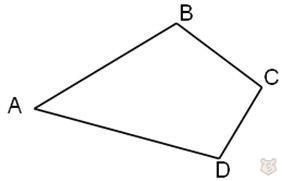
У четырехугольников есть по две диагонали. Диагонали — это отрезки, соединяющие противолежащие углы.
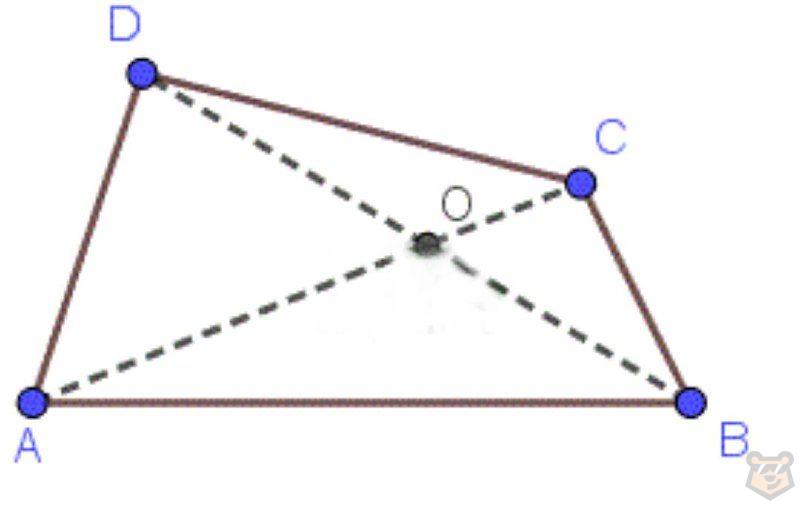
В четырехугольнике АВСD диагоналями являются отрезки АС и BD.
Сумма внутренних углов четырехугольников.
Давайте для того, чтобы понять чему равна сумма всех внутренних углов данных фигур, проведем одну диагональ.
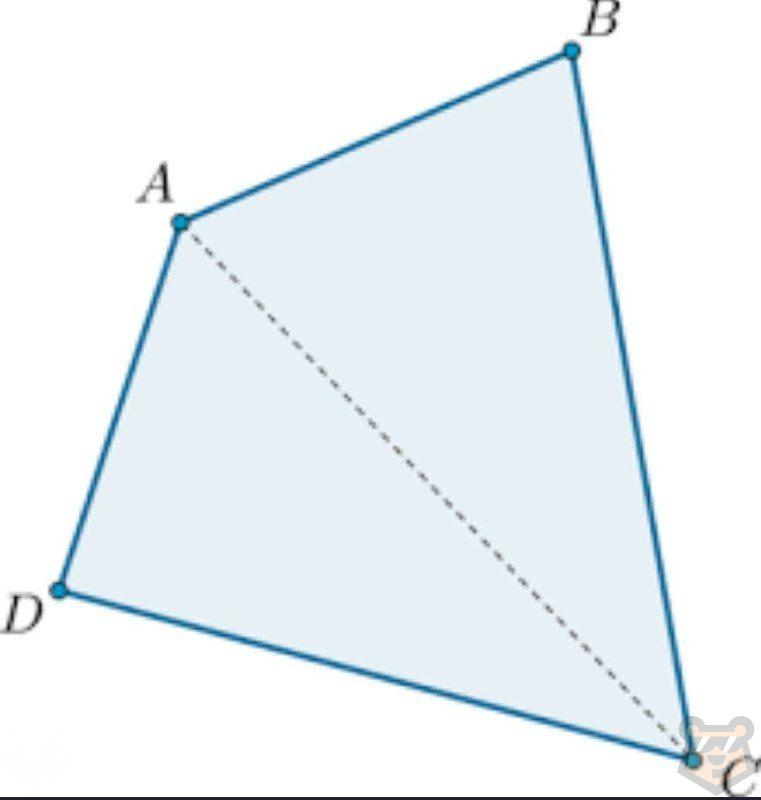
Наша диагональ разделила данный четырехугольник на два треугольника. Мы помним, что сумма внутренних углов треугольника равна 180 градусов. А сумма углов двух треугольников равна 360 градусов.
180° × 2 = 360°
Таким образом, сумма внутренних углов четырехугольников всегда равна 360°.

Сумма внешних углов четырехугольников
Учитывая то, что внешние углы это смежные углы со внутренними, то мы получим 4 развернутых угла. Один развернутый угол равен 180°. А 4 таких угла равны 720°.
180° × 4 = 720°
Тогда значение только внешних углов найдем отняв 360 от 720.
720° — 360° = 360°
Сумма внешних углов четырехугольников всегда равна 360°.
Это самые основные и общие признаки четырехугольника. Но есть разные виды таких фигур. Каждый тип необходимо изучить по отдельности.
Виды четырехугольников.
Квадрат.
Знакомая фигура еще с начальных и дошкольных классов. Любимый четырехугольник у многих учеников. Потому что он отличается своей простотой.
Квадрат — четырехугольник, имеющий 4 равных сторона и 4 угла по 90 градусов.
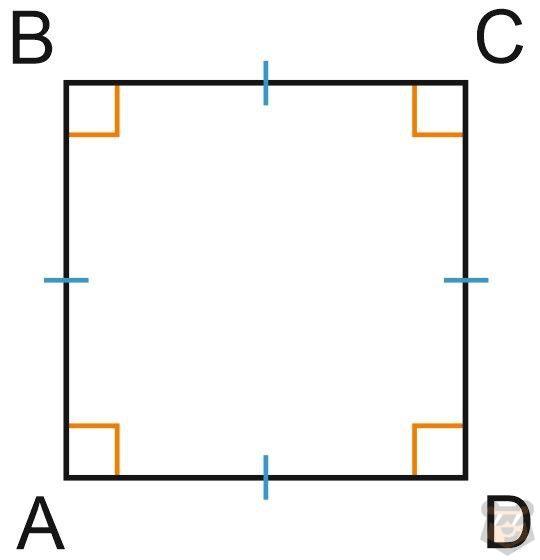
АВ = ВС = СD = DA
∠A = ∠B = ∠C = ∠D = 90°
Диагонали в квадрате.
Диагонали в квадрате равны, пересекаются под прямым углом. В точке пересечения делятся пополам. А также являются биссектрисами.
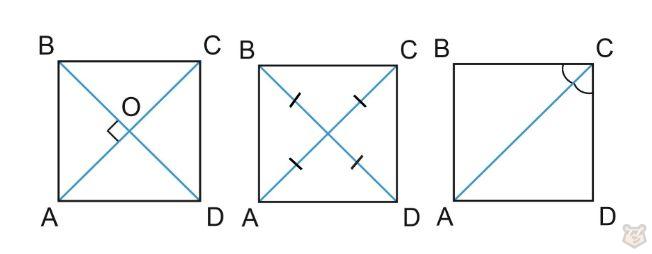
Кроме того диагональ и сторона квадрата взаимосвязаны формулой: d = a √2.
Площадь квадрата.
Площадь квадрата находится по двум формулам
1) Через сторону.
S=a^2
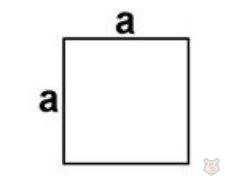
2) Через диагональ.
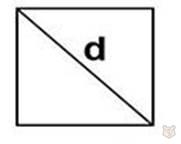
S = d^2 / 2
Периметр квадрата.
Вспомним, что периметр — это сумма длин всех сторон.
Получается, что периметр квадрата это сумма четырех его одинаковых сторон.
Р = а + а + а + а
Р = 4а
Прямоугольник.
Еще одна узнаваемая фигура.

Прямоугольник — это четырехугольник, у которого две стороны попарно равны и параллельны, углы в нем равны по 90 градусов.
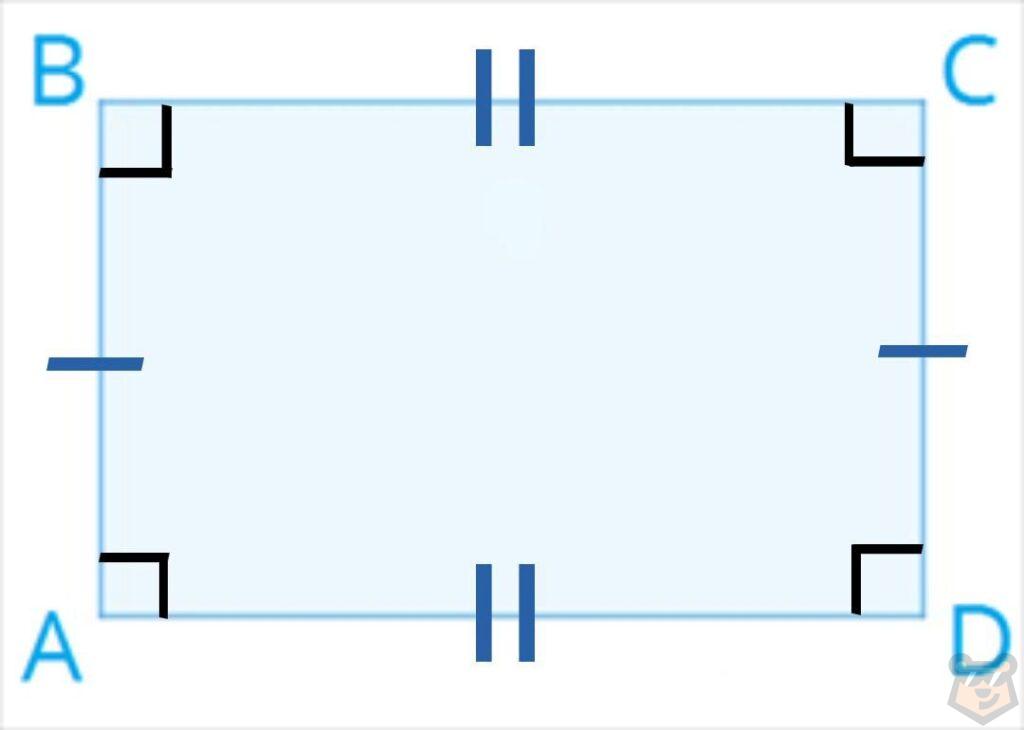
АВ = CD, AC = CD
АВ II CD, AC II CD
∠A=∠B=∠C=∠D=90°
Диагонали в прямоугольнике.
Диагонали в прямоугольнике равны и в точке пересечения делятся пополам.
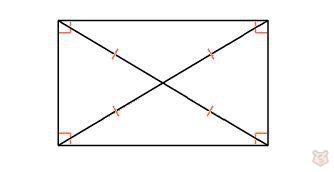
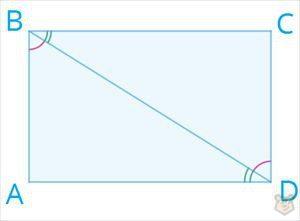
Также диагональ делит прямоугольник на два равных треугольника, в которых является гипотенузой. Кроме того углы, которые образуются при проведении диагоналей, будут накрест равны. Потому что являются внутренними накрест лежащими.
Площадь прямоугольника.
Площадь прямоугольника находится по двум формулам.
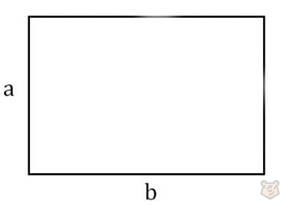
1) Через две стороны.
S=ab
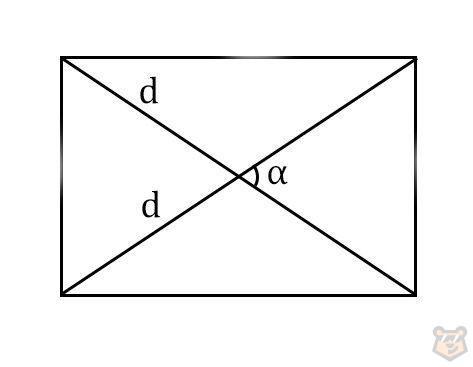
2) Через диагонали и синус образованного ими угла.
S = d^2 / 2 × sinA
Периметр прямоугольника.
Согласно определению периметра, нам необходимо сложить 2 длины и 2 ширины.
P = a + a + b + b
P = 2a + 2b
P = 2 (a + b)
Параллелограмм.
Параллелограмм — это такой четырехугольник, в котором стороны попарно равны и параллельны.
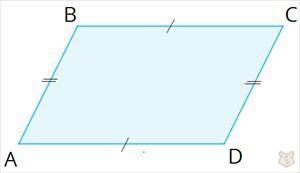
АВ=CD, AC=CD
АВ II CD, AC II CD
Он отличается от прямоугольника тем, что его углы не равны 90 градусам. Также в параллелограмме противолежащие углы равны. А сумма углов принадлежащей одной стороне равняется 180 градусам.
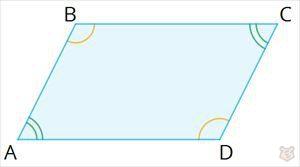
∠А =∠С , ∠B = ∠D
∠A + ∠B = ∠B + ∠С = ∠С + ∠D = ∠D + ∠A = 180°
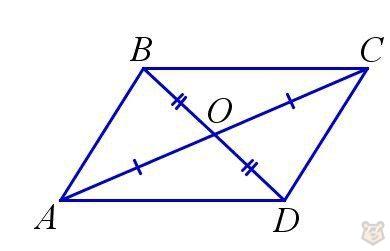
Диагонали в параллелограмме.
Диагонали в параллелограмме в точке, где пересекаются, делятся пополам.
Углы, которые образуются при проведении диагоналей, будут накрест равны. Потому что являются внутренними накрест лежащими.
Площадь параллелограмма.
Площадь параллелограмма находятся с помощью нескольких формул.
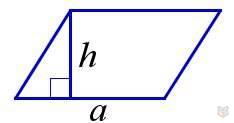
1) Через сторону и проведенную к ней высоту.
S = а × h
2) Через две разные стороны и синус острого угла между ними.
S = a × b × sinA
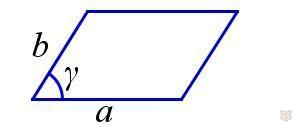
3) Через диагонали и синус образованного ими угла.
S = ( d1 × d2 ) / 2 × sina
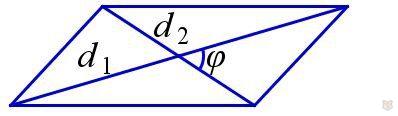
Периметр параллелограмма.
Аналогичная с прямоугольником ситуация.
P = 2 (a + b)
Ромб.
Ромб — это четырехугольник, у которого стороны попарно параллельны, а также все равны.
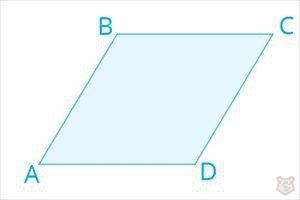
АВ = ВC = CD = DА
АВ II CD, AC II CD
Противоположные углы ромба также равны.
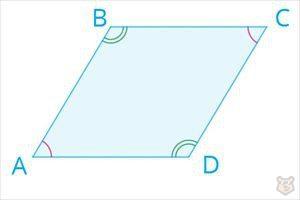
∠А =∠С , ∠B = ∠D
Углы принадлежащие одной стороны равны 180 градусам.
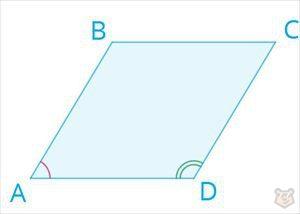
∠A + ∠B = ∠B + ∠С = ∠С + ∠D = ∠D + ∠A = 180°
Диагонали в ромбе.
Диагонали в ромбе пересекаются под углом в 90 градусов, а также в точке пересечения они делятся пополам. Кроме того диагонали являются биссектрисами углов.
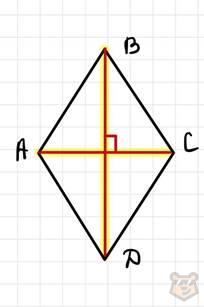
AC ⊥ BD
∠ADB = ∠BDС, ∠DСА = ∠ВСА и так далее.
Площадь ромба.
Существует несколько формул для нахождения площади ромба.
1) Через сторону и проведенную к ней высоту.
S = а × h
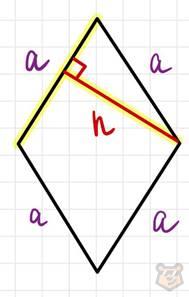
2) Через две диагонали.
S = d1 × d2 / 2
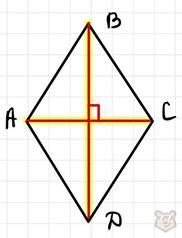
3) Через сторону и синус острого угла.
S = a^2 × sinA
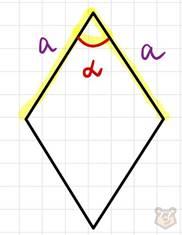
Периметр ромба.
С учетом того, что у ромба 4 одинаковых стороны формула периметра примет такой же вид, как и у квадрата.
Р = 4а.
Трапеция.
Трапеция — это четырехугольник, у которого две стороны параллельны.
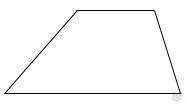
АВ II CD
Две параллельные стороны принято называть основаниями. А две другие являются боковыми сторонами.
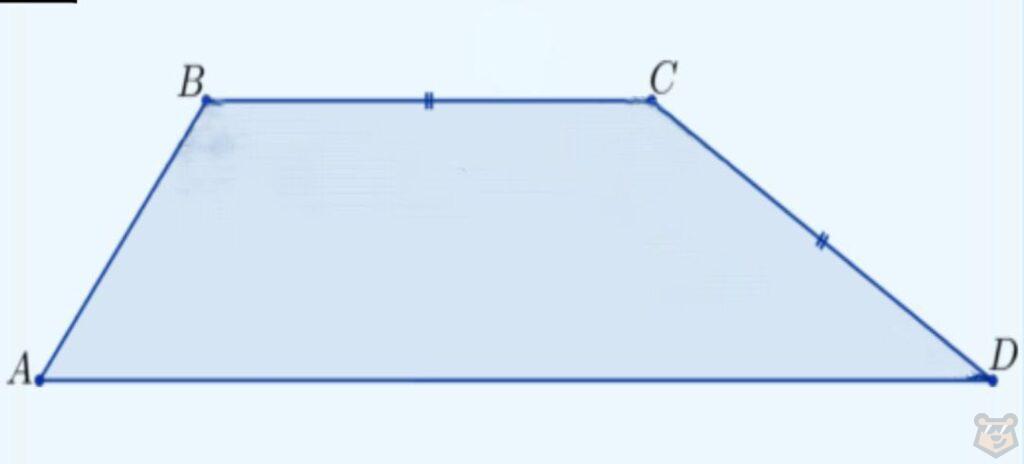
АВ и CD — основания, AC и CD — боковые стороны.
Углы, принадлежащие боковым сторонам в сумме дают 180 градусов.
∠А + ∠С = ∠В + ∠D = 180°
В трапециях также проводят среднюю линию.
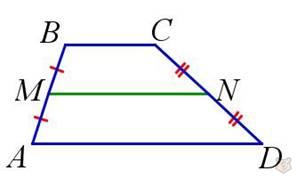
Средняя линия — это такой отрезок, который соединяет середину двух боковых сторон.
Средняя линия равна полусумме оснований.
MN = (BC + AD) / 2
Виды трапеций.
1) Прямоугольная трапеция.
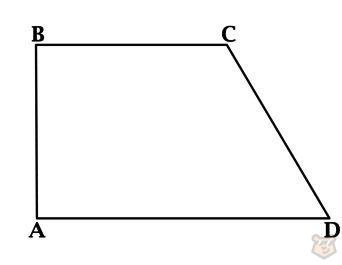
Трапеция, где есть два прямоугольных угла, которые находятся между боковой одной стороной и основаниями, называется прямоугольной.
∠А = ∠С = 90°
2) Равнобедренная трапеция.
Трапеция, у которой две боковые стороны равны, является равнобедренной.
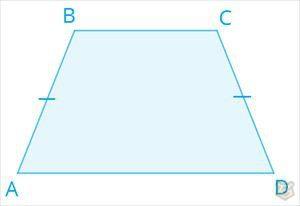
АС = ВD
В равнобедренной трапеции углы при основаниях равны.
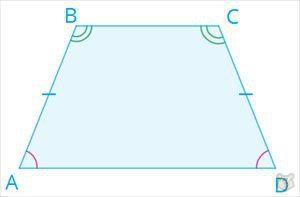
∠А = ∠В, ∠С = ∠D
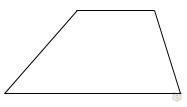
3) Произвольная трапеция.
Произвольная трапеция — это любая другая трапеция, которая не является ни равнобедренной, ни прямоугольной.
Площадь трапеции.
Площадь трапеции можно найти с помощью нескольких формул.
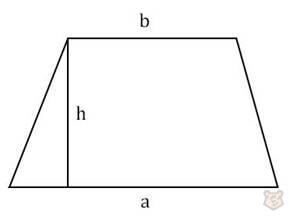
1) Через высоту и основания.
S = (a+b)/2 × h
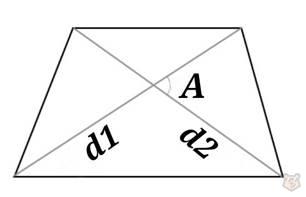
2) Через диагонали и синус образованного ими угла.
S = d1 × d2 / 2 × sinA
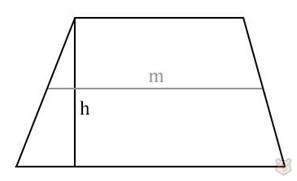
3) Через среднюю линию и высоту.
S = m × h
Периметр трапеции.
Для нахождения периметра трапеции нужно будет просто сложить все ее стороны.
Заключительная таблица.
Основные свойства и площадь четырехугольников.
| Название | Свойства | Площадь |
Квадрат |  | |
Прямоугольник | 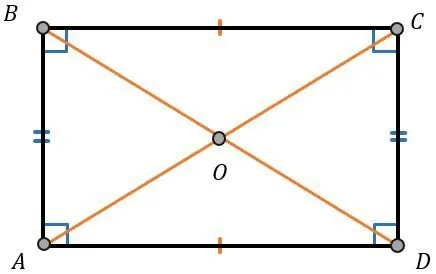 | |
Параллелограмм | 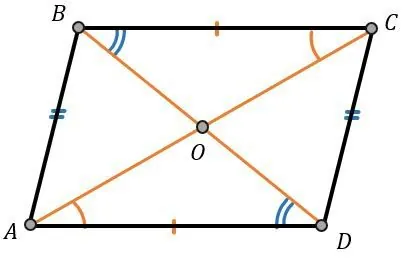 | |
Ромб | 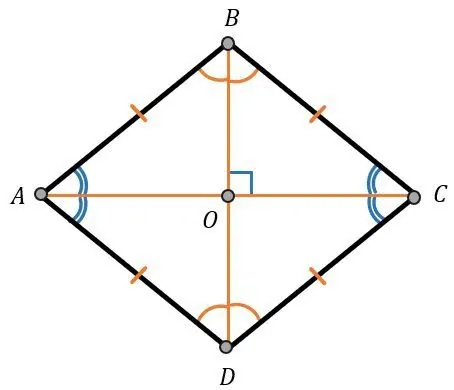 | |
Трапеция | 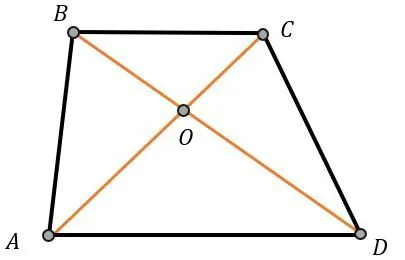 |
Думаю, самые внимательные заметили, что квадрата совмещает в себе свойства и прямоугольника, и параллелограмма, и ромба.
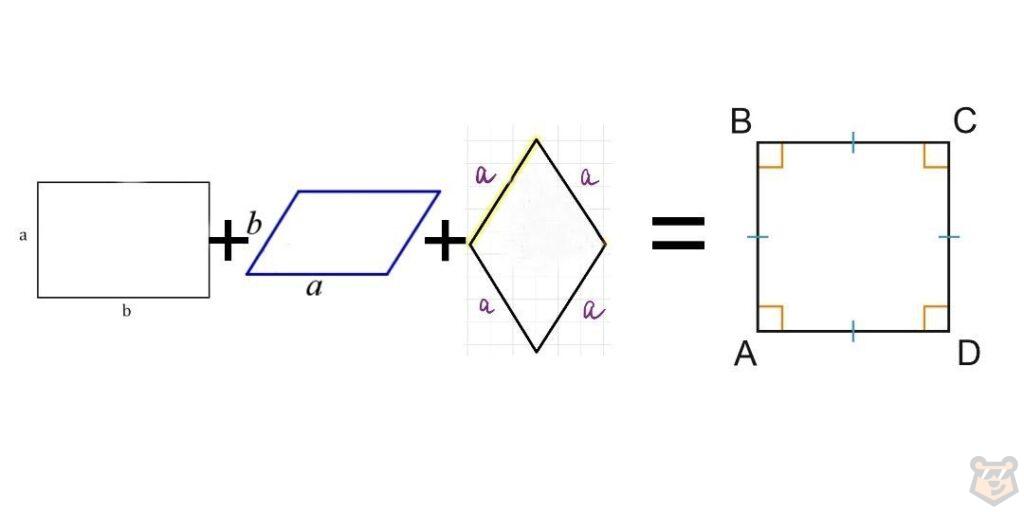
| Свой среди чужих | Чужой среди своих |
 |  |
Практическая часть.
Задание№1. Найдите площадь представленной на чертеже фигуры. Длина одной клеточки равна 2 см.
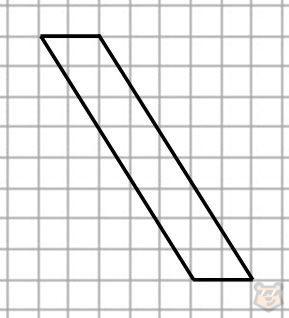
Решение. Данная фигура является параллелограммом. Мы можем легко по клеточкам определить чему равна одна его сторона и проведенная к ней высота. Значит будем использовать формулу S = а × h.
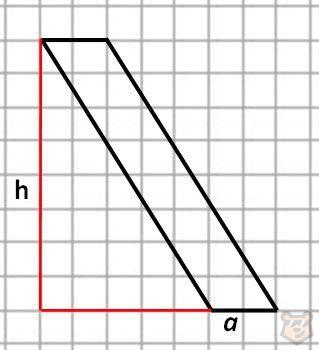
Сторона представлена 2 клеточками.
Высота состоит из 8 клеточек.
а = 2 × 2 см = 4 см
h = 8 × 2 cм = 16 см
S = а × h = 4 см × 16 см = 64 см^2
Ответ: 64 см^2
Задание№2. Используя рисунок найдите сумму двух острых углов данной трапеции.
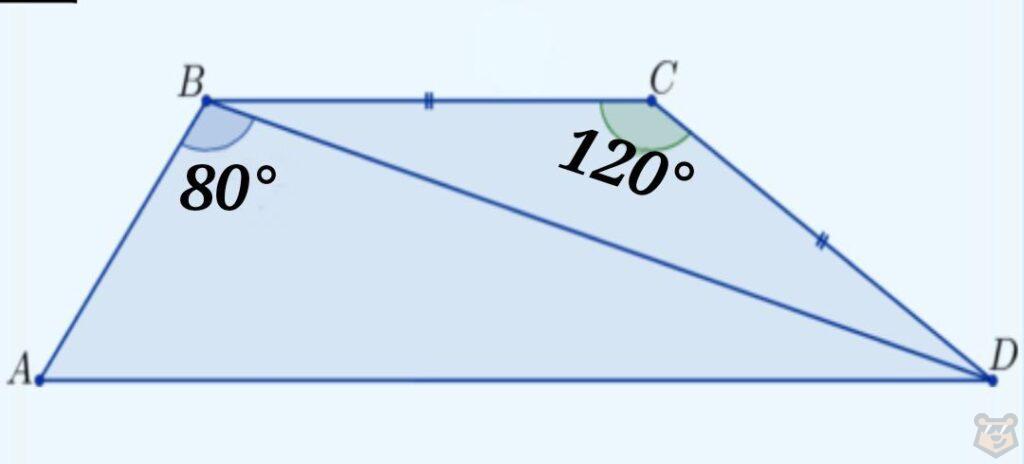
Решение. Выходит, что нам нужно найти ∠CDA = ∠ВАD.
Во-первых, по графику видно, что ∠CDA = ∠CDB + ∠ВDA.
Во-вторых, согласно свойствам треугольника ∠ВАD = 180° — ∠ABC.
И теперь отталкиваясь от этого будем решать.
1) Согласно графику ВC = СD. Тогда получается, что ∠СВD = ∠CDВ.
2) Найдем чему равны данные углы благодаря тому, что мы знаем чему равняется сумма внутренних углов треугольника.
∠А + ∠В + ∠С = 180°
∠ВСD + ∠СВD + ∠CDВ = 180°
2.1. Представим углы СВD и CDВ как х.
2.2. 120° + х + х = 180°
120° + 2х = 180°
2х = 180° — 120°
2х = 60°
х = 30°
2.3. Тогда ∠СВD = ∠CDВ = 30°.
2.4. В таком случае ∠ABC = ∠АВD + ∠СВD = 80° + 30° = 110°.
3) Теперь зная, что сумма углов принадлежащих боковым сторонам равна 180°, найдем угол ∠ВАD
∠ВАD = 180° — ∠ABC = 180° — 110° = 70°
4) Сейчас внимательно посмотрев на треугольник АВD, найдем угол ВDA.
∠ВDA = 180° — ∠ВАD — ∠ABC = 180° — 70° — 80° = 30°
Таким образом, ∠CDA = ∠CDB + ∠ВDA= 30° + 30° = 60°
5) Наконец найдем сумму углов CDA и ВАD.
∠CDA = ∠ВАD = 70° + 60°= 130°
Ответ: 130°.
Задания по данному разделу, которые встречаются на ЕНТ.
Задачи по теме «Четырехугольники» встречаются как в разделе «математическая грамотность», так и профильной математике. Для того чтобы не потерять баллы, давайте рассмотрим основные типы заданий, присутствующих на едином национальном тестировании.
Математическая грамотность.
Задание№1. Большой прямоугольник разделили на 9 равных прямоугольников. Найдите площадь большой фигурой, если длина маленького прямоугольника равны 15 см.

Решение. Площадь прямоугольника находится по формуле S = ab.
Нам необходимо найти две стороны большого прямоугольника а и b.
Обязательно учитываем то, что все маленькие прямоугольники равны.
Обратим внимание на то, что одна сторона большого прямоугольника состоит из двух длин маленького прямоугольника.
y = 15, тогда получается, а = у + у = 15 + 15 = 30.
а = 30 см
Вторая сторона состоит из одной длины и двух ширин маленького прямоугольника.
Вспомним, что все прямоугольники у нас равны значит, что сумма пяти ширин у нас равно сумме двух длин.
Учитывая, что а = 30, то сумма 5 ширин равна 5х.
Приравниваем 5х и 30.
5х = 30
х = 6.
Теперь найдем сторону b.
b = у + x + x = 10 + 6 + 6 = 22
Теперь найдем площадь по формуле S = ab.
S = ab = 22 × 30 = 660 см^2
Ответ: 660 см^2
Задание№2. Площадь закрашенного части прямоугольника равна 24. Найдите чему равен его периметр если известно, что одна сторона прямоугольника больше другой в 3 раза.

Решение. Периметр прямоугольника находим по формуле Р = 2 ( а + b). А это значит нам нужно найти а и b.
Для этого вспомним формулу площади прямоугольника. S = a × b
Учитывая то, что диагональ в прямоугольнике делит его на два равных треугольника, можно легко найти площадь самого прямоугольника.
SABCD = 2 × SABC
SABCD = 2 × 24 = 48
Получается, что a × b = 48.
Вспомним, что сторона одна в три раза больше другой.
Пусть наш b будет х.
Тогда а будет 3х.
Получается, a × b = х × 3х = 3 х^2
Выходит, что 3 х^2 = 48.
Решим уравнение 3х^2 = 48.
х^2 = 48 / 3
х^2 = 16
х = √ 16
х = 4
Значит, b = 4.
Тогда а = 3 × х = 3 × 4 = 12. b = 4, a = 12.
Теперь найдем периметр.
Р = 2 × (4 +12) = 2 × 16 = 32
Ответ: 32.
Математика.
Задание№1. Найдите площадь квадрата если его диагональ равна √288.
Решение. Площадь находят через формулу S = a^2. Выходит, что нам нужно найти чему равна сторона квадрата.
Для этого вспомним формулу d = a × √2. Выразим из нее сторону квадрата. а = d / √2.
Представим √288 чуть по-другому.
√288 = √ (2 × 144)
Вынесем 144 из-под корня. И получим:
12√2.
а = d / √2 = 12√2 / √2 = 12
S = a^2 = 12^2 = 144
Ответ: 144.
Задание№2. Найдите сторону ромба, если его диагонали относятся как 6 : 8, а площадь равна 216.
Решение. Найдем произведение наших диагоналей используя формулу площади ромба: S = d1 × d2 / 2
Выходит, что d1 × d2 / 2 = 216.
Тогда d1 × d2 = 432.
Теперь представим d1 как 6х, а d2 представим как 8х. Получим: 6х × 8х = 432
Решим уравнение.
48х^2 = 432
х^2 = 432 / 48
х^2 = 9
х = √9
х = 3
Вспомним, что d1 = 6x, a d2 = 8x.
d1 = 6x = 6 × 3 = 18
d2 = 8x = 8 × 3 = 24
Теперь вспомним, что в точке пересечения диагонали делятся пополам. Тогда:
d1 / 2 = 18 / 2 = 9
d2 / 2 = 24 / 2 = 12
Сторону а найдем с помощью теоремы Пифагора.
с^2 = а^2 + b^2
c^2 = 9^2 + 12^2 = 81 + 144 = 225
c^2 = 225
c = √ 225
c = 15
Ответ: 15.
Задание№3. Два основания в прямоугольной трапеции равняются 1 и 4 метрам. Ее площадь равна 7,5 метров. Найдите высоту и острый угол этой трапеции.
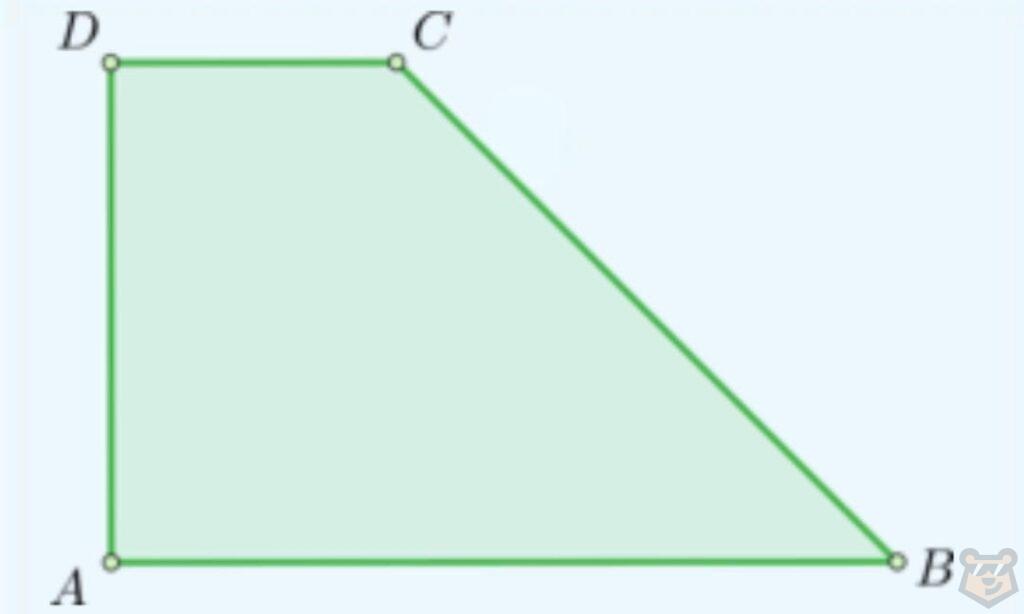
Решение. Необходимо найти высоту и угол В.
Для этого проведем высоту СН. Тем самым мы отсечем на отрезке АВ два других отрезка АН и НВ.
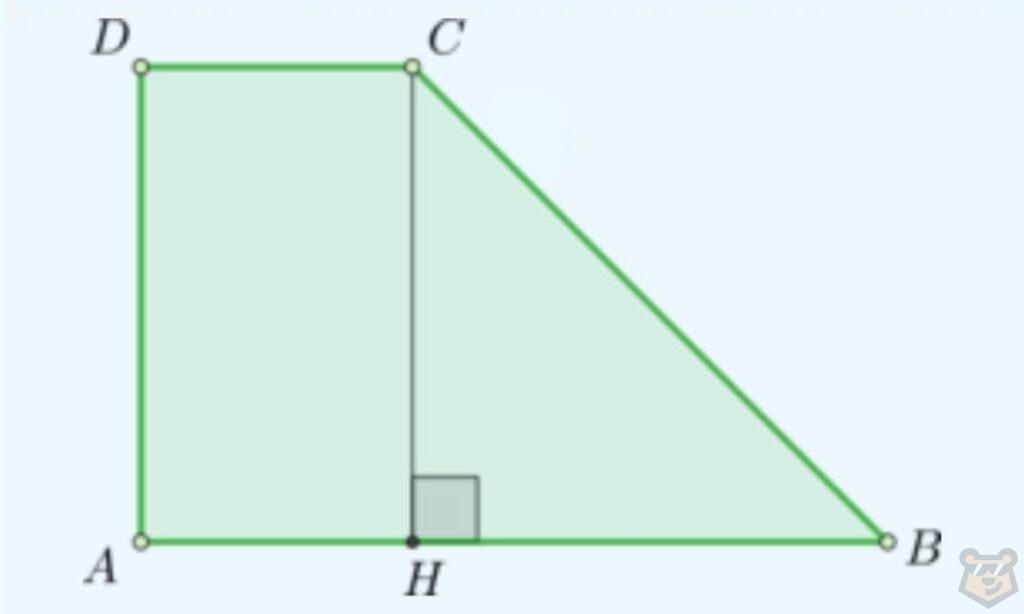
Заметим, что АDCH это прямоугольник. Тогда AH = DC = 1 м.
В таком случае НВ = АВ — АН = 4 — 1 = 3 м.
Теперь найдем высоту через площадь, которую вычисляют по формуле S = (a+b)/2 × h.
(a+b)/2 × h = 7,5
Подставим вместо а и b наши основания.
(1 + 4) / 2 × h = 7,5
5 / 2 × h = 7,5
2,5 × h = 7,5
h = 3
Получается, что СН = 3.
Заметим, что СН = НВ = 3.
Тогда треугольник СНВ является равнобедренным. И в таком случае ∠С = ∠В.
Посмотрим на угол Н. ∠Н = 90.
Представим ∠С и ∠В как х. И учитывая то, что сумма внутренних углов треугольника всегда равняется 180°, найдем чему равен угол В.
90° + х + х = 180°
90° + 2х = 180°
2х = 180° — 90°
2х = 90°
х = 90° / 2
х = 45°
Тогда ∠В = 45°.Ответ: 3 м, 45°.
Задания для самопроверки:
Задание№1.
Стороны прямоугольника равны 9 и 4 см. Найдите сторону квадрата, который будет равновелик данному прямоугольнику.
Задание№2.
Чему равна площадь ромба если одна из его диагоналей равна 16, а вторая в 2 раза меньше ?
Задание№3.
Высота трапеции равняется 7м. Полусумма ее оснований равна 5м. Чему равна площадь данной фигуры.
Ответы:
1 — 6 см
2 — 64
3 — 35 м^2


