Производная
Производная функции является мощным методом анализа и исследования функций, который находит применение в различных областях науки и техники. Производная играет важную роль не только в математике и прикладных к ней науках, но и в физике, экономике, где она помогает моделировать различные процессы и явления.
Она используется для определения экстремумов функций, нахождения точек перегиба, исследования поведения графиков функций и многих других задач.
Давайте разберемся что же такое “производная”и с чем ее принято “кушать”.
Производной называют такой предел, который является отношением приращения самой функции (у) к приращению ее аргумента (х), когда приращение аргумента стремится к нулю. ( если такой предел может существовать.)
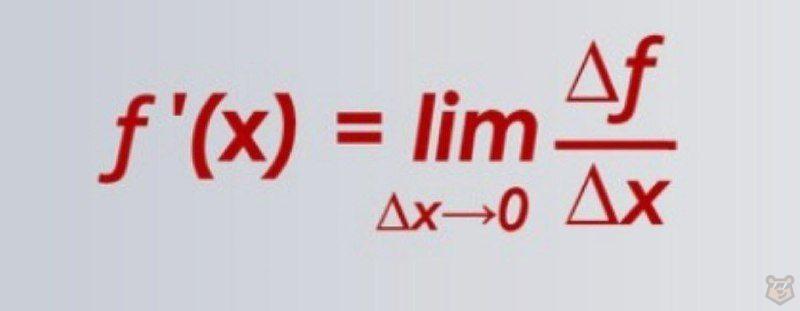
Думаю такое определение и его математическое отражение мало кому может что-либо объяснить, ну разве что мы поймем как отмечается производная ( f’ (x) ). Поэтому выразимся более простым и понятным языком.
Производная обозначает скорость изменения функции в какой-либо одной конкретной точке.
Само вычисление производной называют дифференцированием. Для нахождения производных необходимо ознакомиться со следующими таблицами, где представлены все нужные формулы и правила дифференцирования, которые мы будем использовать при решении заданий. Их желательно выучить, ведь не везде можно использовать шпаргалку.
Таблица производных
| f (x) функция | f’ (x) производная функции |
| С (константа, абсолютно любое число) | 0 |
| х | 1 |
| х^n | n×x^(n-1) |
| √x | 1/2√x |
| 1/x | -1/x^2 |
| sinx | cosx |
| cosx | -sinx |
| tgx | 1/cos^2x |
| ctgx | — 1/sin^2x |
| e^x | e^x |
| a^x | a^x×lna |
| lnx | 1/x |
| logx | 1/x×lna |
Правила дифференцирования
| (u+v)’ | u’+v’ |
| (u-v)’ | u’-v’ |
| (u×v)’ | u’×v + v’×u |
| (u/v)’ | (u’×v — v’×u)/v^2 |
| (c×f)’ | c×f’ |
u, v, и f в данных формулах выступают в роли функций, а с является константой (или же абсолютно любым числом).
Обратимся к одному примеру для того, чтобы лучше понять суть самой производной и научиться правильно применять формулы.
Первоклассник решил улучшить свою технику чтения. Первую неделю он читал только 34 слова в день. Начиная со второй недели он стал каждый день читать на 2 слово больше.
1) Составим функцию, которая описала бы первую неделю занятий. Получим: у=34. Нет необходимости составлять таблицу, ведь при любом значении х, наш у всегда будет равен только 34. Начертим график.
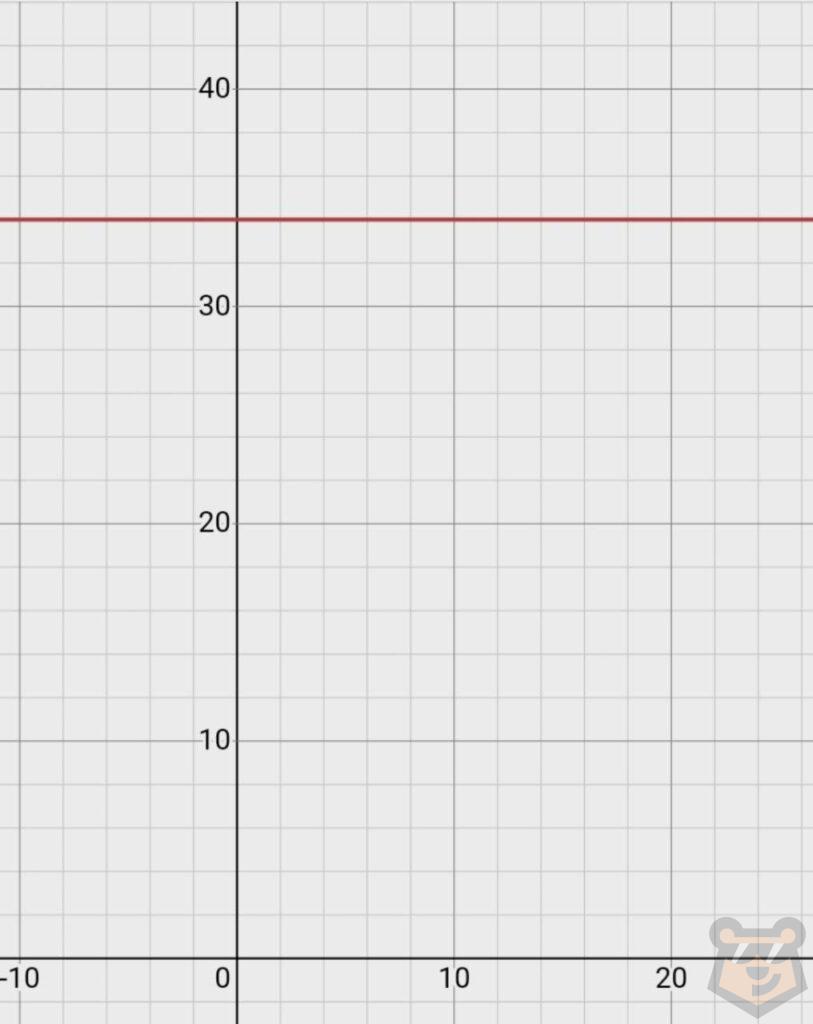
Теперь вычислим производную. Обратимся таблице №1, видим, что производная 34, как и любого другого числа равна нулю.
Значит скорость изменения функции тоже равна нулю. Убедиться в этом легко, ведь по графику мы видим, что никаких изменений у нас действительно нет.
2) Подберем функцию для второй недели у=34+2х. Делаем табличку и составляем график.
| х | 1 | 2 | 3 |
| у | 36 | 38 | 40 |
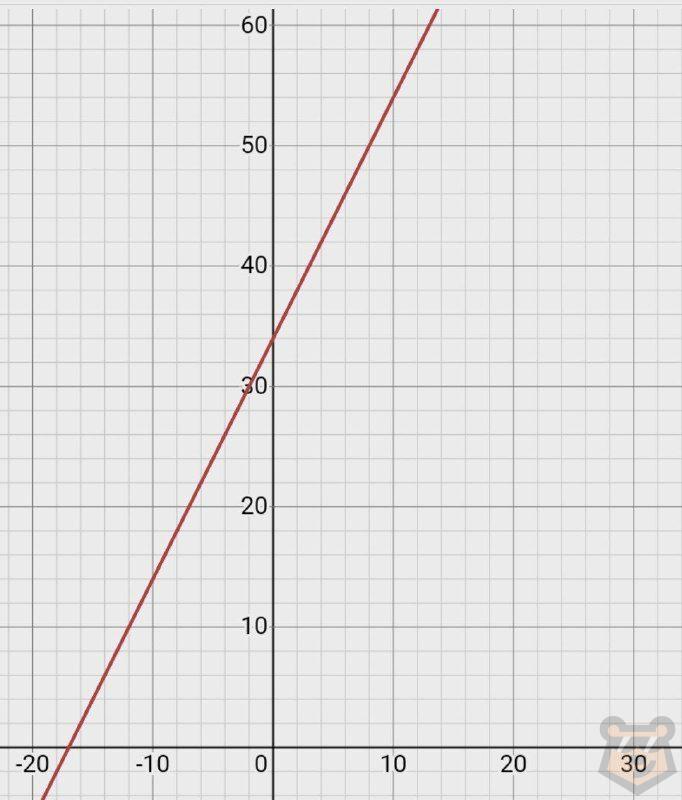
Сейчас ищем производную согласно правилам дифференцирования.
Выходит, что у’=34’+2х’. Вспоминаем, что 34’=0, тогда у’=2х’. Делаем вычисления.
у’=2×х’
у’=2×1
у’=2
Получается, что скорость изменения нашей функции (то есть прогресс ученика в чтении) является 2 слова в день. Это можно заметить и по самому графику, который растет.
Также можно искать несколько производных одной функции. Например, возможна и такая запись f(x)», или даже такая f(x)»’. Рассмотрим это на другом примере.
Нам дана функция f(x)=х^2. Необходимо найти третью производную.
Для начала ищем первую производную.
f(x)’=(х^2)’=2×х^(2-1)=2х
Затем беремся за второй шаг.
f(x)»=(2х)’=2×х’=2×1=2
И теперь мы можем найти третью производную.
f(x)»’=2’=0
И выходит, что f(x)»’=0.
Для того чтобы лучше запомнить это свойство производной и ее значение, обратимся к небольшой подсказке.
f(x) |  |
f(x)’ |  |
f(x)» |  |
Геометрический смысл производной
Геометрический смысл производной тесно связан с тригонометрией. Для того чтобы в этом убедиться и легче все понять, обратим внимание на один простой пример.
Дана функция у=х+2. Найдем ее производную, пользуясь нашими таблицами.
у’=х’+2’=1+0=1.
Запоминаем у’=1.
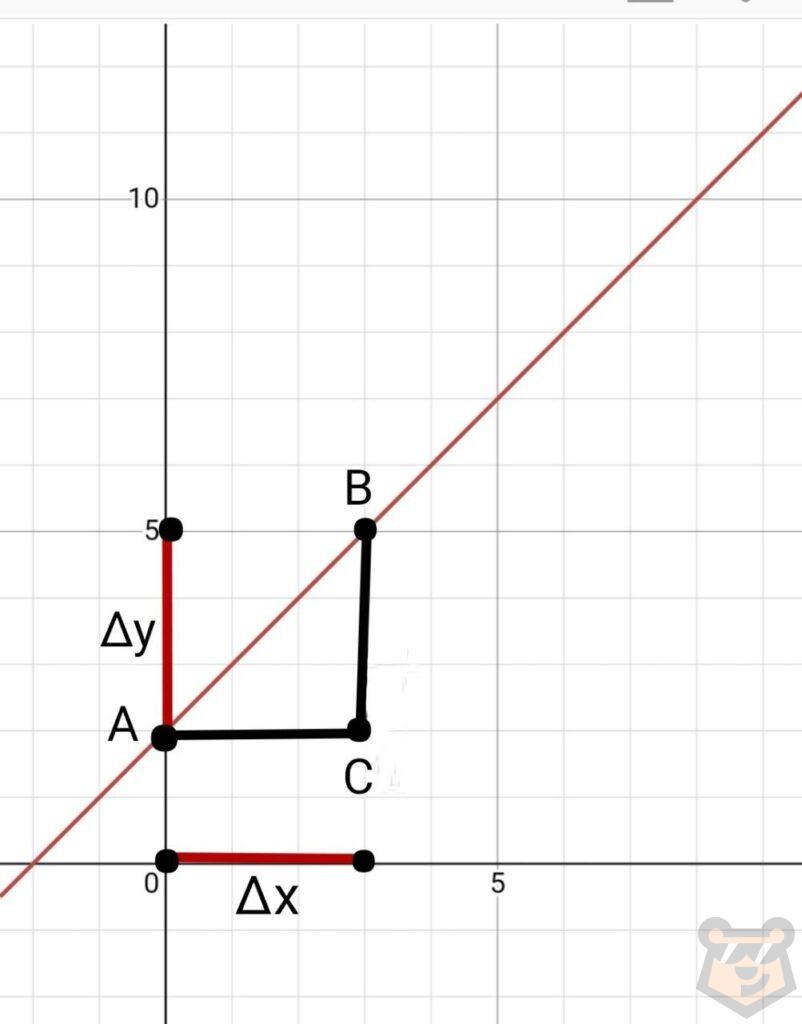
Теперь посмотрим на график нашей функции и выберем любую точку. Пусть это будет точка с координатами (3;5).
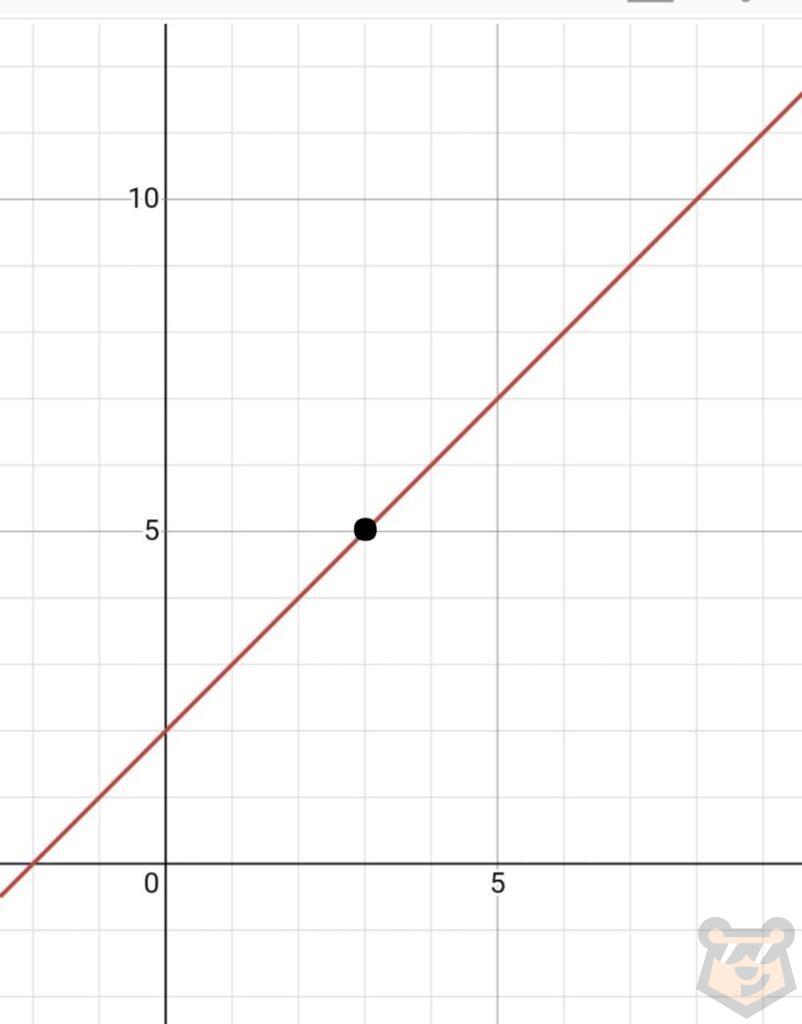
Начертим треугольник, который как бы «связал» и нашу точку, и нашу прямую. В итоге получим:
* В том случае, когда функция не будет линейной, то нужно просто провести касательную к нашей точке.
Назовем треугольник АВС. После отметим приращение функции и приращение аргумента. Простым языком выражаясь, приращение функции — это изменение переменной у, а приращение аргумента — это изменение переменной х. То есть получаем ∆у и ∆х.
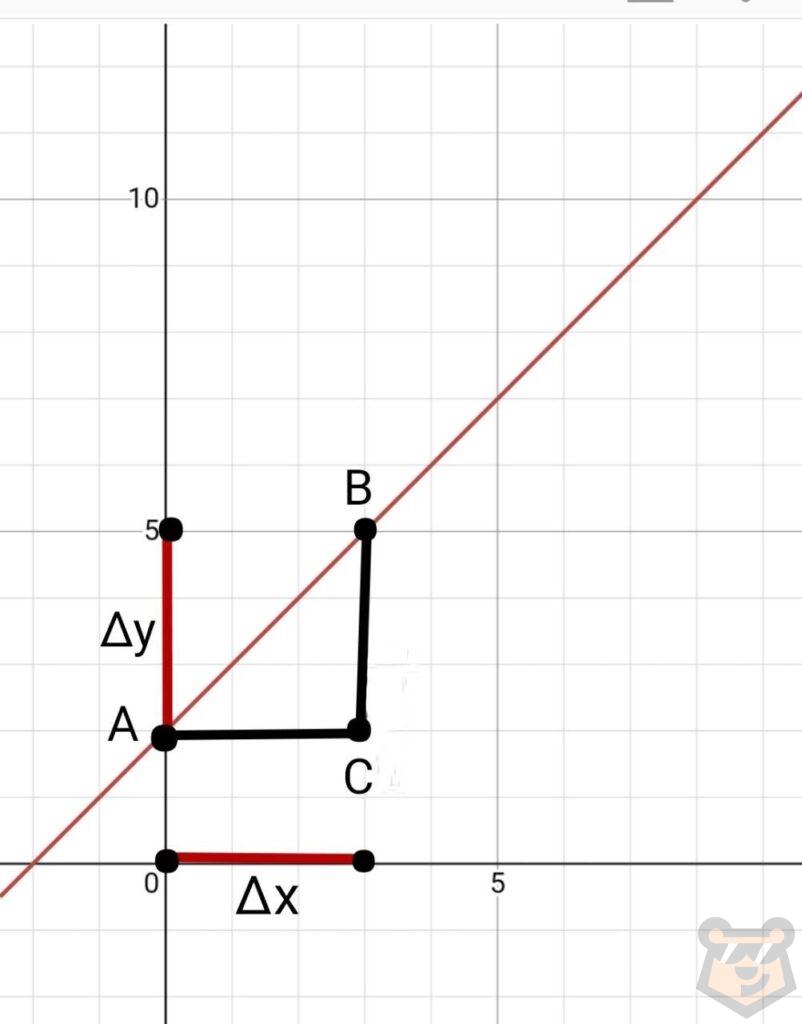
Отметив это на графике, замечаем, что ∆у=ВС, а ∆х=АС.
Из самого определения вспоминаем, что производная это отношение приращения функции к приращению аргумента. В формуле это имеет такой вид: ∆у/∆х.
Вспоминая равенство этих значений и сторон треугольника выходит: ∆у/∆х=ВС/АС.
Теперь переключаемся внимание на наш треугольник. Он у нас прямоугольный. И значит, что отношение ВС к АС, будет ни чем иным, как отношением противолежащего катета к прилежащему. И значит, что ВС/АС=tgА. Можно это представить и в более привычном виде: tgА=ВС/АС.
Подставляем найденное в выше полученное выражение: ∆у/∆х=tgА.
Найдем чему равен тангенс заданного угла. ВС=3, АС=3. tgА=3/3=1. Тогда ∆у/∆х=1. Значит производная равна 1. Данное значение сходится с тем, что мы получили при использовании формул.(1=1).
Делаем вывод:
Геометрический смысл производной заключается в том, что производной будет являться тангенс угла наклона касательной, проведенной к точке, которая принадлежит графику нашей функции.
Формула, отражающая это: f(x)’=tgА.
Физический смысл производной
Для того чтобы понять физический смысл производной обратимся к точке, которая движется по закону S=100t.
В данном случае в роли переменной у выступает S, а в роли переменной х — t. Значит, мы можем записать закон, по которому движется точка чуть по-другому: y=100x.
Вычислим производную. S’=(100t)’=100×t‘=100×1=100.
S’=100.
Составим таблицу и начертим график.
| t (х) | 1 | 2 | 3 | 4 |
| S (y) | 100 | 200 | 300 | 400 |
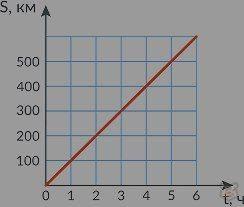
Сейчас посмотрим на наш график. Здесь отражен пройденный путь в зависимости от времени. Зная эти две величины мы можем найти третью — скорость.
Выберем точку на графике которая соответствует координатами (3;300).
Найдем мгновенную скорость по формуле V=S/t. V=300\3=100 км/ч.
Внимательно посмотрим на график и поймём, что S=∆y, a t=∆x.
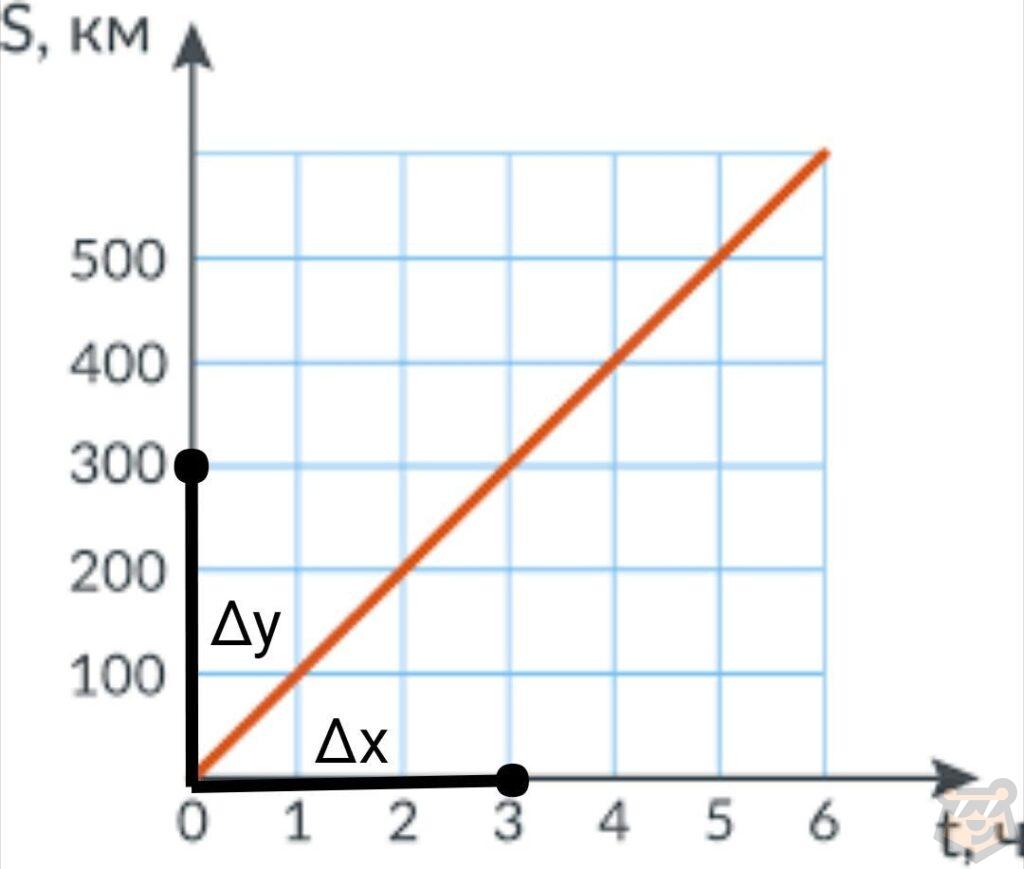
Выходит V=∆y/∆x. Значит скорость является производной пути, то есть S’=V.
Наши значения тоже сходятся. (100=100)
Делаем вывод:
Физический смысл производной заключается в том, что когда тело движется по закону S=S(t), то производная данного закона является мгновенной скоростью в момент времени t.
Формула, отражающая это: S’=V.
По тому же принципу установлено, что производная скорости является ускорением.
V’=a.
Это можно представить как вторую производную пути.
S»=a.
| S | путь | |
| S’ | V | скорость |
| S»=V’ | а | ускорение |
Физический смысл производной. | S’=V. S»=V’=а. |  |
Геометрический смысл производной. | f(x)’=tgА. |  |
Алгебраический смысл производной. | 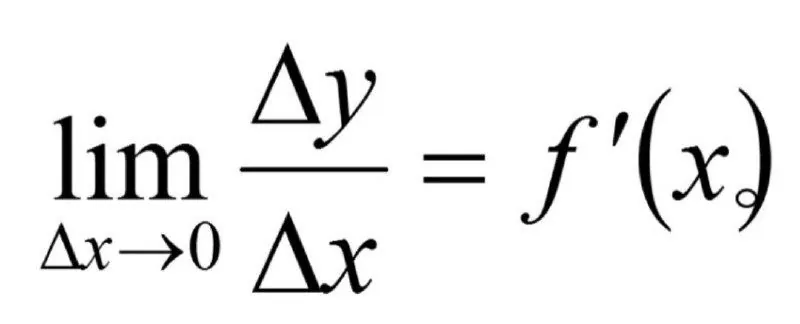 |  |
Уравнение касательной к графику функции.
Производные и уравнения касательных тесно связаны в геометрическом понимании функций.
Как мы говорили выше с точки зрения геометрии производная является тангенсом угла наклона касательной, проведенной к одной из точек нашей функции.
После вспоминаем, что tgA у нас характеризует угол наклона, а значит tgA будет являться коэффициентом k, о котором мы узнали, изучив разные виды функций и их графики.
И учитывая это, математики с легкостью смогли составить уравнение касательной к графику с использованием производной.
И выглядит оно следующим образом: y=f(x0)+f'(x0)×(x-x0), где
f(x) — функция, к которой мы ищем производную;
f'(x) — производная функции;
х0 — точка, через которую проходит наша касательная;
х — аргумент касательной, ее независимая переменная.
*На место х при нахождении уравнения касательной мы ничего не подставляем.
Пример№1. Найдите касательную к функции f(x)=3x^3+6x в точке х0=1.
1. Находим f(х0).
f(х0)=f(1)=3×(1^3)+6×1=3+6=9
2. a) Вычислим f'(x)
f'(x)=(3x^3+6x)’=(3x^3)’+(6x)’=(3×3x^2)+(6×1)=9x^2+6
b) Найдем f'(х0)
f'(х0)=f'(1)=9×(1^2)+6=9+6=15
3) Найдем х-х0.
х-х0=х-1.
4) Подставляем полученные выражения в наше уравнение.
у=9+15×(х-1).
Раскроем скобки, умножив их на 15.
у=9+(15×х)-(15×1)=9-15х-15=15х-6
И тогда уравнение касательной к нашей функции в точке х=1 будет таким: у=15х-6.
Производные сложных функций.
Бывает когда необходимо найти производную функций, которые не совпадают с табличными значениями. Например, у=sin(3х-4) или же у=√(4х-3).
Такие функции называют сложными. Можно заметить, что данные функции словно сложены из двух простых. Например, у=√(4х-3) состоит из у=√х и у=4х-3.
Получается, что √х является нашей внешней частью, а 4х-3 внутренней.
Обозначим нашу внешнюю функцию u, а внутреннюю v. Тогда наша формула будет выглядеть так: у’=u(v)’×v’.
Значит, производная сложной функции равна произведению производной внешней функции на производную внутренней.
Решим несколько задач.
Пример№1. Чему равна производная функции у=(4х+3)^4 ?
Вначале находим внешнюю и внутреннюю часть нашей функции.
u=х^4, v=4x+3.
1) Выходит: (х^4)’=4×(х)^3.
Вместо х подставляем 4x+3.
u(v)’=4×(4x+3)^3
2) v’=(4x+3)’=4
3) Тогда у’=((4х+3)^4)’=4×(4x+3)^3×4=16×(4x+3)^3.
Ответ: 16×(4x+3)^3.
Пример№2. Найдите производную сложной функции заданной уравнением у=sin(4x).
1) u=sinx
(sinx)’=cosx
u(v)’=cos(4x)
2) v=4x
v’=4x’=4
3) y’=cos(4x)×4=4cos(4x)
Ответ: 4cos(4x).
Практическая часть
Задание №1. Найдите производную функции у=13^х.
Решение. Это стандартное выражение, поэтому воспользуемся таблицей производных и сделаем вычисления. a^x=a^x×lna.
Получается у’=(13^х)’=13^x×ln13
Ответ: 13^x×ln13.
Задание №2. Чему равна производная функции, заданной уравнением у=3х+х^5-8х^2+3 ?
Решение. Используя таблицу №1 и правила дифференцирования, найдем производную.
у’=(3х+х^5-8х^2+3)’=(3х)’+(х^5)’-(8х^2)’+(3)’=3+5х^4-8×2х+0=3+5х^4-16х
Обычно принято записывать сперва переменные с х в наибольшей степени, после переменные с х в наименьшей степени, и только потом числа без х. Тогда у нас выйдет, что у’=5х^4-16х+3.
Ответ: 5х^4-16х+3.
Задание №3. Дана функция у=4соs(5x). Найдите ее производную.
Решение. Это сложная функция. Поэтому выделим вначале внешнюю и внутреннюю компоненты.
u=cosx
v=5x
Число 4 у нас выступает как константа. Поэтому согласно правилам дифференцирования мы можем сделать все вычисления и в конце просто полученное выражение умножить на 4.
(соsx)’=-sinx
Вместо х подставляем 5х. И выходит, что u'(v)=-sin(5x).
v’=(5x)’=5×x’=5×1=5
Теперь умножаем внешнюю функции на внутреннюю и на 4.
у’=4×(-sin(5x))×5=-20sin(5x)
Ответ: -20sin(5x).
Задание №4. Чему равняется производная функции, которая задана уравнение у=9х^2/9 ?
Решение. Воспользуемся данными из двух таблиц и найдем нужное нам значение.
(u/v)’=(u’×v — v’×u)/v^2.
у’=(2х^2/9)’=((2х^2)’×9 — 9’×2х^2)/9^2=(2х^2)’×9 — 9’×2х^2)/9^2=2×2х×9-0×2х^2/49=4х×9/49=4х/9
Ответ: 4х/9.
Задания по данному разделу, которые встречаются на ЕНТ
Задания по данной теме есть только в профильной математике. Предлагаю рассмотреть и решить типы задач, которые могут встретиться в тестировании.
Задание №1. Дана функция у=√(-3х^4-7х-6). Найдите ее производную.
Решение. Поэтому выделим вначале внешнюю и внутреннюю функцию.
u=√x
v=-3х^4-7х-6
1) (√x)’=1/2√х
На место х ставим -3х^4-7х-6.
u'(v)=1/2√(-3х^4-7х-6)
2) v’=(-3х^4-7х-6)’=(-3х^4)’-(7х)’-(6)’=(-3×4х^3)-(7×1)-0=-12х^3-7
Помним, что у’=u(v)’×v’. Значит у’=1/2√(-3х^4-7х-6)×(-12х^3-7)=-12х^3-7/2√(-3х^4-7х-6).
Ответ: -12х^3-7/2√(-3х^4-7х-6).
Задание №2. Тело движется по закону S(t)=14t^2+3t-10. Найдите какой скоростью будет обладать тело на 3 секунде движения.
Решение. Применяем физический смысл производной — S’=V.
S(t)’=V(t)=(14t^2+3t-10)’=(14t^2)’+(3t)’-(10)’=(2×14x)+(3×1)-0=28t+3.
V(t)=28t+3
Вычисляем V(3).
V(3)=28×3+3=84+3=87.
Ответ: 87.
Задание №3. Точка движется по закону S(t)=t^3-2.5t^2+2t. Определение через сколько секунд скорость тела станет равна нулю.
Решение. Вновь воспользуемся тем, что физический смысл производной заключается в том, что S’=V.
S(t)’=V(t)=(t^3-2.5t^2+2t)’=(t^3)’-(2.5t^2)’+(2t)=(3×t^2)-(2×2.5t)+(2×1)=3t^2-5t+2
V(t)=3t^2-5t+2.
Приравниваем нашу скорость к нулю. V(t)=0, выходит, что 3t^2-5t+2=0.
Решаем данное уравнение.
D=(-5)^2-(4×2×3)=25-24=1=1^2
x1=5+1/2×3=6/6=1.
x2=5-1/2×3=4/6=2/3.
Ответ: 2/3, 1.
Задание №4. Найдите производную функции у=³√(5х^4-6х).
Решение. Это сложная, поэтому выделяем наши u и v.
u=³√х
v=5х^4-6х
Понимаем, что в таблице производных нет выражение по типу ³√х, поэтому представим корень третей степени, в виде степени 1/3. То есть ³√х=х^(1/3). Вот теперь мы можем делать вычисления, ведь знаем как находить производную х в какой-то степени: х^n=n×x^(n-1).
1) (х^(1/3))’=1/3×х^(1/3-1)=1/3×х^(1/3-3/3)=1/3×х^(-2/3).
Преобразуем х^(-2/3) в ³√(х^(-2)).
Получим ³√(1/х^2)=1/³√х^2.
Вместо х подставим 5х^4-6х.
u'(v)=1/³√(5х^4-6х)^2.
2) v’=(5х^4-6х)’=(5х^4)’-(6х)’=(4×5x^3)-(6×1)=20x^3-6
3) y’=1/³√(5х^4-6х)^2×(20x^3-6)=20x^3-6/³√(5х^4-6х)^2
Ответ: 20x^3-6/³√(5х^4-6х)^2.
Задание №5. Найдите точки, принадлежащую касательной, проведенной к графику функции у=х^2+6х-2 в точке х0=2.
А) (1;4)
B) (3;20)
C) (5;43)
D) (2;14)
Решение. Сперва мы найдем уравнение нашей касательной, а затем будем вместо нашего аргумента подставляем х из данных точек. И те значения функции, которые совпадут с у этих точек, и будут являться решением задачи.
1. f(x0)
f(x0)=f(2)=(2^2)+(6×2)-2=4+12-2=14
2. f'(x0)
a) f'(x)=(х^2+6х-2)’=(х^2)’+(6х)’-(2)’=(2×2)+)6×1)-0=2x+6
b) f'(x0)=f'(2)=2×2+6=4+6=10
3) х-х0
х-х0=х-2
4) у=14+10×(х-2)=14+10×х-10×2=14+10х-20=10×-6
у=10х-6
5) Подставляем х, находим у и сравниваем.
А) (1;4) х=1 у=4
у(1)=10×1-6=10-6=4
4=4
Точка принадлежит касательной.
B) (3;20) х=3 у=20
у(3)=10×3-6=30-6=24
20≠24
Точка не подходит.
C) (5;43) х=5 у=43
у(5)=10×5-6=50-6=44
43≠44
Точка не принадлежит касательной.
D) (2;14) х=2 у=14
у(2)=10×2-6=20-6=14
14=14
Точка подходит.
Ответ: А, D.
Задания для самопроверки:
Задание№1.
Чему равна производная функции у=10х^3-х^2+√х ?
Задание№2.
Найдите производную функции, заданной уравнение у=15sin(3x-2).
Задание№3.
Чему будет равно ускорение тела через 1 секунду, если оно движется по закону S(t)=0.5t^8-2t+t ?
Ответы: 1 — 30х^2-2х+1/2√х., 2 — 45cos(3x-2), 3 — 24.
