Пределы
Предел — это еще одно явление, которое очень тесно связано с математическим анализом. И прежде чем с ним познакомиться необходимо изучить что такое функция. Ведь пределы определяют поведение функции в различных точках, помогая нам анализировать ее свойства. Например, предел в определенной точке может определить ее непрерывность или существование асимптот. Пределы функций также используются для нахождения значений функций в бесконечно удаленных точках. В общем, понимание пределов функций существенно для математиков, и применяется в различных областях, начиная от физики и экономики до информационных технологий и строительства.
Предел —
это такое число, к которому будет приближаться значение(у) нашей функции при стремлении аргумента (х) к одному строго определенному числовому значению.
Мы помним, что переменная у зависит от переменной х согласно данному нам закону f(x). То есть мы подставляем х в наш закон и получаем у.
Для того, чтобы легче уловить суть, предлагаю немного по-другому посмотреть на само определение функции и разобрать вместе с нами несколько примеров. Давайте посмотрим на иллюстрации и проведем аналогии.
| х | f(x) | у |
 |  |  |
Выходит:
х — наш стартовый набор.
f(x) — завод, «перерабатывающий» стартовый набор
у — наш конечный результат после переработки.
Сейчас решим пару заданий согласно нашей шпаргалке.
Пример №1. Дана функция f(x)=3x. Пусть х=3.
Стартовый набор — 3
Завод- 3×3
Результат — 9
Пример №2. Функция задана f(x)=x^3. Наш х=2.
Стартовый набор — 2
Завод- 2^3
Результат — 8
Пример №3. Есть функция у=х+3.
Теперь рассмотрим пример, когда наш аргумент будет на какую-то малейшую долю приближаться к значению 4.
Получается:
х1=3.8
х2=3.86
х3=3.9
х4=3.94
х5=3.99
Сделаем небольшую таблицу для наглядности и удобства.
| х | f(x) | у |
| 3.8 | 3.8 + 3 | 6.8 |
| 3.86 | 3.86 + 3 | 6.86 |
| 3.9 | 3.9 + 3 | 6.9 |
| 3.94 | 3.94 + 3 | 6.94 |
| 3.99 | 3.99 + 3 | 6.99 |
Смотря на наши числовые данные понимаем, что наш конечный результат будет с каждым разом становиться все ближе и ближе к отметке «7». Однако наш у никогда её не то, что перешагнуть, он даже ее достигнуть не сможет.
Таким образом, «7» это строго очерченная граница конкретно для данного случая. Это и будет являться нашим пределом. Такие пределы существуют и для других ситуаций.
Очередной пример. Нам известно, что для приготовления 5 тортов необходимо 50 яиц.
Делаем вывод, что из 47, 48 и даже из 49 яиц мы никак не сделаем 5 полноценных тортов. Такая же схема и при работе с пределами.
Теперь предлагаю узнать как мы на письме отмечаем пределы и все, что с ними связано.
Сам пределом обозначается следующим образом: lim
А стремление аргумента к какому-то числу мы записываем так: x→x0
И понимаем, что запись предела функции у=4х^2-3, аргумент которой стремиться к -1 будет обозначаться, как на иллюстрации.
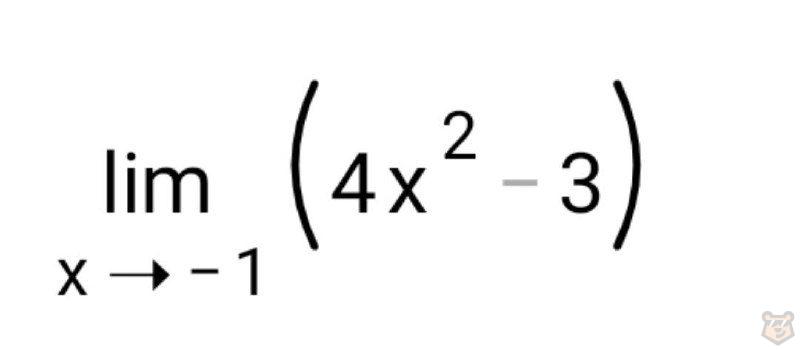
Практическая часть.
Для закрепления теоретического материала перейдем к практической части и выполним несколько задач.
Для того, что найти вышеприведенный предел мы просто в нашу функцию вместо х подставим -1 и вычислим у.
у=4×1^2-3=4-3=1
Ответ: 1.
Казалось бы все легко и быстро, но иногда бывают ситуации, когда нам для начала необходимо сделать кое-какие преобразования в данной нам функции и только потом подставлять то число, к которому стремиться х.
Почему так происходит? Предлагаю в этом разобраться на примере одного простого (правда только на первый взгляд) задания.
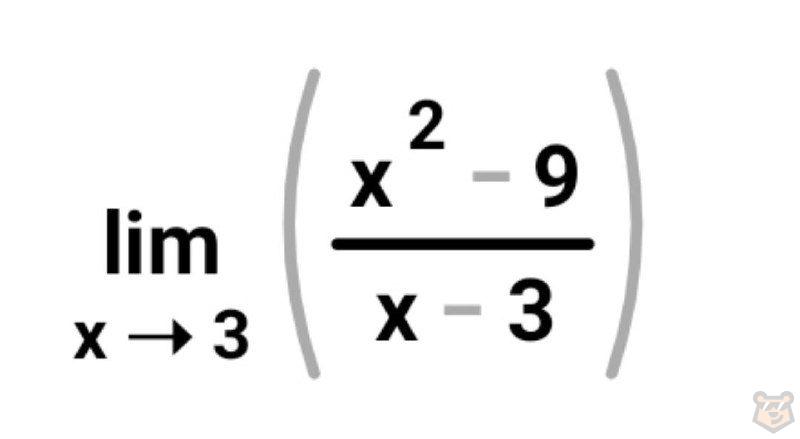
Подставляем 3 в каждую часть нашей дроби.
Числитель: х^2-9=3^2-9=9-9=0
Знаменатель: х-3=3-3=0
У нас вышло 0/0. А такое выражение является неопределенностью, простым языком, если ноль разделить на ноль, то мы можем получить абсолютно любое число. Поэтому нам необходимо преобразовать нашу функцию.
Если внимательно посмотреть на наш числитель х^2-9, то легко заметить, что его можно разложить на множители по формулам сокращенного умножения.
И тогда получаем, что х^2-9=(х-3)(х+3).
Подставляем полученное выражение в нашу дробь.
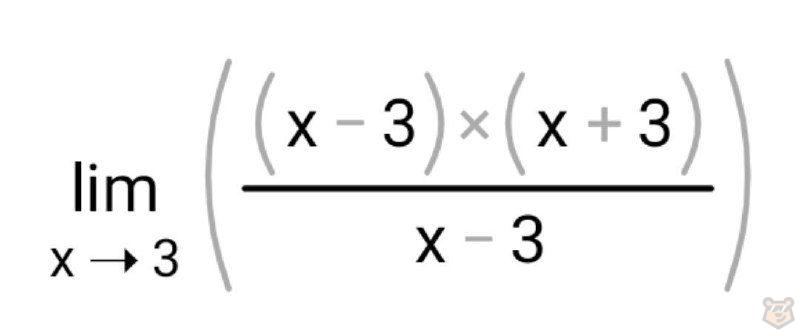
Сокращаем (х-3) и в знаменатели, и в числителе.
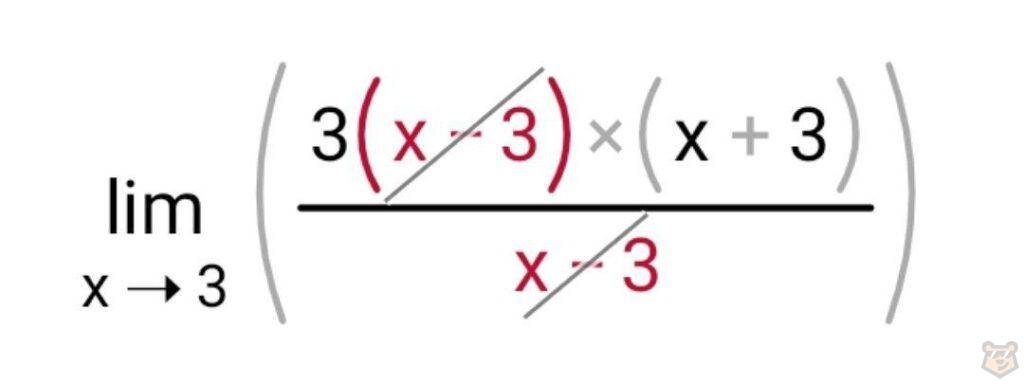
Тогда у нас остается:
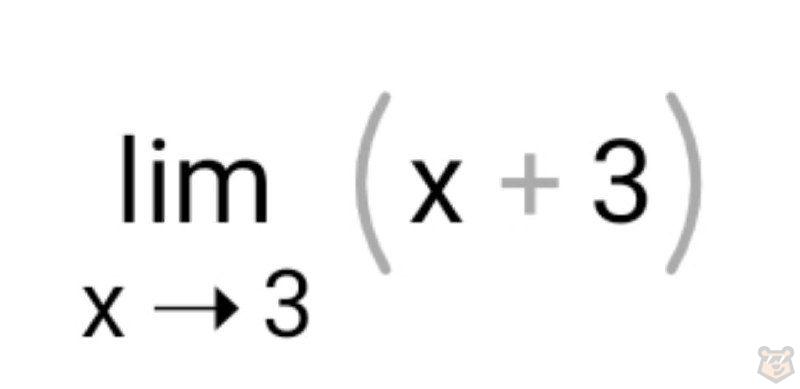
И теперь мы можем найти наш предел.
Ставим на место х 3, и вычисляем.
х+3=3+3=6
Ответ: 6.
Обратив внимание на пример №2. Он будет чуть сложнее.
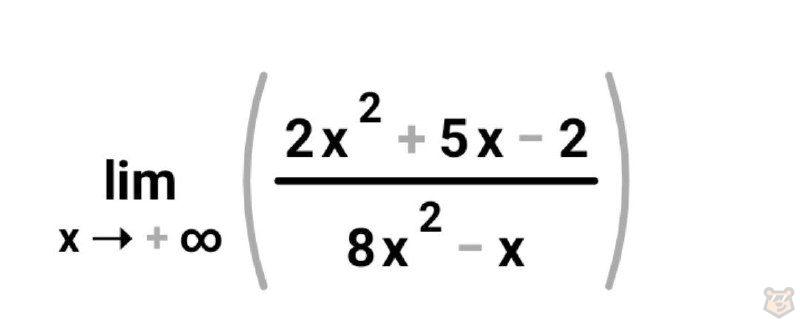
Наш х стремится к плюс бесконечности. Давайте вновь подставим в наши дроби то, к чему приближается наш аргумент.
В числителе у нас получится +∞, и в знаменателе тоже выйдет +∞.
Подставим полученные значения в дробь. Выходит +∞/+∞. Такое выражение тоже является неопределенностью. Поэтому мы должны опять «трансформировать» нашу функцию.
В данном случаем мы должны и числитель и знаменатель разделить на переменную в старшей степени, то есть в самой большой степени. У нас это будет х^2. Получим:
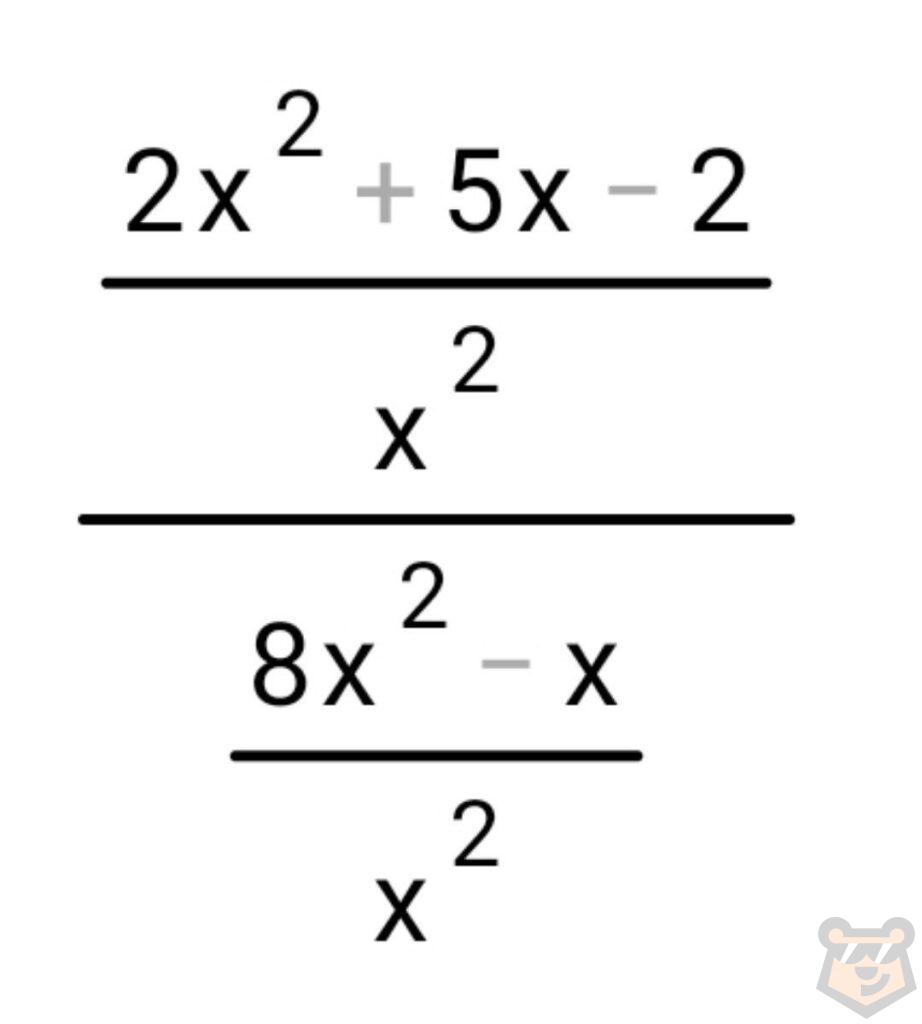
Теперь разделим каждый член числителя на х^2. Выйдет следующее.
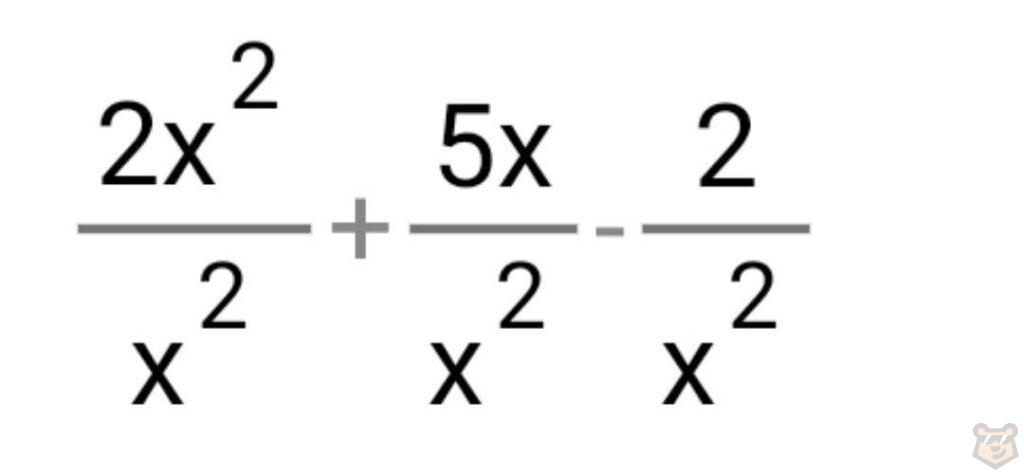
Сокращаем и получаем.
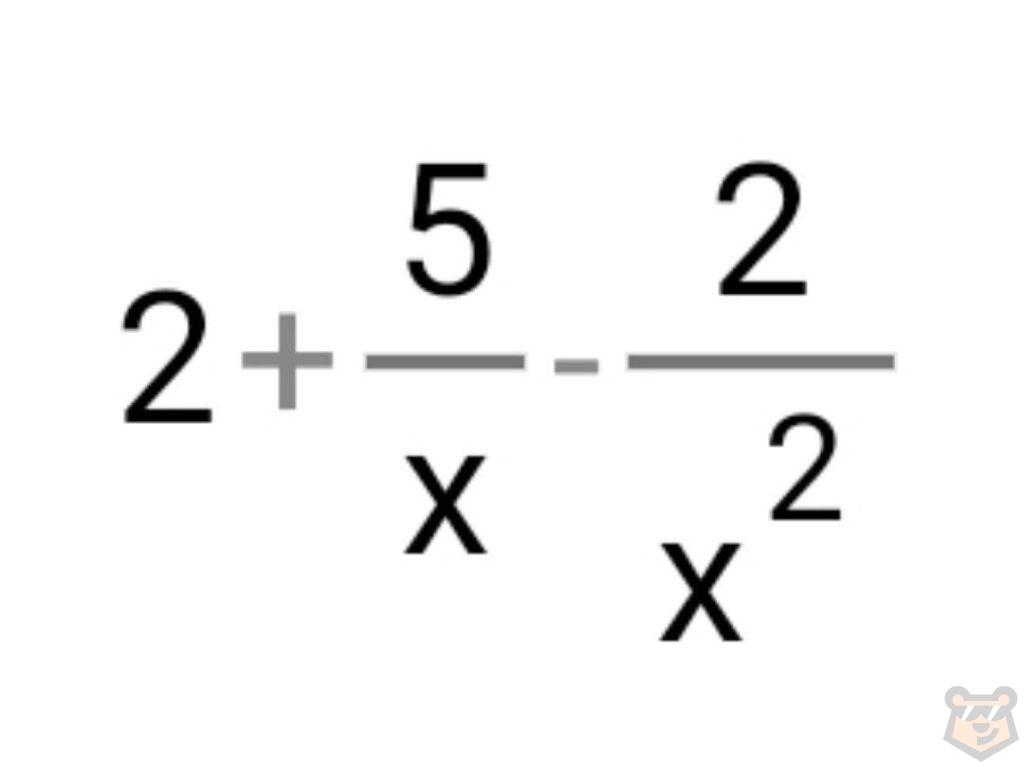
Наши дроби, в знаменателе которых находится наш, стремящийся к плюс бесконечности, будут равны нулям.
Числитель: 2+0-0=2.
То же самое проделываем со знаменателем. Делим каждый член на х^2. Получаем:
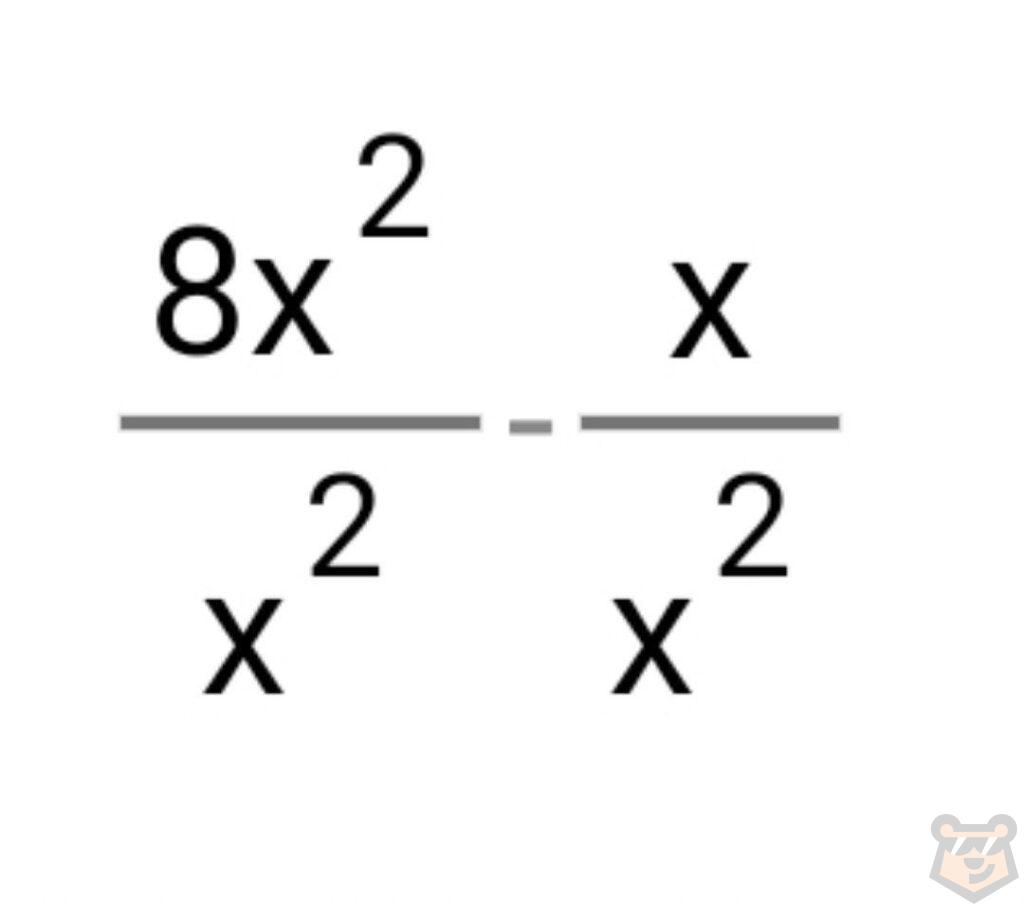
Сокращаем и вычисляем.
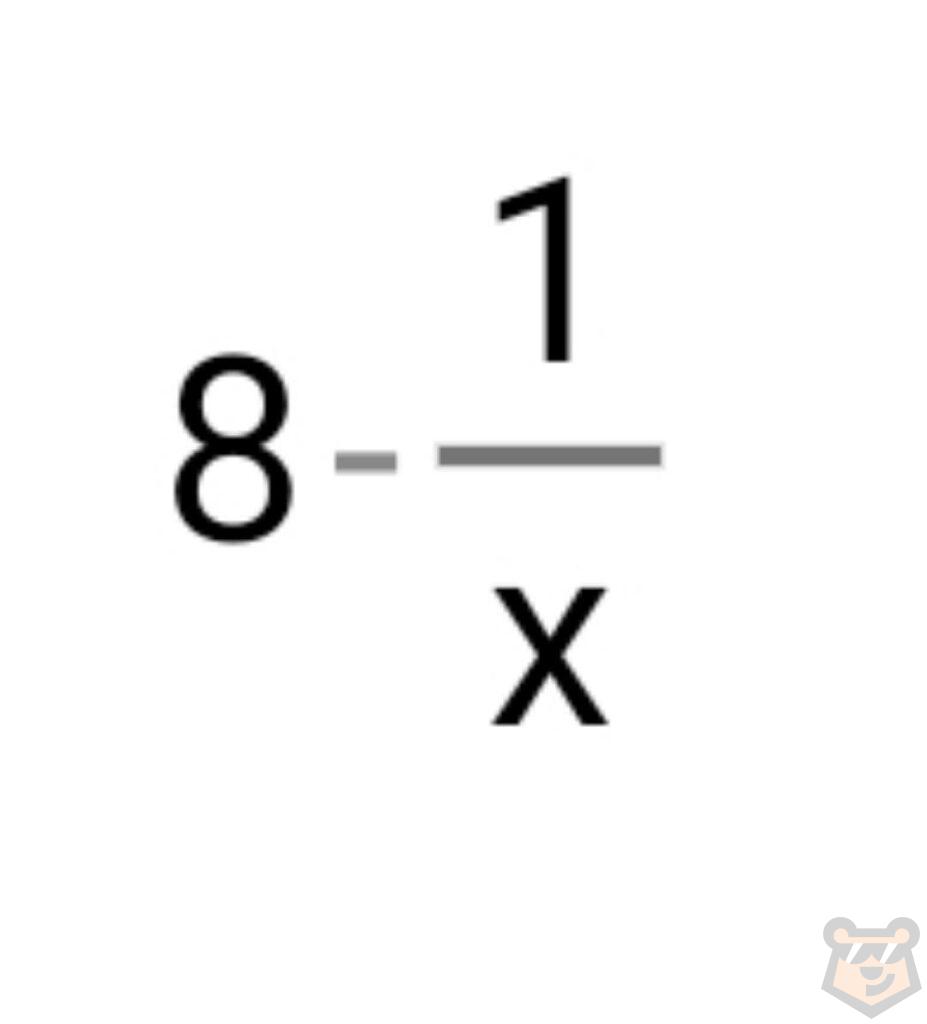
Вспоминаем про дроби с бесконечностей в знаменателе и получаем 8-0=8.
И при таком раскладе у нас выходит:
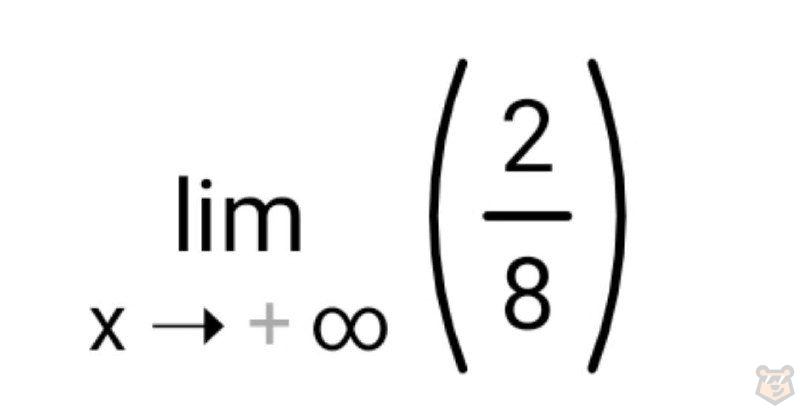
х нет, подставлять нечего. Значит пределом будет дробь 2/8. Сократим ее и вычислим 1/4.
Ответ: 1/4.
Для того, чтобы запомнить как решать задачи с каждой из неопределенностей, обратимся к подсказке-мему:
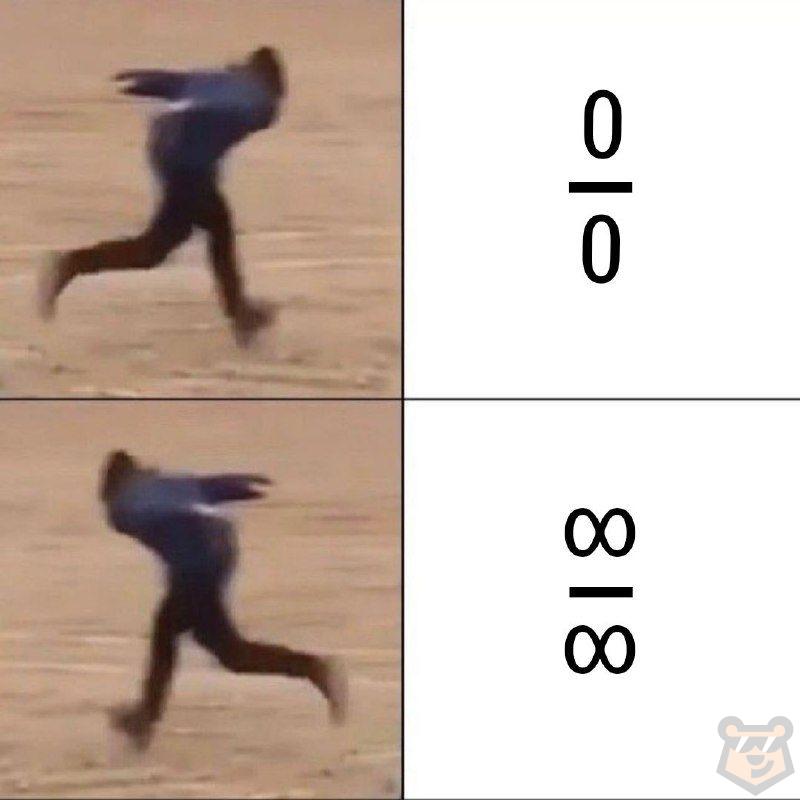
Задания по данному разделу, которые встречаются на ЕНТ.
Пределы функции на тестировании встречаются только в профильной математике.
Давайте посмотрим какие типы задач по данной теме вам могут попасться.
Задание №1.
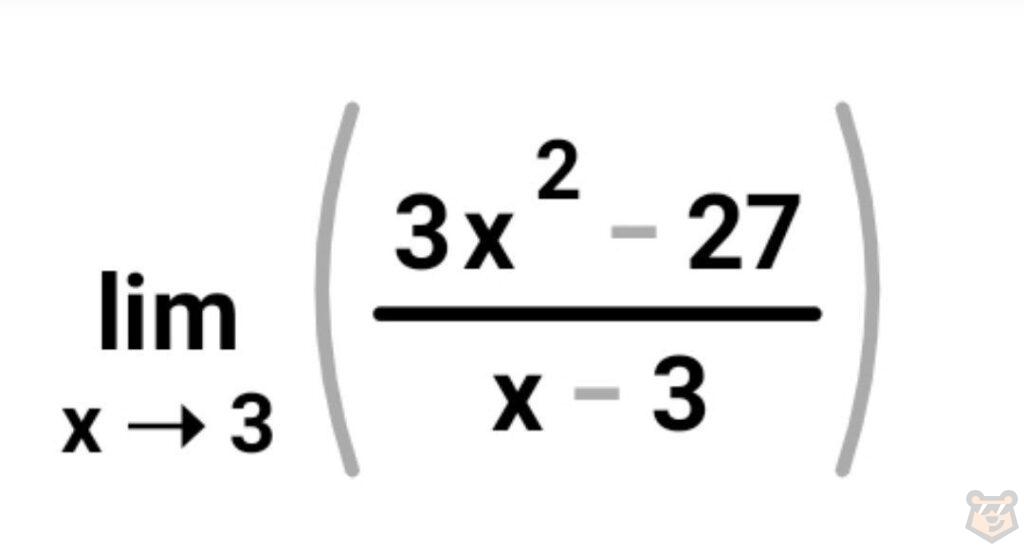
Решение. Подставляем 3 в наш числитель и знаменатель.
Числитель: 3×х^2-27=3×3^2-27=27-27=0
Знаменатель: х-3=3-3=0
У нас вышло 0/0. Значит нужно преобразовать функцию.
Если тщательно всмотреться в наш числитель 3×х^2-27, то нетрудно заметить, что мы можем вынести общий множитель 3 за скобку.
И тогда получаем.
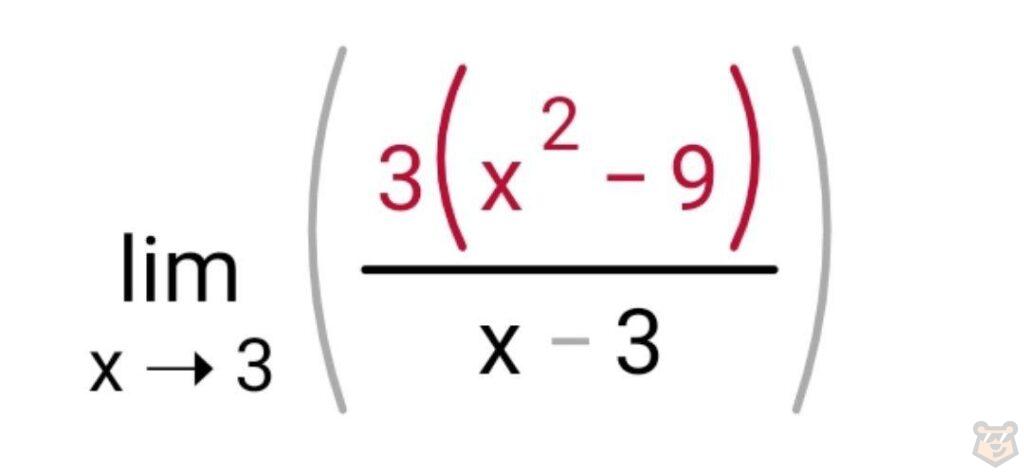
Вновь обращаем внимание на числитель и замечаем, что (х^2-9) можем разложить согласно формулам сокращенного умножения. Выходит:
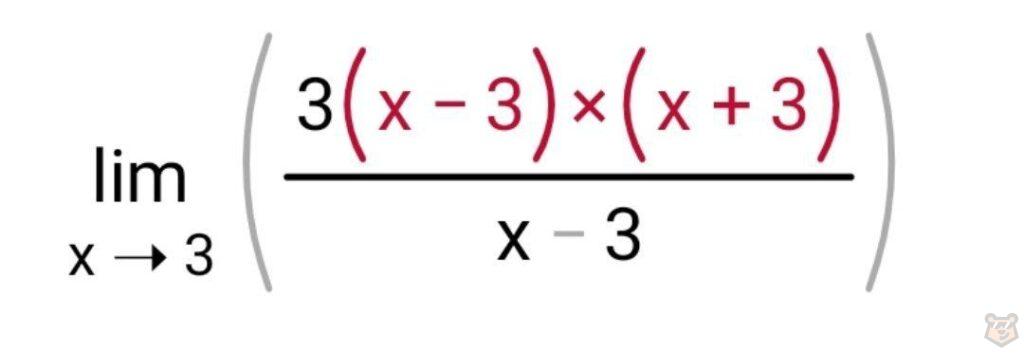
Теперь сокращаем (х-3) и в знаменатели, и в числителе.
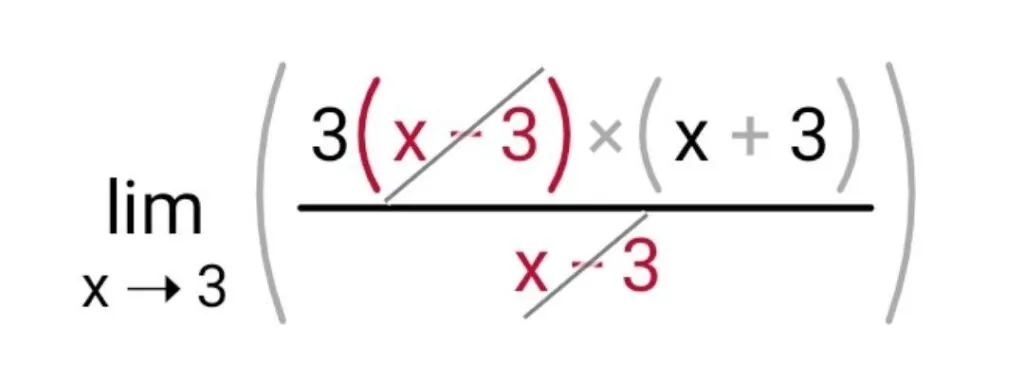
Тогда у нас остается:
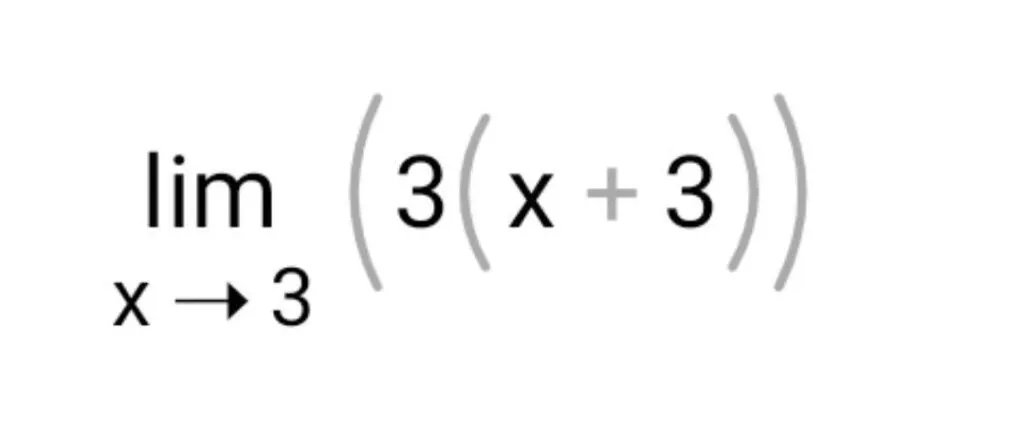
Умножаем 3 на скобку и вычисляем:
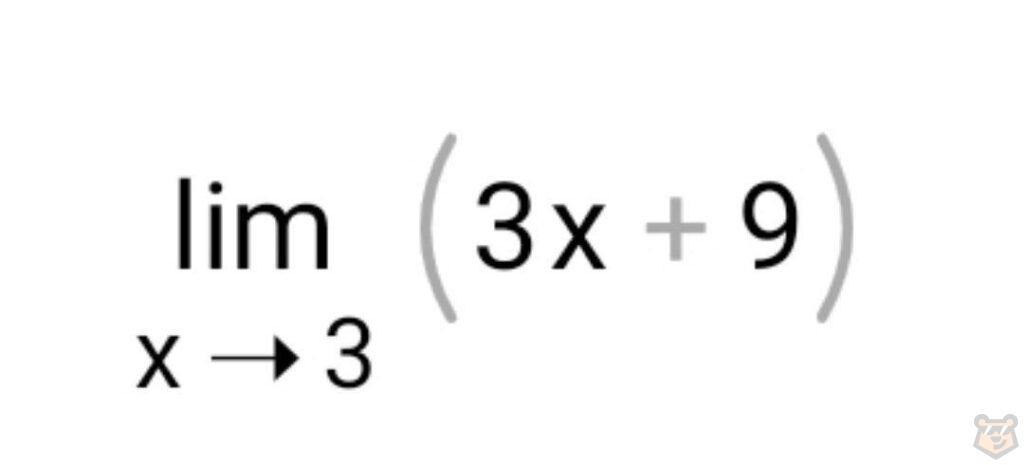
И сейчас мы в силах найти наш предел.
3х+9=3×3+9=9+9=18
Ответ: 18.
Задание №2.
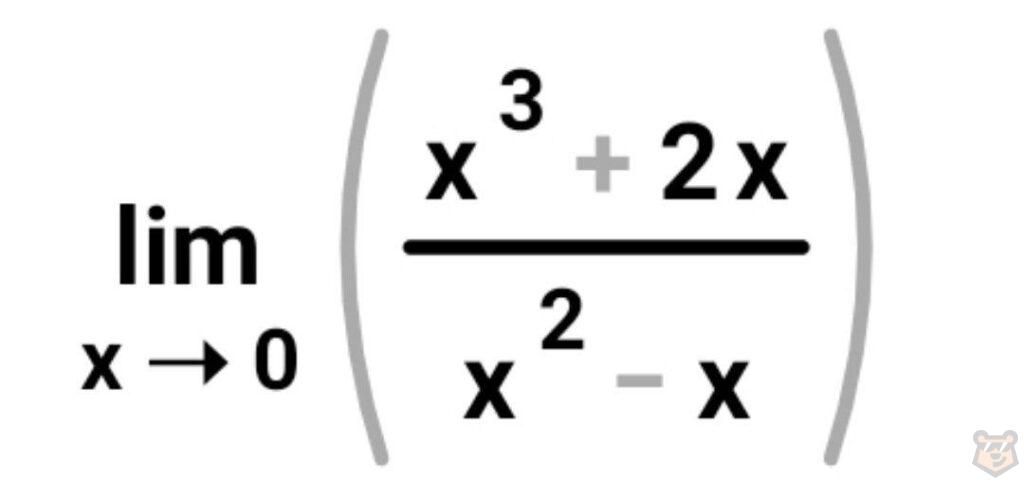
Подставляем 0 в нашу дробь
Числитель: 0^3+2×0=0+0=0
Знаменатель: 0^2-0=0-0=0
У нас опять выходит 0/0. Значит нужно «трансформировать» функцию.
Внимательно смотрим на наш знаменатель х^3+2х и отмечаем, что мы можем вынести общий множитель х за скобку. И тогда получаем:
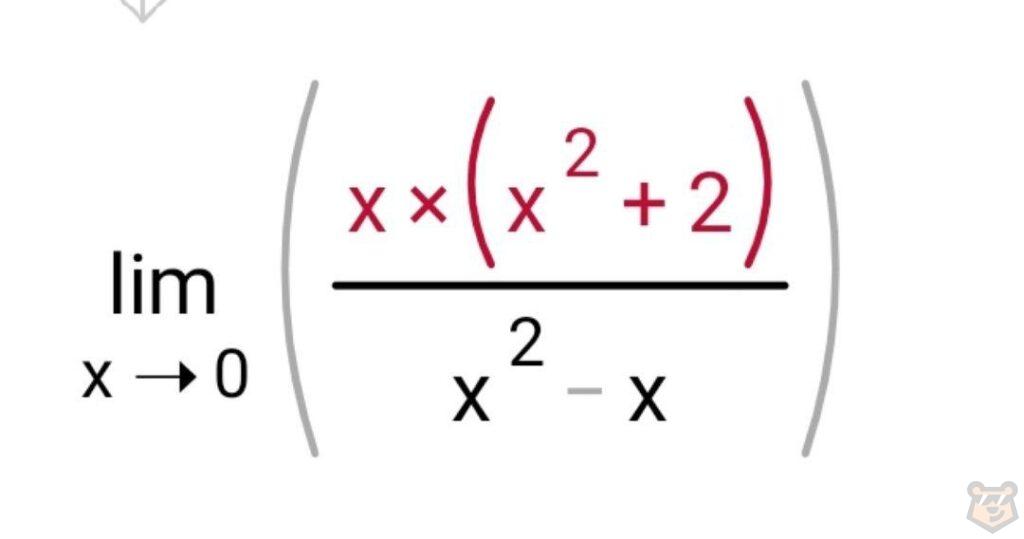
Теперь обращаем внимание на знаменатель х^2-х и замечаем, что в силах вынести общий множитель х за скобку. Выходит следующее:
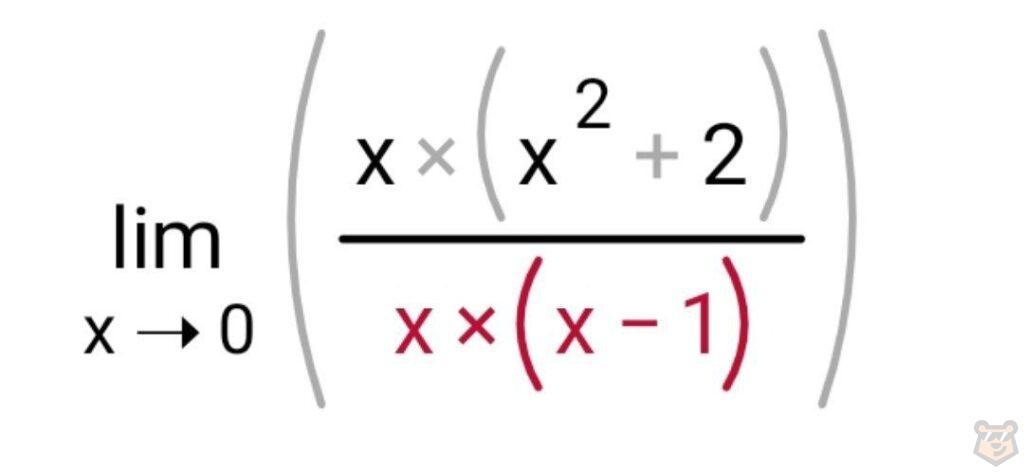
Теперь сокращаем х и в знаменатели, и в числителе.
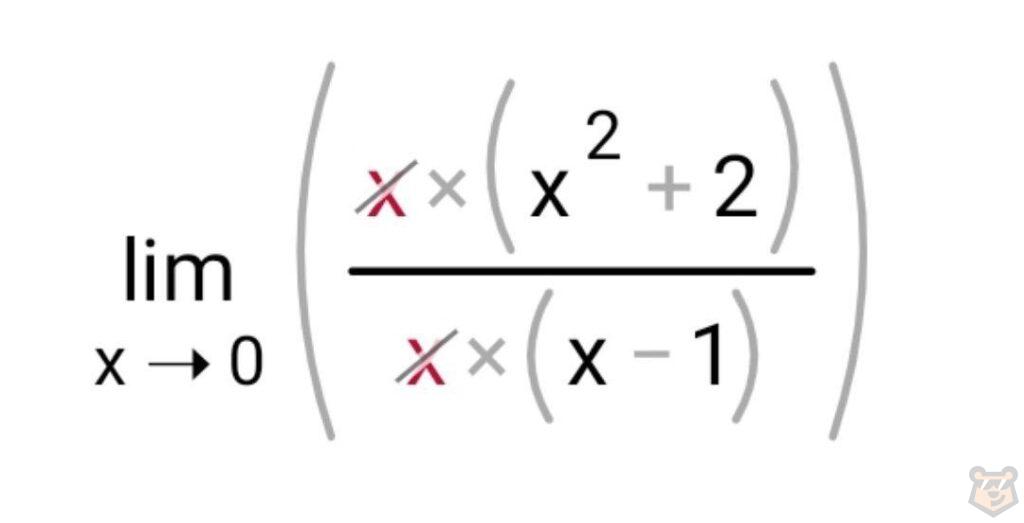
Таким образом у нас остается:
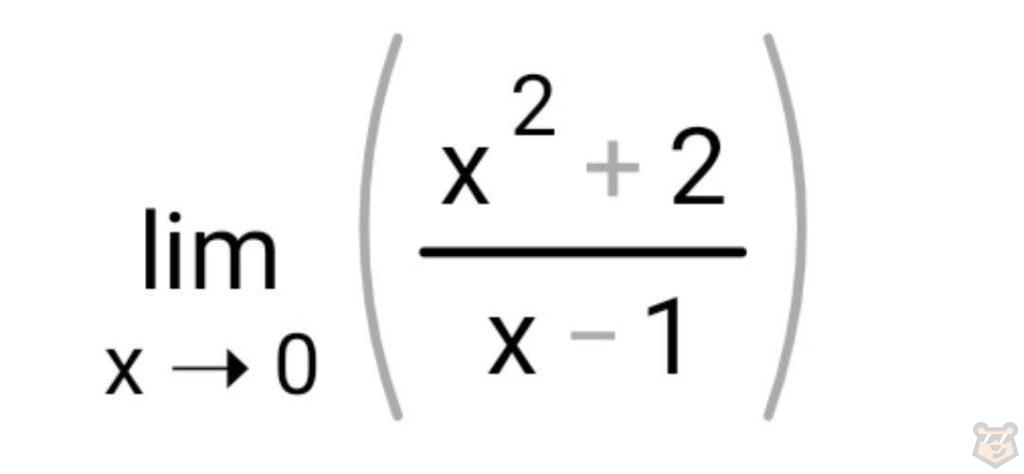
И теперь мы можем вычислить наш предел.
0^2+2/(0-1)=2/-1=-2
Ответ: -2.
Задание №3.
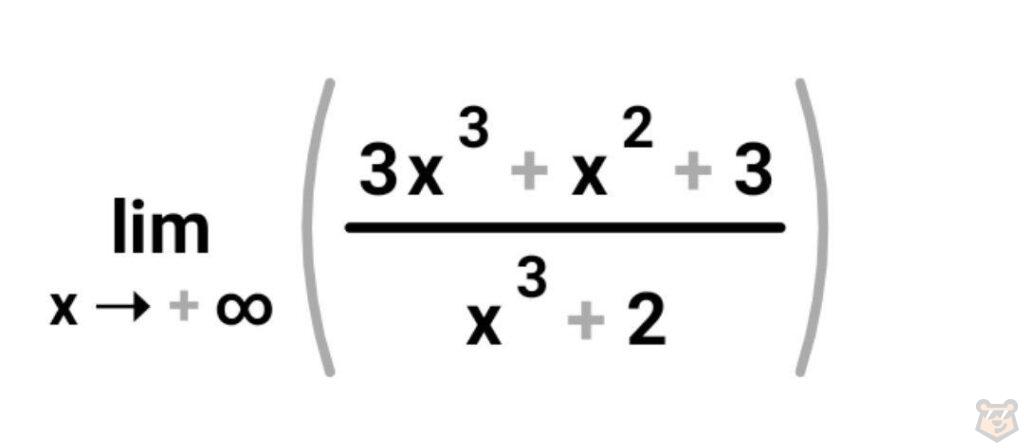
При таком раскладе у нас х стремится к бесконечности.
Подставляя её в нашу дробь выходит ∞/∞. Решаем задание по выведенному выше алгоритму. Делим каждый член числителя на переменную в старшей степени х^3. Получаем:
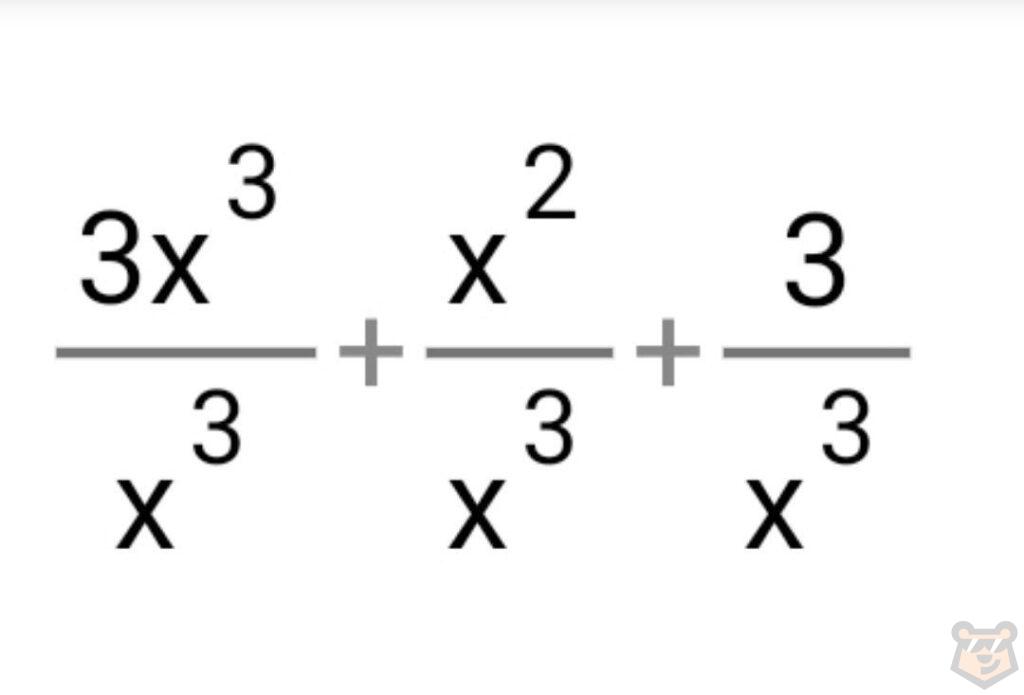
Теперь сократим:
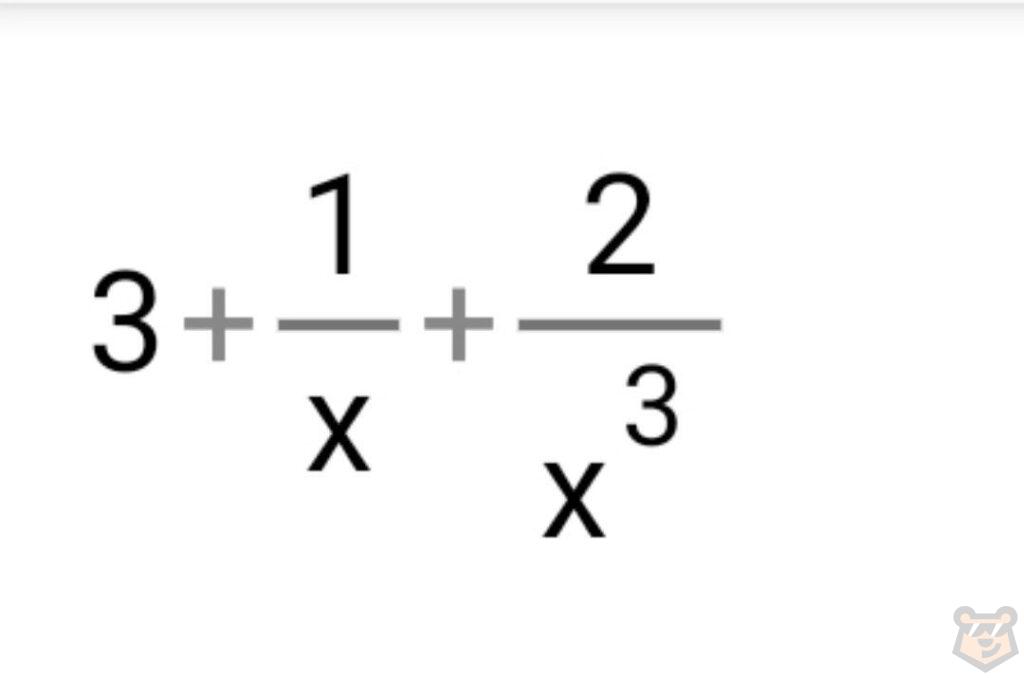
Помним, что дроби с нашим х превращаются в нуль. Значит числитель будет равен 3+0+0=3.
Повторяем тоже самое со знаменателем.
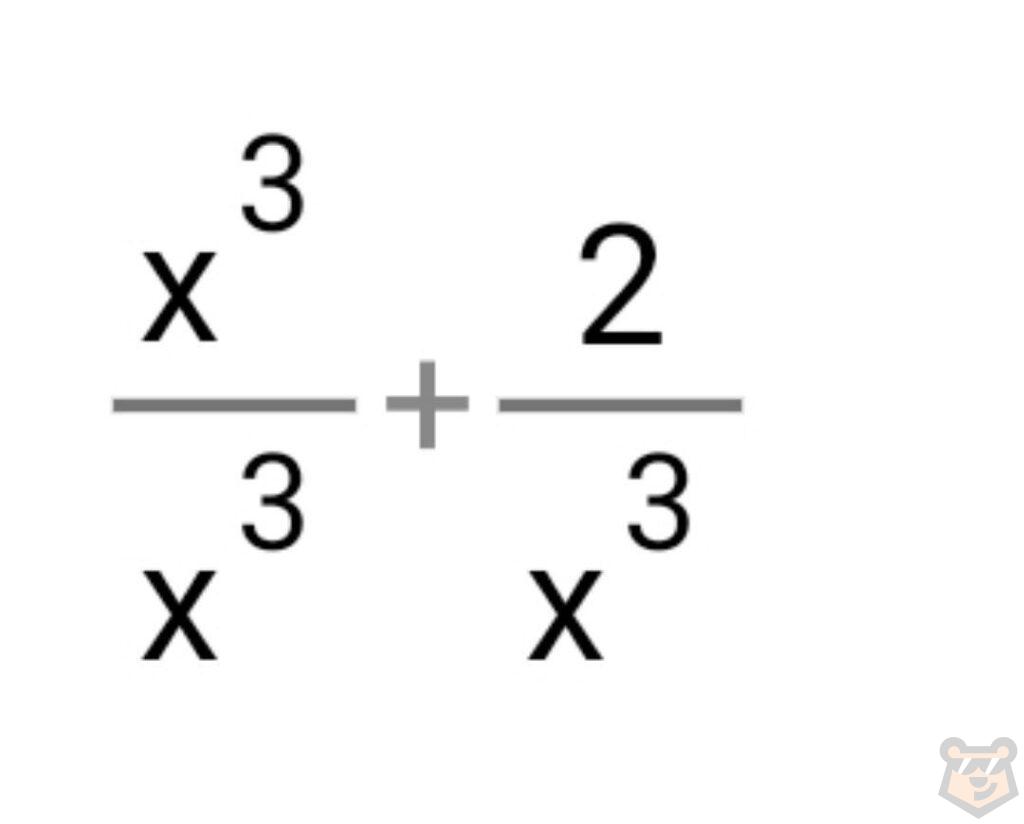
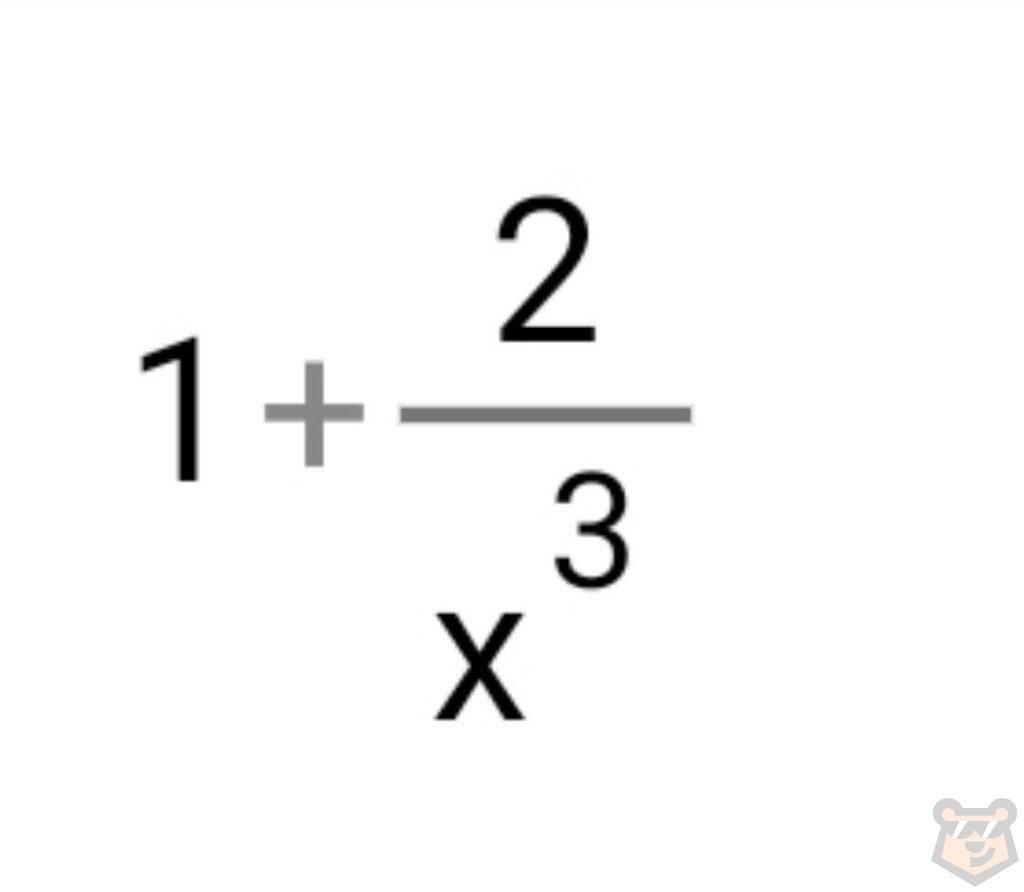
Знаменатель равен 1+0=1
Подставляем в нашу дробь и выходит.
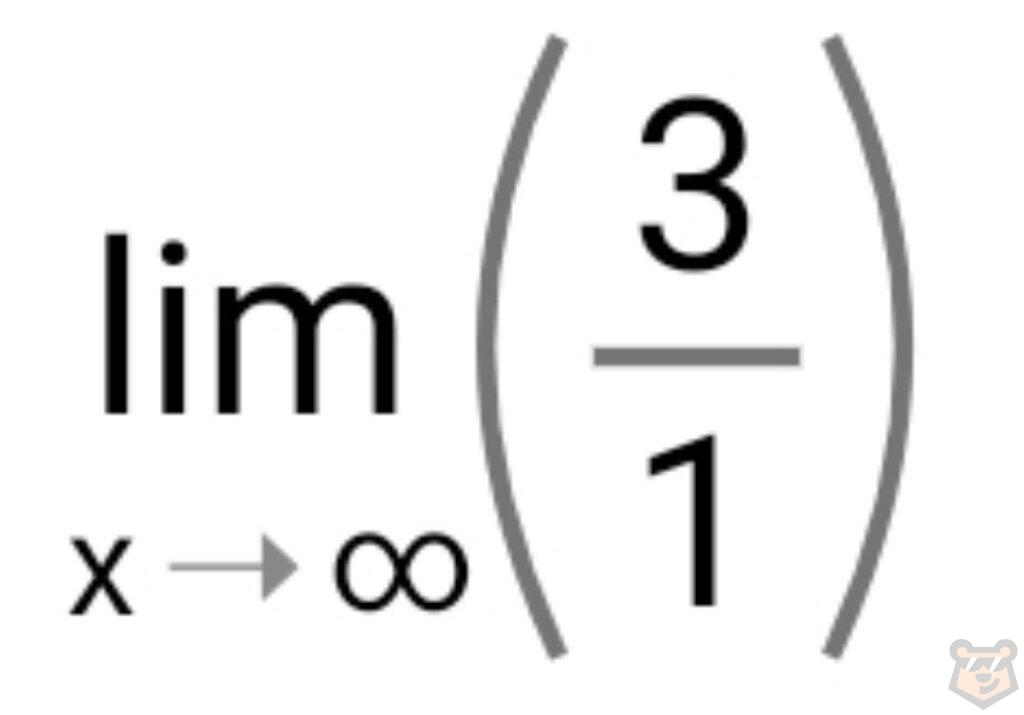
И видим, что нашим пределом будет дробь 3/1. То есть 3.
Ответ: 3.
Задания для самопроверки:
Задание №1.
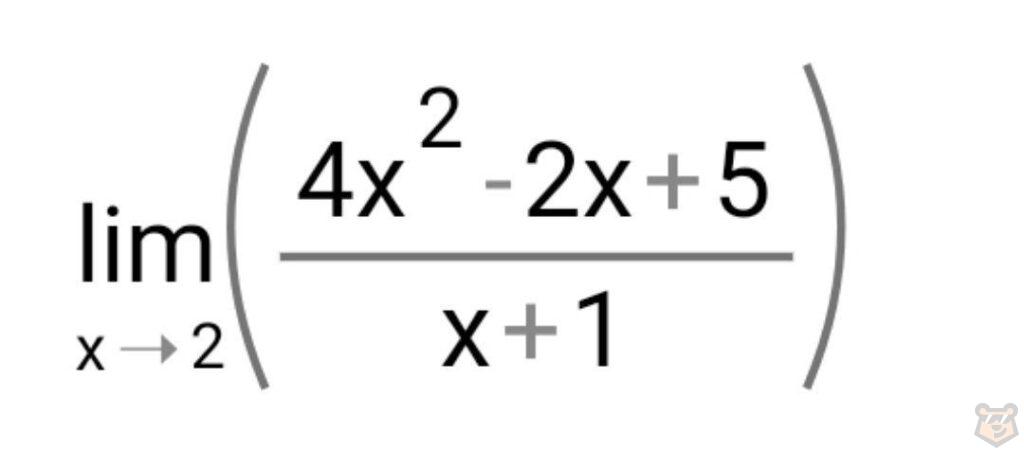
Задание №2.
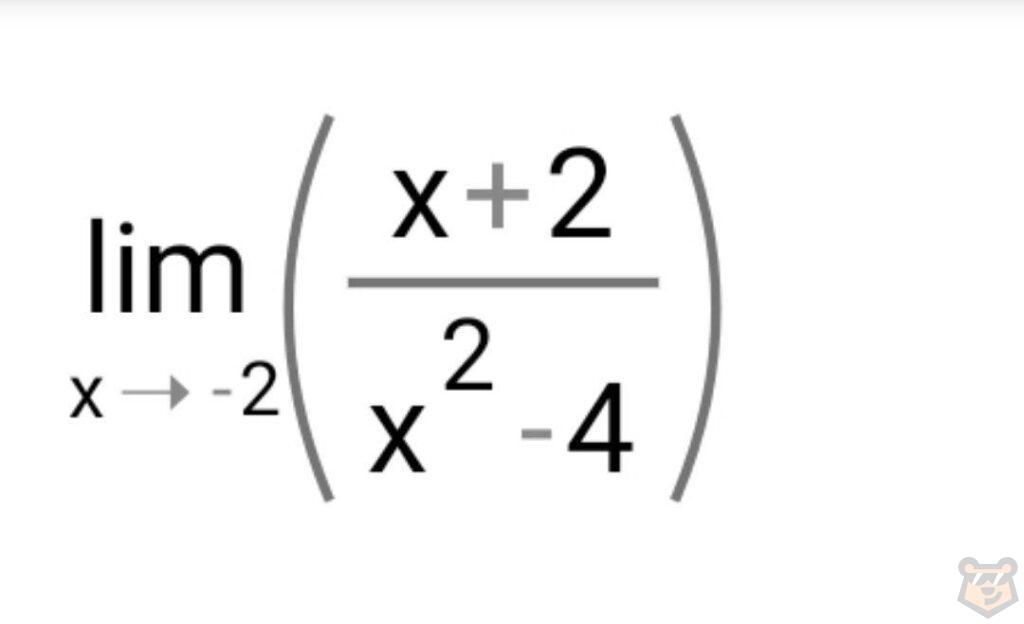
Задание №3.
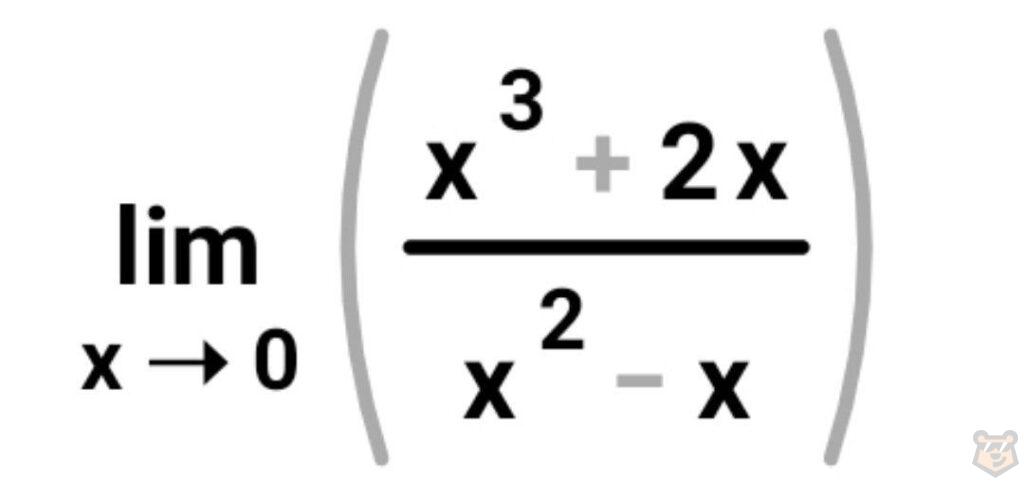
Ответы: 1 — 17/3, 2 — -1/4, 3 — 2.
