Определенный интеграл
Определённый интеграл ещё один инструмент математического анализа. Он нашел широкое применение в разных областях науки. Например, в физике такой интеграл используют для определения объема жидкости или твёрдого тела, в экономике его применяют для оценки доходности инвестиций. А благодаря данной статье мы узнаем как определенный интеграл используется в математике.
Безусловно, данное математическое понятие тесно переплетается с производной, первообразной и неопределенным интегралом, однако имеет свои особые черты.
Но давайте со всем разбираться по порядку.
Определенный интеграл.
Казалось бы определенный интеграл должен быть легче, чем неопределенный. Банально потому что неизвестность и неоднозначность звучат куда хуже, но не тут то было. Если обратимся к нашей трактовке и формуле, то явно сделаем противоположный вывод.

Как можно заметить из формулы данный вид интегралов на письме обозначаем так же как неопределенные, единственное, у нас появляются буквы а и b. Это пределы, ограничения, которые как раз и отличают определенный интеграл от неопределенного. Ведь по работе с первым видом интегралов у нас есть строго ограниченный отрезок.
Думаю, что другое мало кто сможет понять, да и навряд ли кто-то захочет вдаваться в подробности этой жути.
Поэтому переведем наше длинное толкование на более “человеческий” язык:
Определенный интеграл данной нам функции на отрезке а-b — это такой ее предел, который не будет зависим ни от выбора точки, ни от способа разбиение отрезка а-b на части.
Давайте объясним это еще проще. Определенный интеграл это ничто иное, как приращение (изменение) первообразной нашей функции на отрезке а-b.
И по сути представляет собой разность двух первообразных, одна из которых находится из хотя из того, что х=а, а вторая х=b.
Получается, что в таком случае неопределенный интеграл приобретет следующий вид:
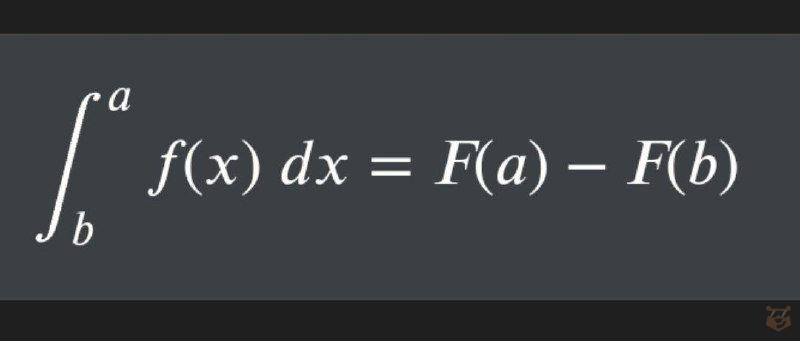
Данное выражение в математике получило название “формула Ньютона-Лейбница”.
Как пользоваться данной формулой ? Рассмотрим на одном примере.
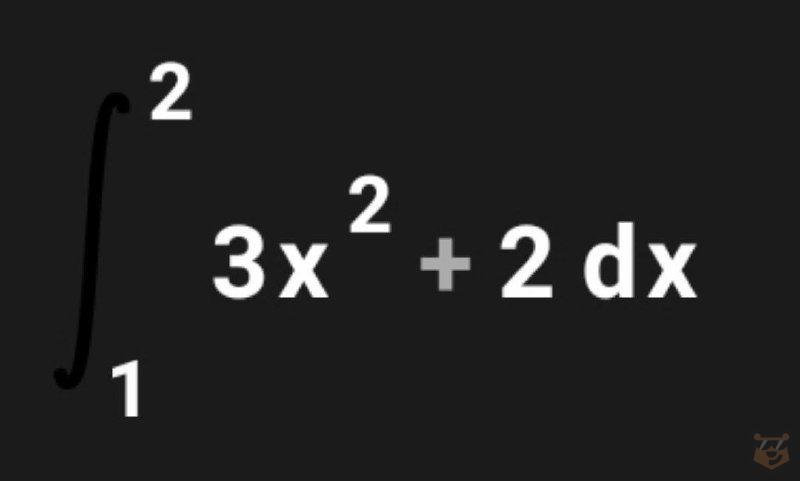
1) Находим неопределенный интеграл (первообразную) нашей функции 3х^2+2. Используем для этого хорошо всем знакомые свойства и прекрасно известную таблицу. Это все мы рассматривали при изучении неопределенных интегралов.
∫ (3х^2+2)dx = ∫ (3х^2)dx + ∫ 2dx
1.1. ∫ (3х^2)dx.
x^n = x^(n+1)/n+1
∫ (3х^2)dx =3х^(2+1)/2+1= 3х^3/3 = х^3
1.2. ∫ 2dx.
k = kx+C
∫ 2dx = 2х
1.3. ∫ (3х^2)dx + ∫ 2dx = х^3 + 2х
2) Воспользуемся данным выражением :
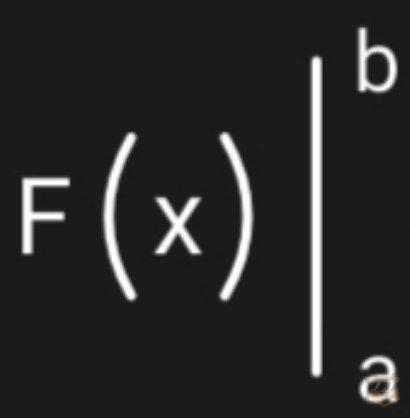
В итоге сделаем такого рода запись:
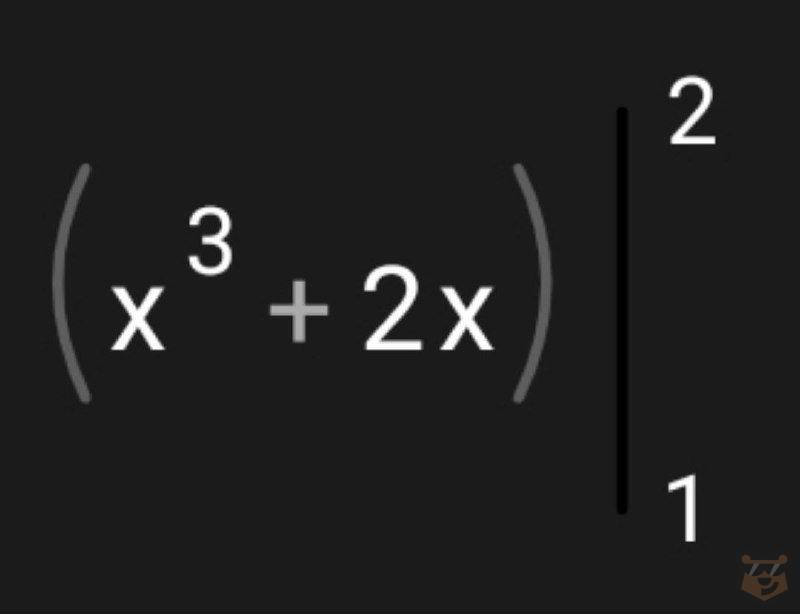
3) Вычисляем с помощью такой формулы:
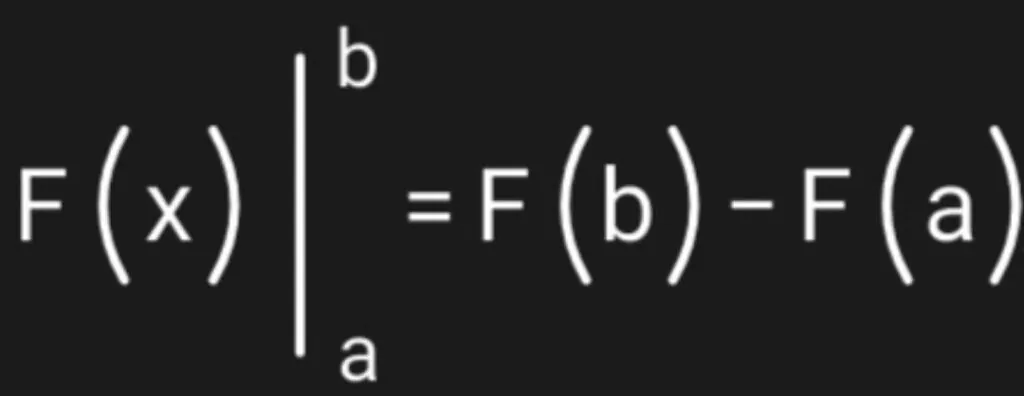
F(a)=F(2)= 2^3 + 2×2= 8 + 4 = 12
F(b)=F(1)= 1^3 + 1×2= 1 + 2 = 3
F(a) — F(b) = 12 — 3 = 9.
Ответ: 9
Для наглядности и простоты понимания запомним это с помощью небольшого мема-подсказки.

Определенный интеграл и площадь фигур.
Предлагаю разобраться как взаимосвязаны определенный интеграл и данный нам отрезок на нашем графике.
Нам дана линейная функция у=2х.
Возьмем 2 точки, составим таблицу и начертим нашу прямую.
| х | 0 | 1 |
| у | 0 | 2 |
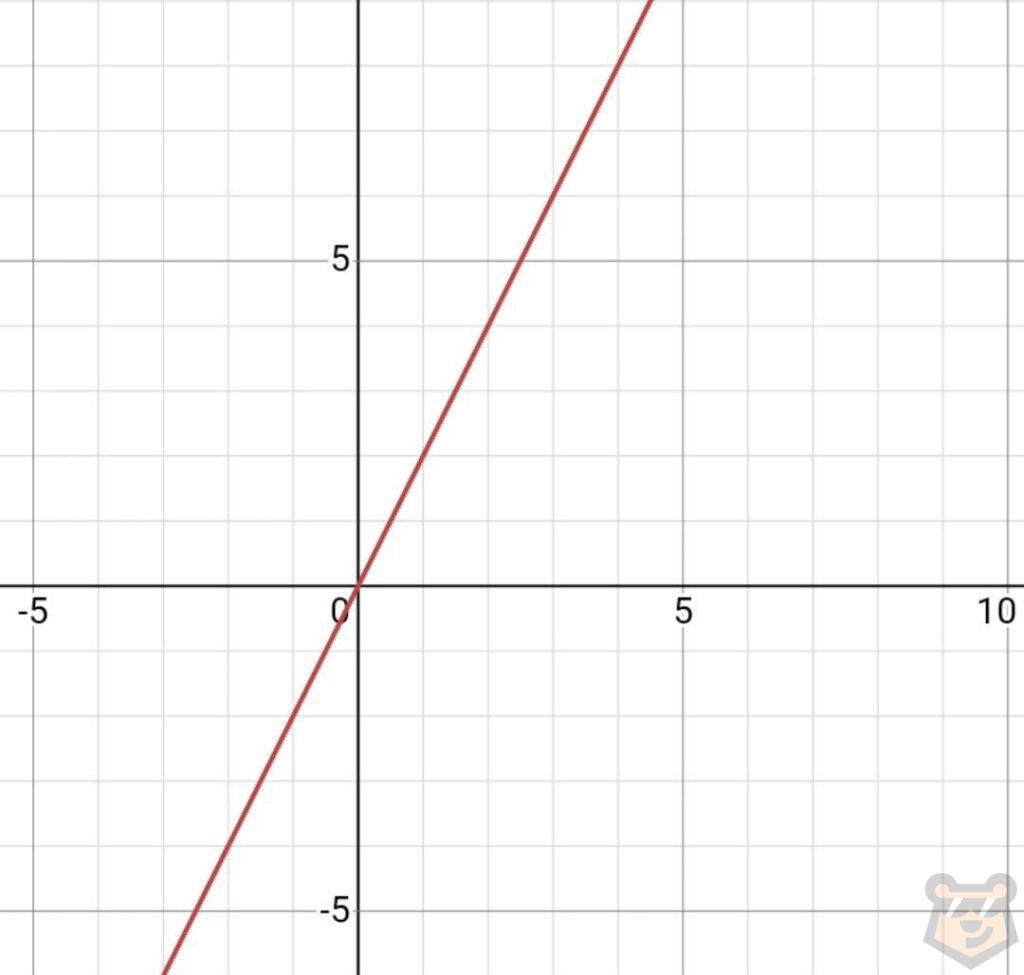
На этом графике отметим точки с координатами (0; 0) и (3;0).
Это будут наши пределы.
Нижний предел (b) равен 0, а верхний предел (а) равняется 3.
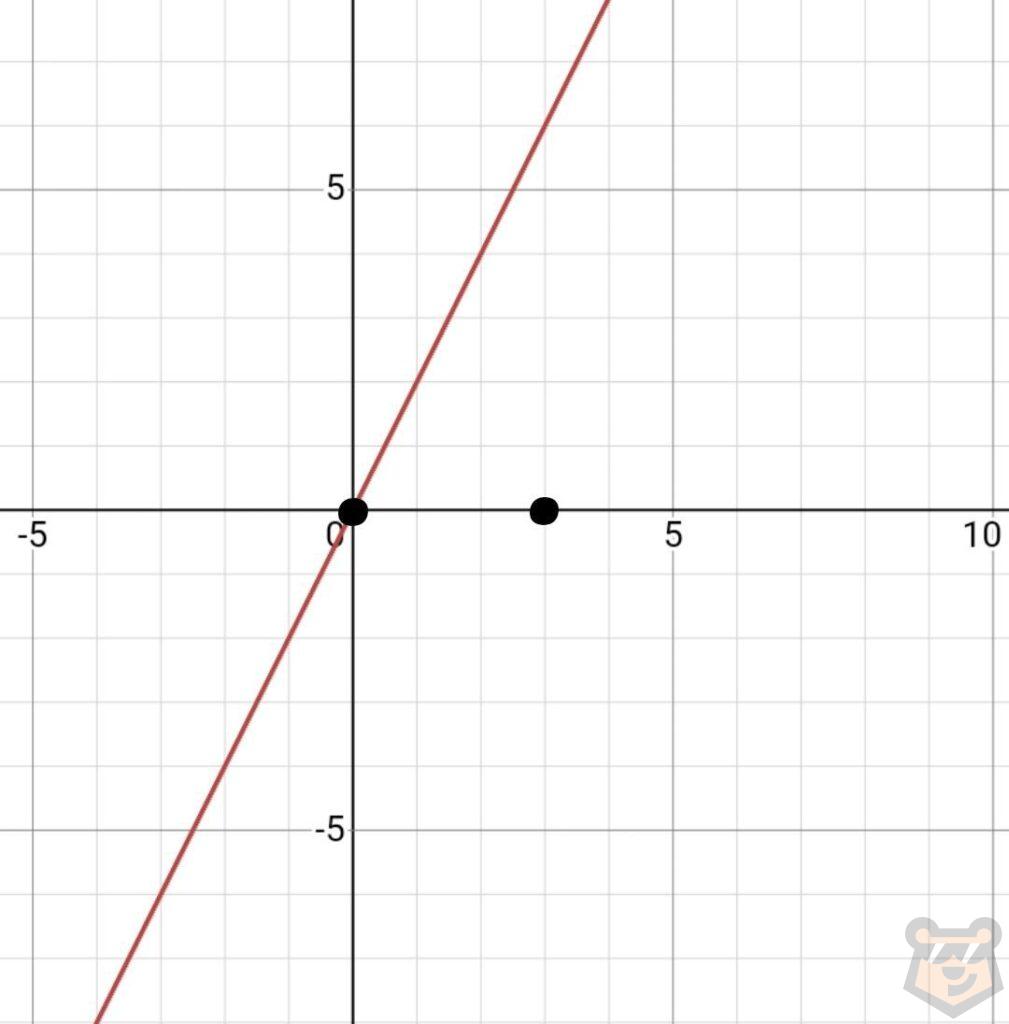
Найдем отрезок прямой, который проходит на интервале оси Ох [0; 3]. Отметим его.
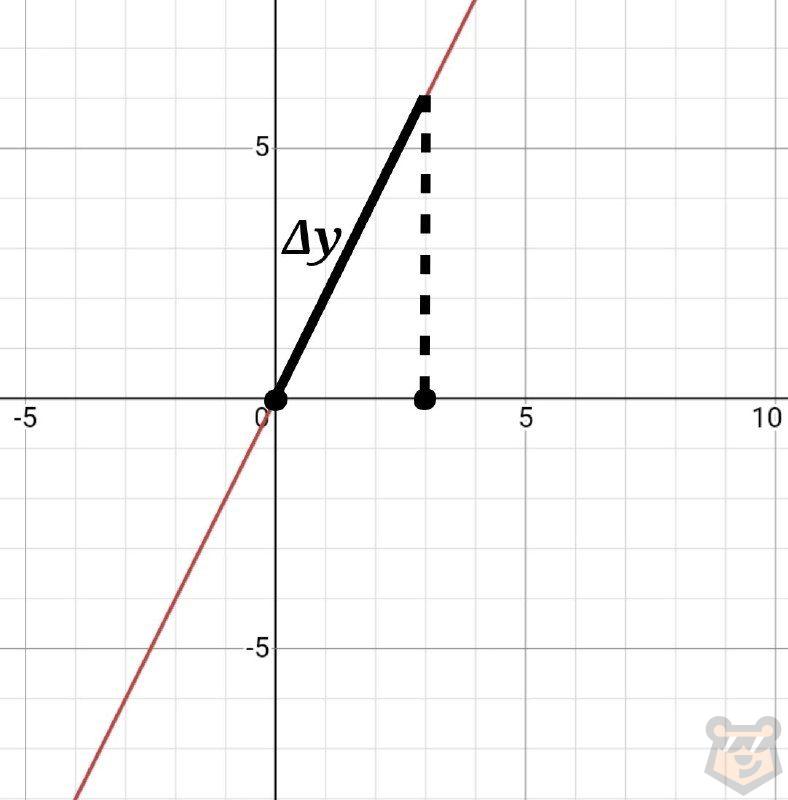
Получается, определенный интеграл с данными пределами будет являться приращением первообразной на этом участке графика. И выглядит он так:
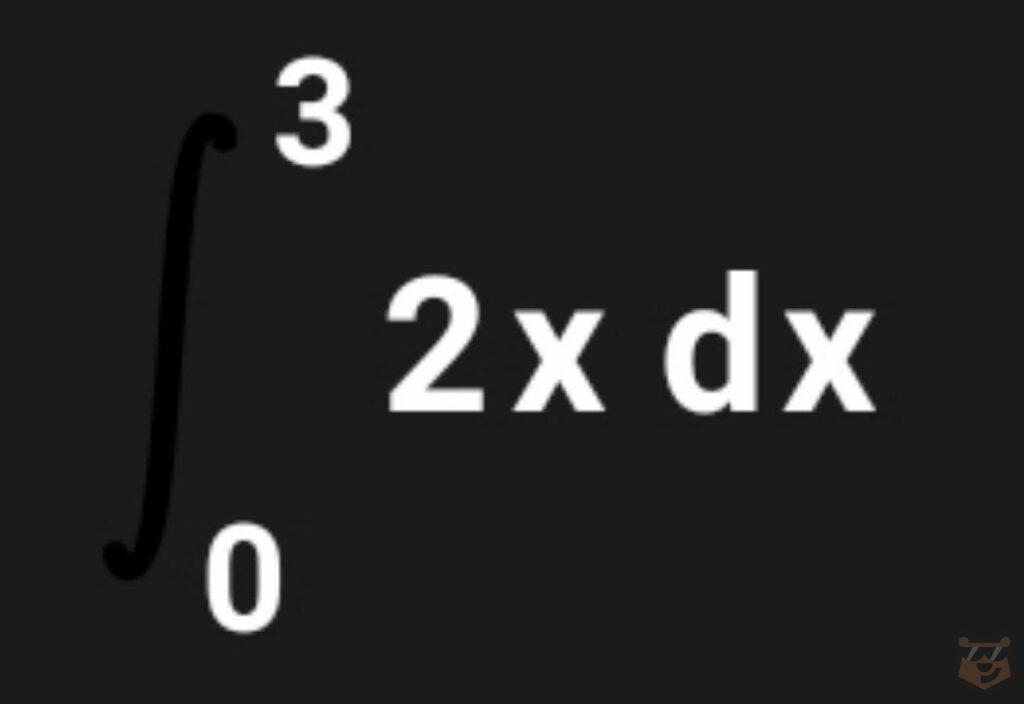
Сделаем все необходимые вычисления.
1) ∫ 2хdx = 2x^(1+1)/(1+1) = 2x^2/2
2) F(a)=F(3)= 3^2 = 9
F(b)=F(0)= 0^2 = 0
F(a) — F(b) = 9 — 0 = 9
Запомним наш интеграл равен 9.
Вернёмся к нашему графику. Проведем прямые через две ранее отмеченные точки (х1=0, х2=3).
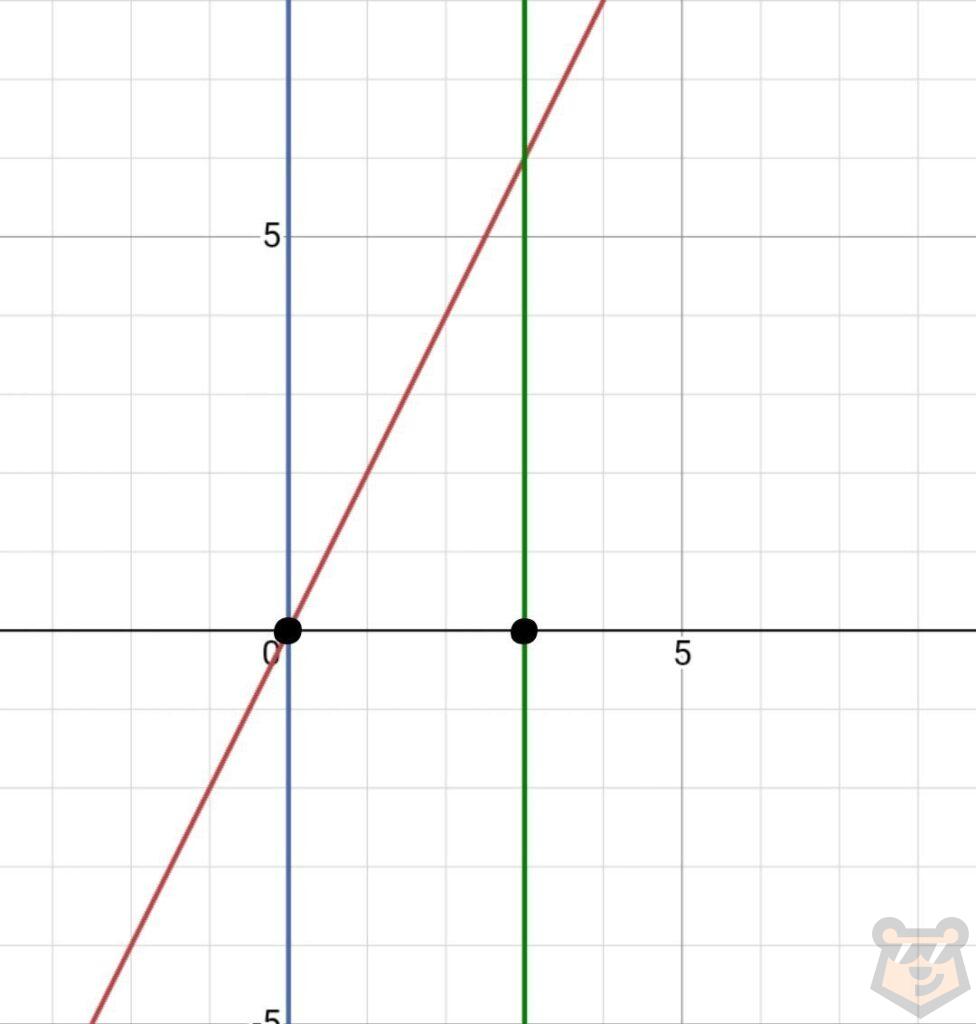
Отметим третью точку, где эти две прямые пересекаются.
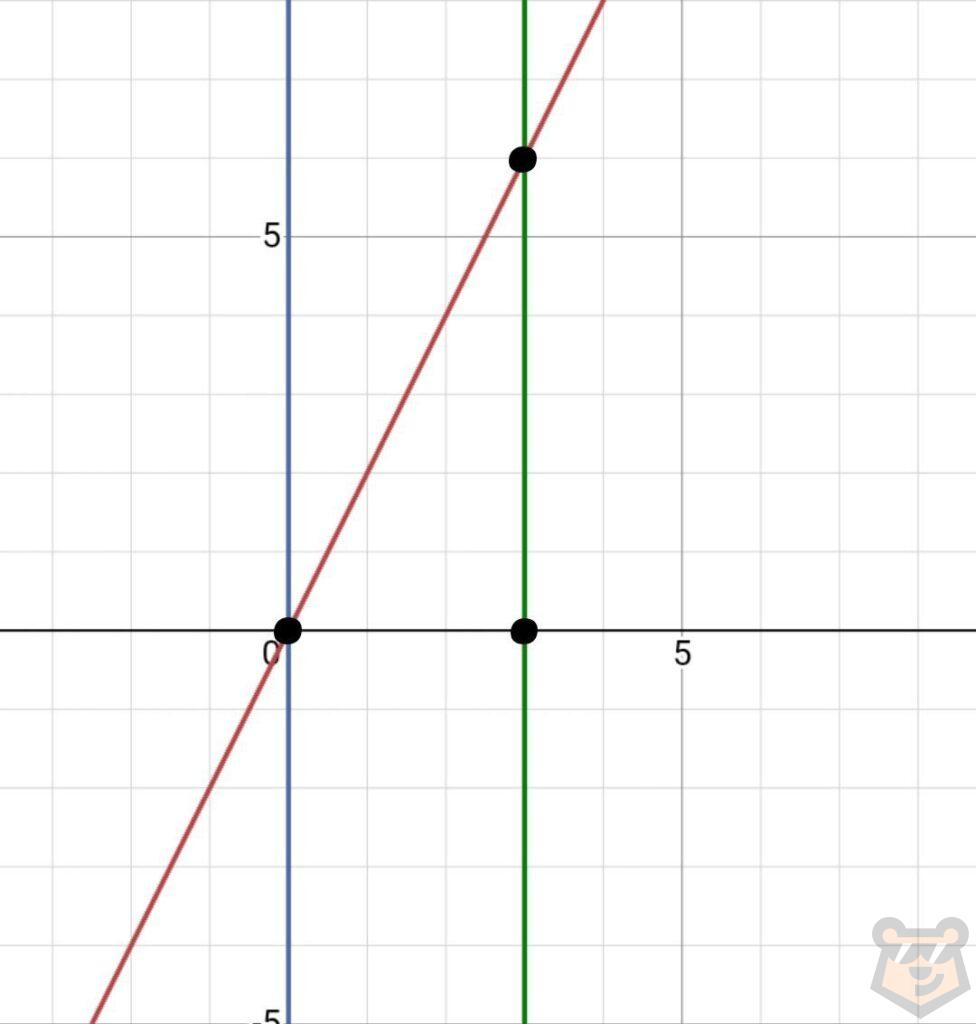
У нас получился треугольник.
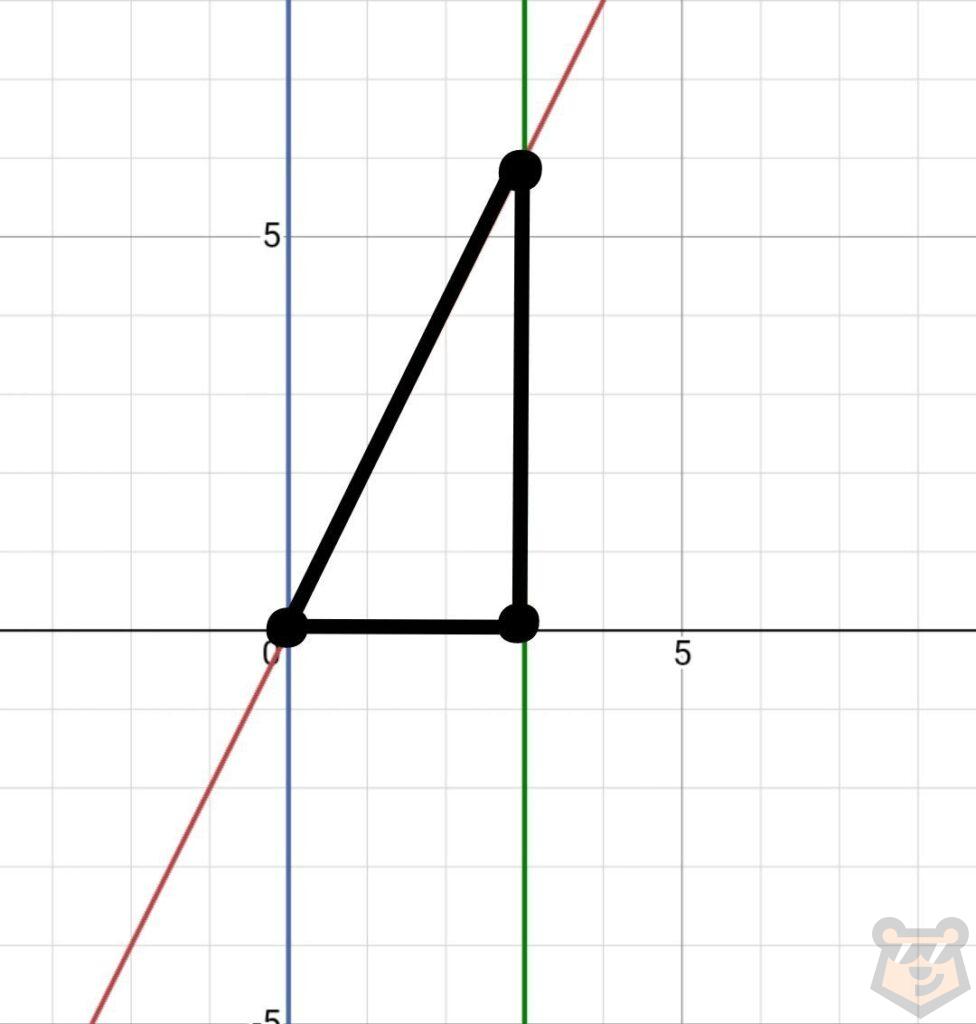
Назовем его АВС и отметим, что он является прямоугольным.
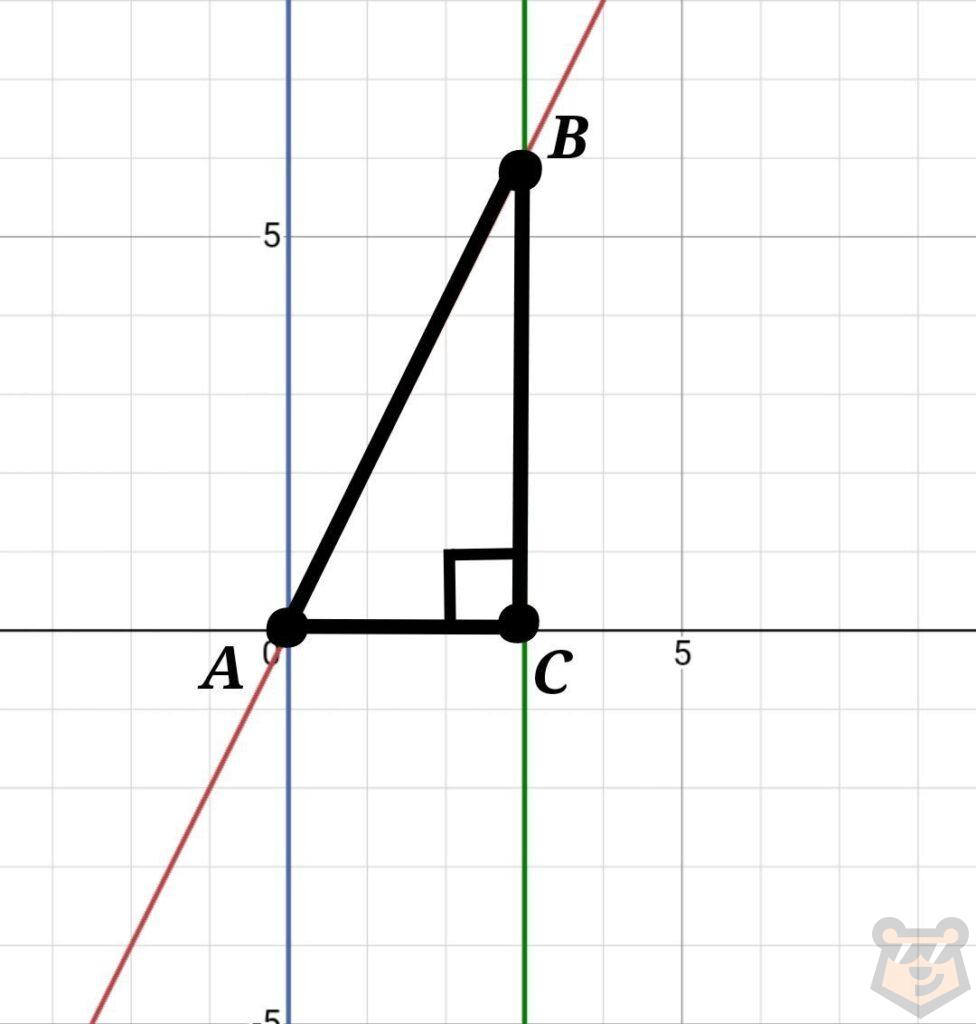
Сейчас вычислим его площадь. Формула для нахождения площади прямоугольного треугольника S=а×b/2.
То есть S равняется половине от произведения катетов.
Посмотрим внимательно на график. Катетами являются АС и BC.
AC=3 BC=6
S= АС × BC / 2 = 6×3/2 = 18/2 = 9
Вспоминаем значение нашего интеграла. 9 = 9. Числа одинаковы.
Можно смело сделать вывод: Площадь фигуры, находящейся под отрезком a-b, равняется определенному интегралу с пределами a и b.
Это будет характерно не только для прямоугольного треугольника, но и для других фигур, будь то трапеция или что-то другое.
Получается, мы можем найти площадь даже такой непривычной фигуры:
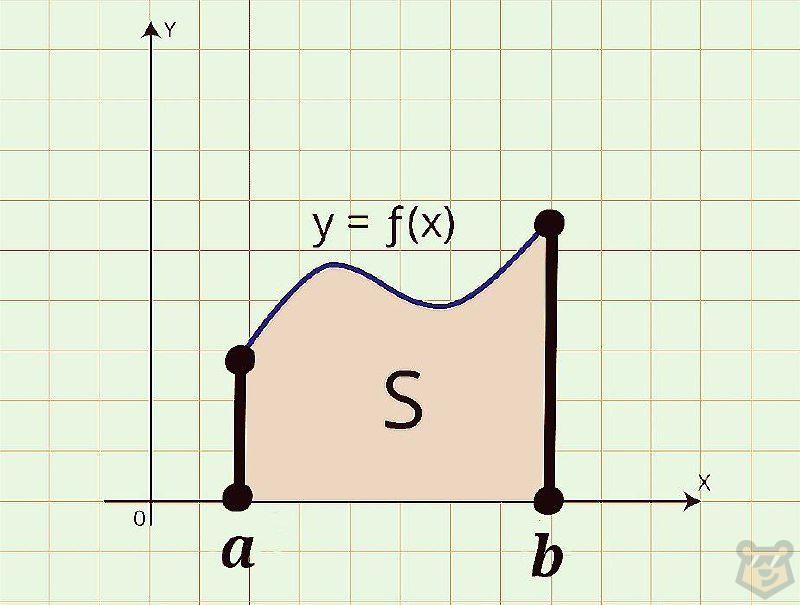
*Данную фигуру и схожие с ней называют криволинейными трапециями.
Для поиска площади таких фигур мы должны научиться правильно составлять неопределенный интеграл по графику, ну и конечно же, уметь решать его без ошибок.
Определенный интеграл и объем тел вращения.
Связь определенного интеграла и объема тела, полученным вращением фигуры под отрезком интеграла, выразили следующей формулой.
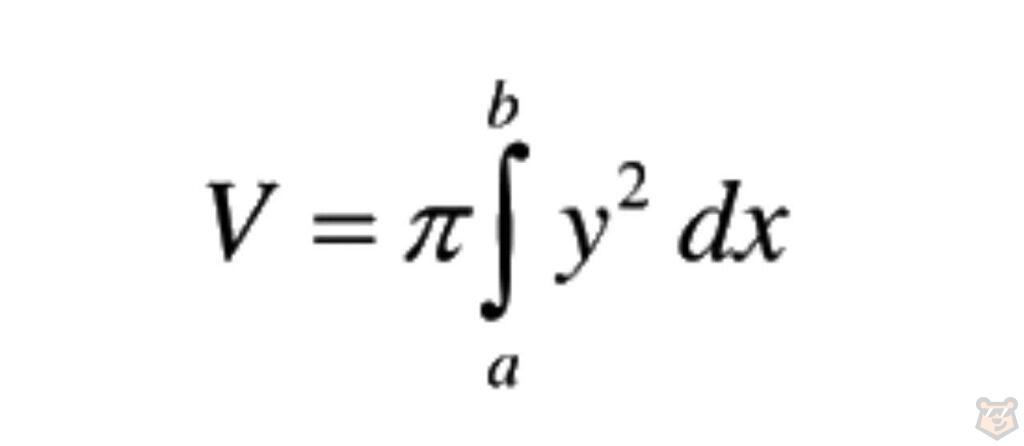
Рассмотрим это на одном простом примере.
Дана функция у=3. Начертим график прямой.
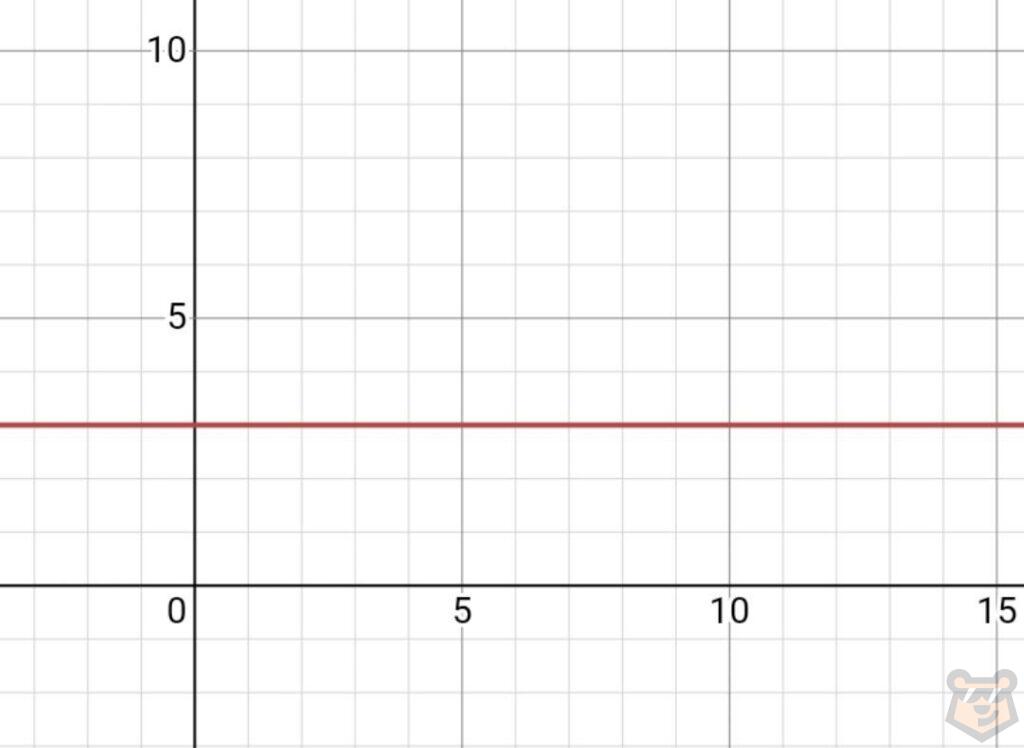
Отметим две точки с координатами (1;0) и (7;0).
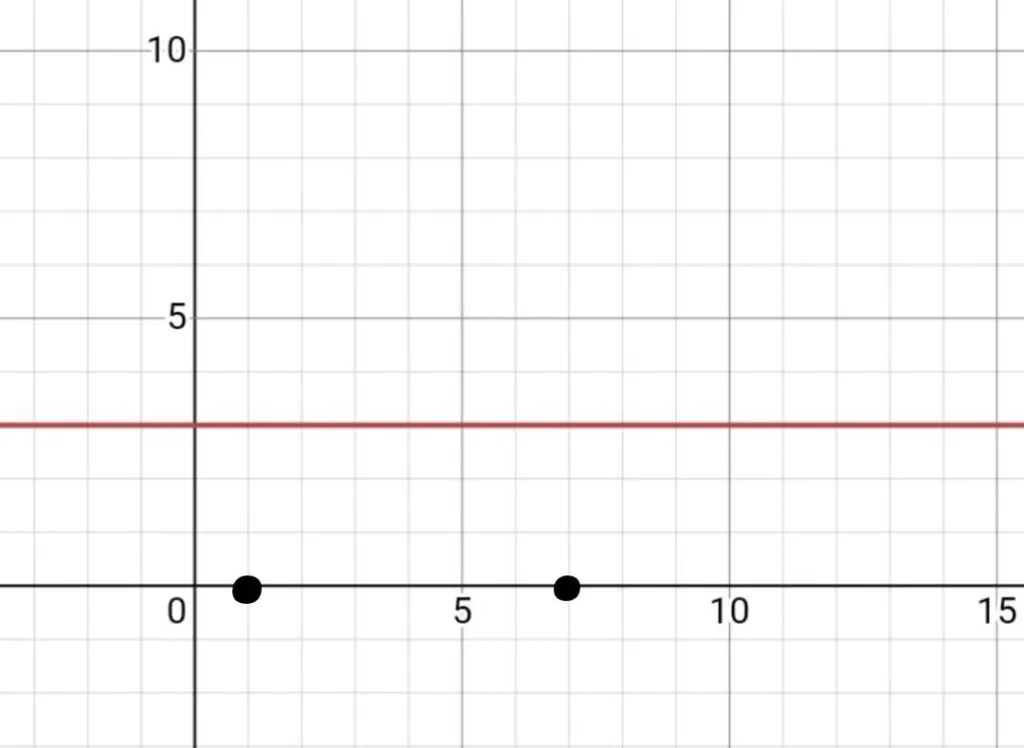
Найдем отрезок прямой, проходящий через наш интервал на оси абсцисс [1;7].
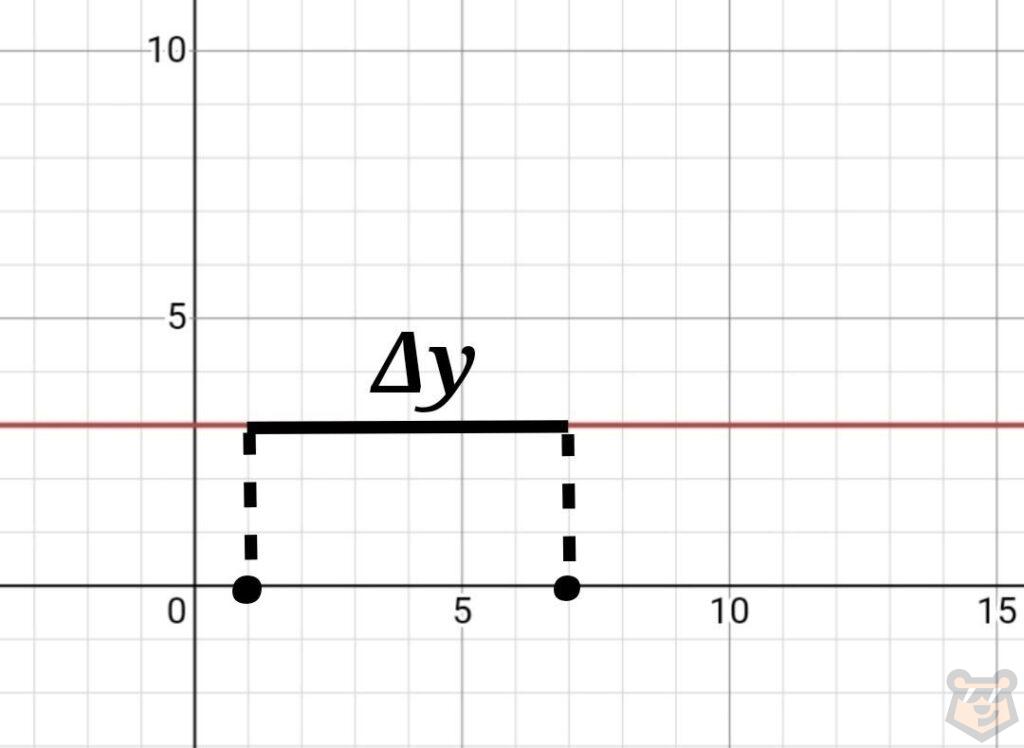
Данный участок и будет являться приращением нашей первообразной.
Запишем наш интеграл. И сделаем решение.
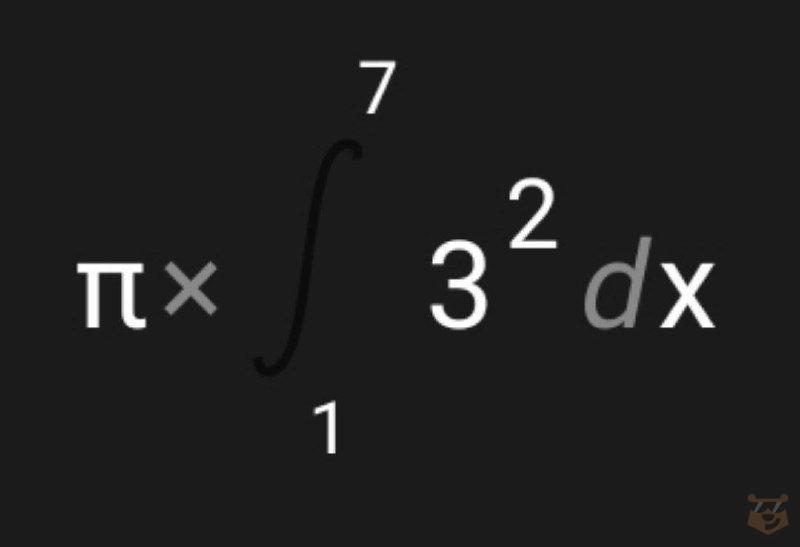
π × ∫ (3^2)dx = π × ∫ 9dx = π × 9x
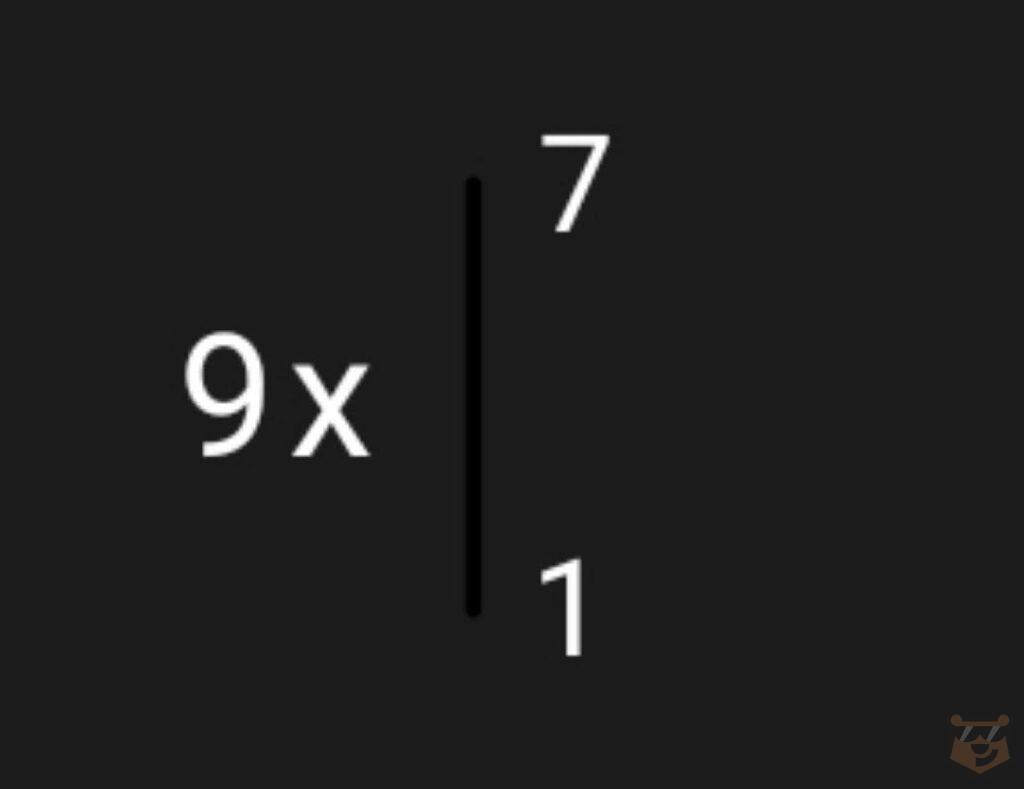
F(a)=F(7)= 7×9= 63π
F(b)=F(1)= 1×9 = 9π
F(a) — F(b) = 63π-9π = 54π
Теперь давайте сделаем вращение нашим прямоугольником вокруг оси Ох. У нас получиться цилиндр.
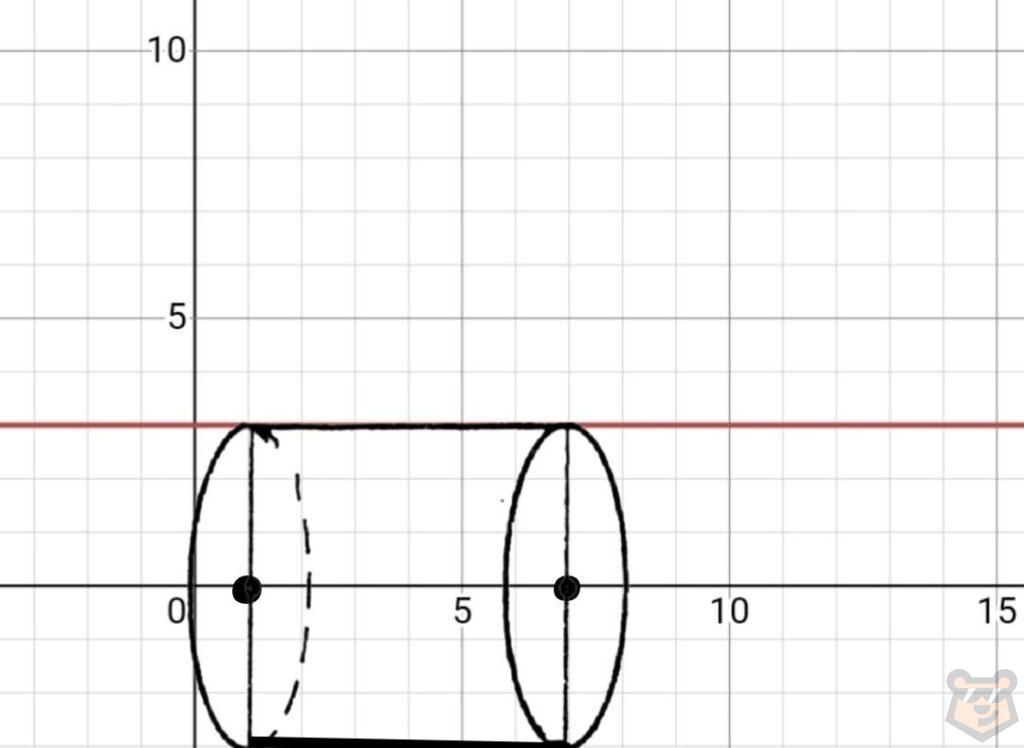
Внимательно рассмотрим его и заметим, что H=∆y, а R=∆x.
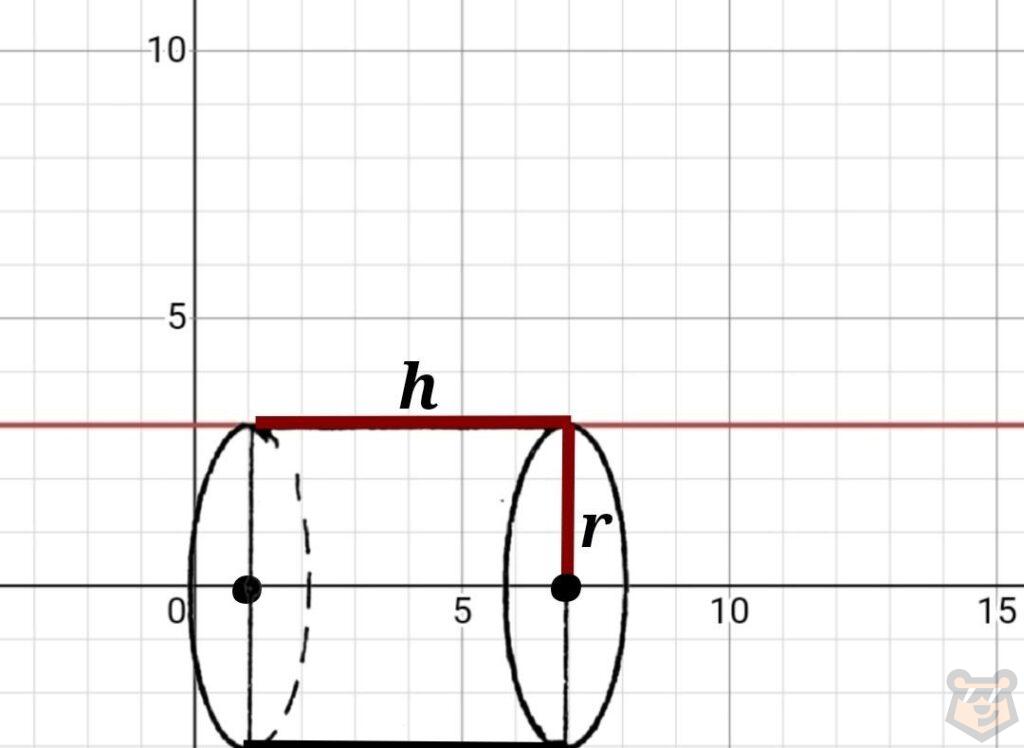
H = ∆y = 7-1 = 6
R =∆x = 3-0 = 3
Найдем объем цилиндра по формуле V= π×R^2×H.
V= π×3^2×6 = π×9×6= 54π.
Значения является одинаковыми. 54π = 54π.
В данном случае мы поняли взаимосвязь тел вращения и определенного интеграла, убедились в правильности формулы и научились ей пользоваться.
Естественно, такой особенностью интеграла обычно пользуются для поиска объема более сложных фигур, например, тех, что представлены на картинках.
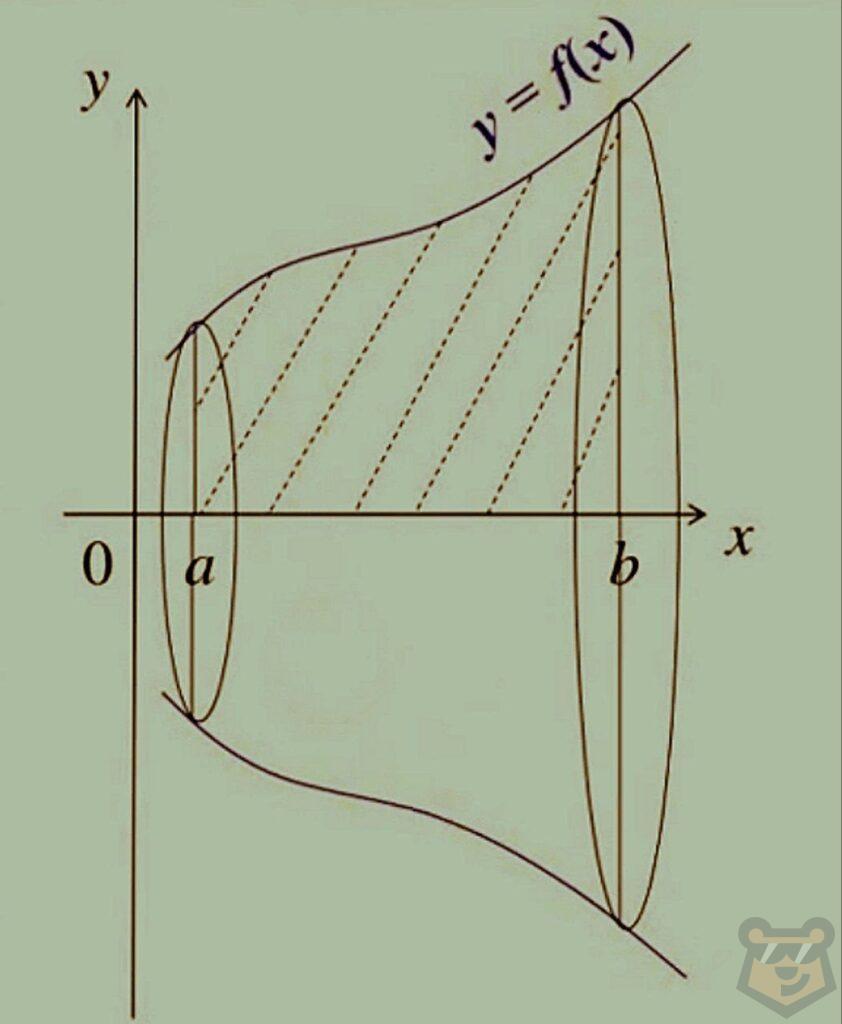
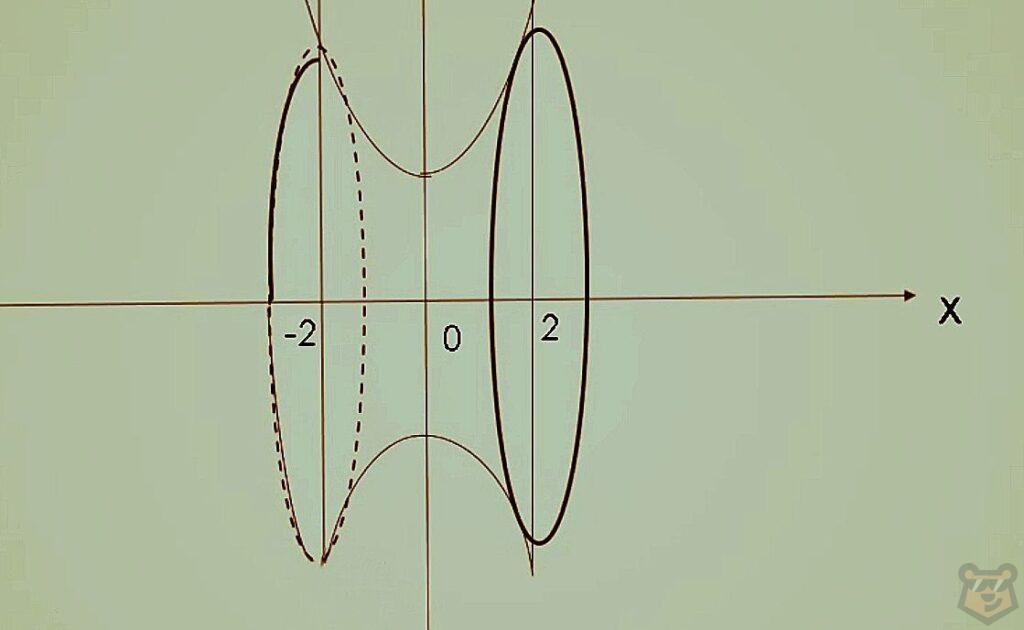
Практическая часть.
Перейдем с теории на практику, дабы все запомнить и надолго закрепить у себя в памяти.
Задание №1. Вычислите определенный интеграл:
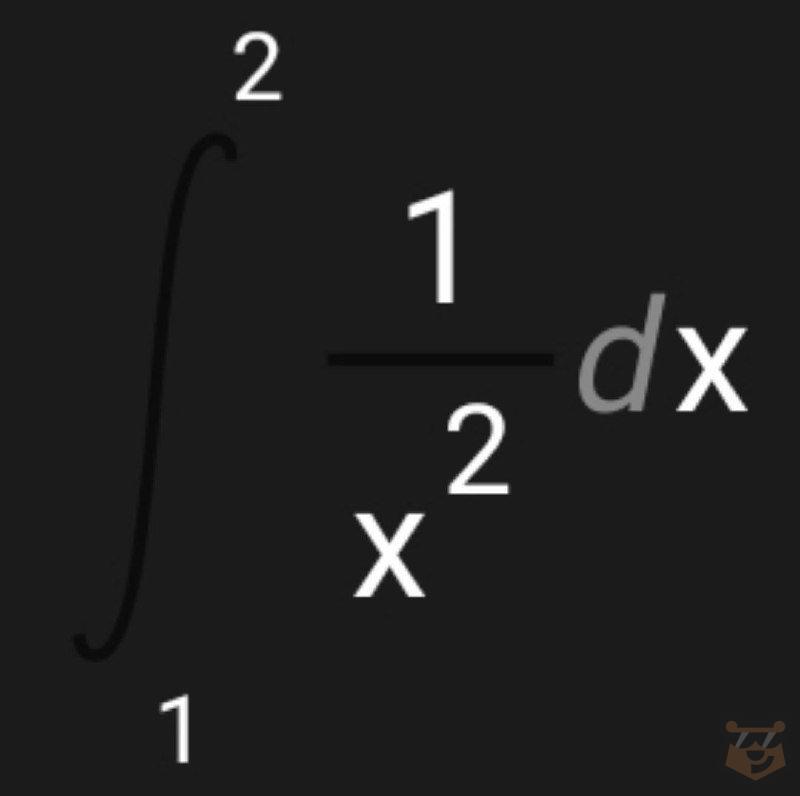
Решение. В таблице нет такого случая, поэтому нам необходимо преобразовать нашу функцию. Выразим 1/х^2, как х^(-2).
Теперь используем табличную формулу.
x^n = x^(n+1)/n+1
∫ х^(-2)dx= x^(-2+1)/-2+1 = x^(-1)/-1 = — x^(-1)= -1/x
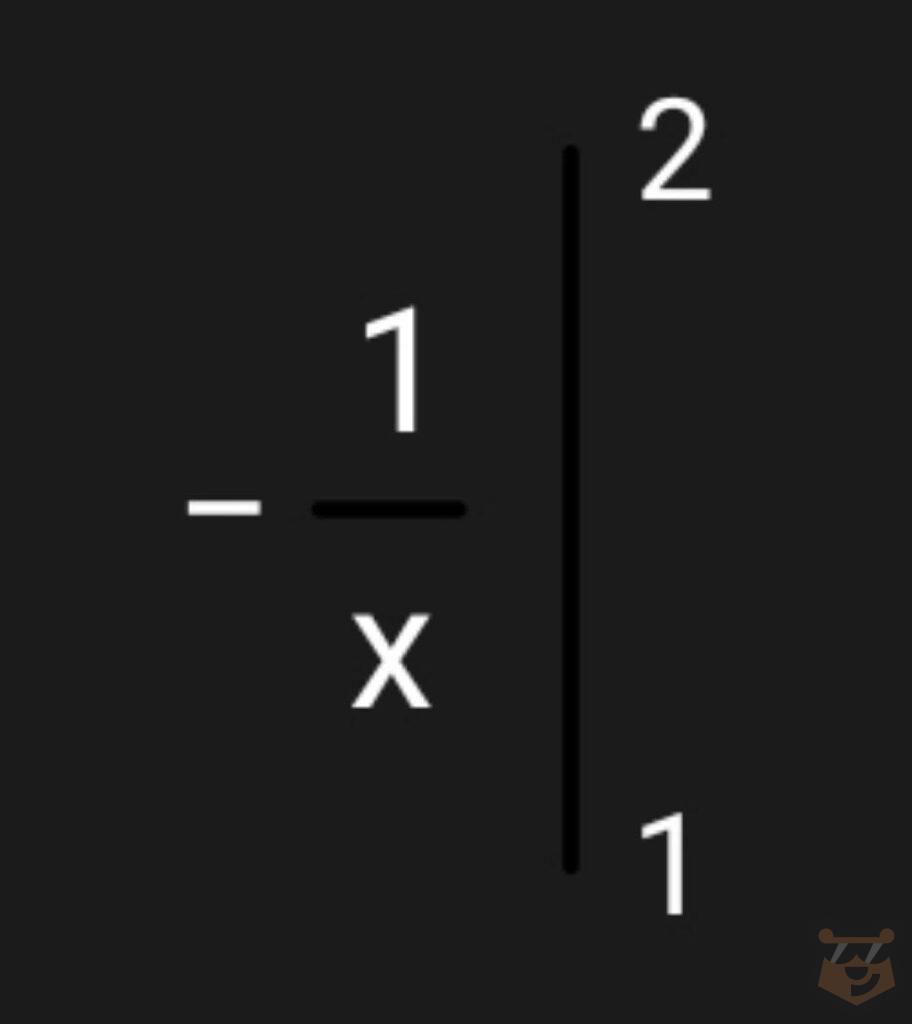
F(a) — F(b) = F(2) — F(1) = -1/2- (-1/1)= -1/2 — (-1) = -1/2 + 1 = 1/2.
Ответ: 1/2.
Задание №2. Найдите чему равен интеграл:
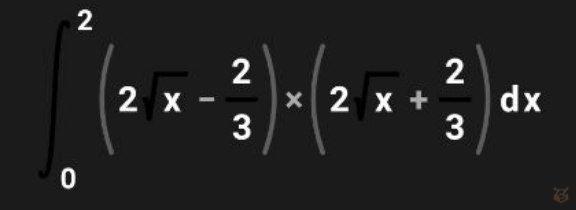
Решение. 1) Используя формулу сокращенного умножения и преобразуем нашу запись.
(2√х- 2/3)(2√х + 2/3)=(2√х)^2 — (2/3)^2=4х — 4/9
2) Получим ∫ 4х — 4/9dx.
3) Превратим наш интеграл в два отдельных.
∫ 4х — 4/9dx = ∫ 4xdx — ∫ 4/9dx
4) ∫ 4xdx = 4x^(1+1)/(1+1)=4x^2/2=2x^2
∫ 4/9dx = 4/9x
∫ 4xdx — ∫ 4/9dx = 2x^2 — 4/9x
5) Записываем
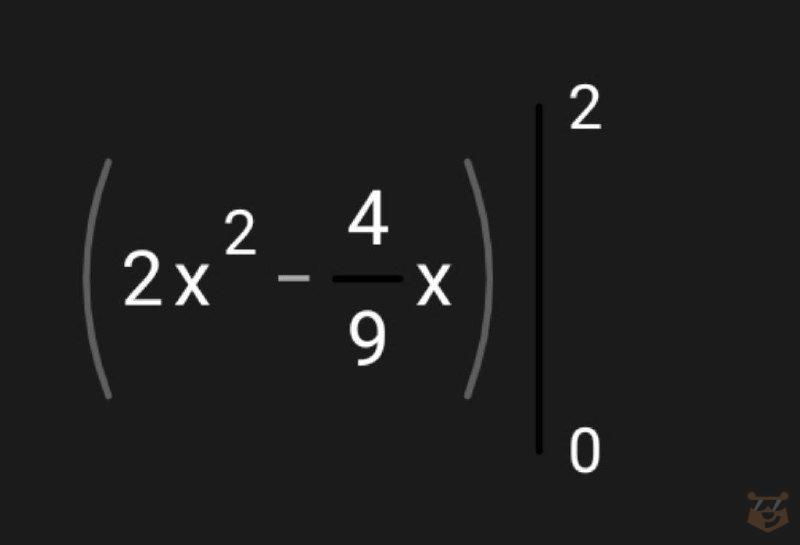
6) Решаем F(a) — F(b)
F(a) — F(b) = F(2) — F(0) = (2×(2^2) — 4/9×2) — 2×0^2 — 4/9×0 = 8 — 8/9 — 0 = (8×9 — 8)/9 = (72-8)/9 = 64/9.
Ответ: 64/9.
Здание №3. Найдите площадь фигуры ограниченной графиками следующих функций у1=х^3+2, y2=-6, х1=-2, х2=2.
Решение. Во-первых, из двух наших функций составим одну. Сделаем это следующих образом.
f(x)=y1-y2=х^3+2-(-6)=х^3+2+6= х^3+8.
Во-вторых, найдем а и b. Нашими ограничениями по оси Ох будут данные нам в условиях прямые х=-2, х=2. Получается верхний предел равен 2, а нижний -2.
В-третьих, составим наш интеграл исходя из того, что f(x)=х^3+8, а=2, b=-2.
Получим:
В-четвертых, решим полученное выражение.
4.1. ∫ х^3+8dx = ∫ х^3dx + ∫ 8dx
4.2. ∫ х^3dx = х^(3+1)/(3+1) = х^4/4
4.3. ∫ 8dx = 8x
4.4. ∫ х^3dx + ∫ 8dx = х^4/4 + 8x
4.5.
4.6. F(a) — F(b) = F(2) — F(-2) = (2^4/4 + 8×2) — ((-2)^4/4 + 8×(-2)) = (16/4 + 16)-(16/4-16)= 16/4 + 16-16/4 + 16= 16+16 = 32 кв.ед.
Ответ: 32 кв.ед.
Задание №4. Вычислите объем тела, которое ограничено прямыми у=4 и у=х^2.
Решение. Во-первых, представляем из данных двух функций одну. Для этого воспользуемся таким выражением у=(у1)^2-(у2)^2. Тогда наша функция будет иметь вид у=(4)^2-(х^2)^2=16-х^4-.
Во-вторых, находим точки пересечения нашего тела с осью Ох.
2.1. 16-х^4-=0.
16=х^4
х^4=16
х1=2
х2=-2
2.2. Получается, а=2, b=-2.
В третьих, запишем интеграл опираясь на полученные данные и на нашу формулу. Выходит так:
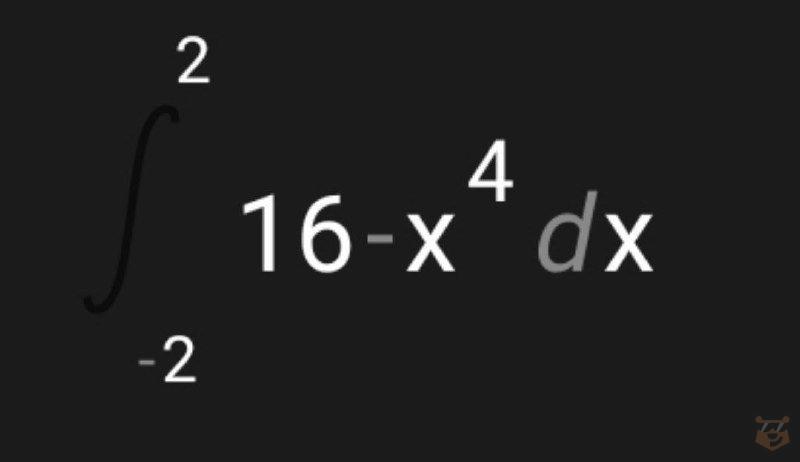
В-четвертых, решаем интеграл.
4.1. Разделим наш интеграл на части ∫ 16 — х^4dx и найдем две отдельных первообразных.
∫ 16dx-∫ х^4dx.
4.3. ∫ 16dx = 16x
4.3. ∫ х^4dx= х^(4+1)/(4+1)=х^5/5
4.4. ∫ х^4dx — ∫ 16dx = х^5/5 — 16x
4.5. Делаем запись.
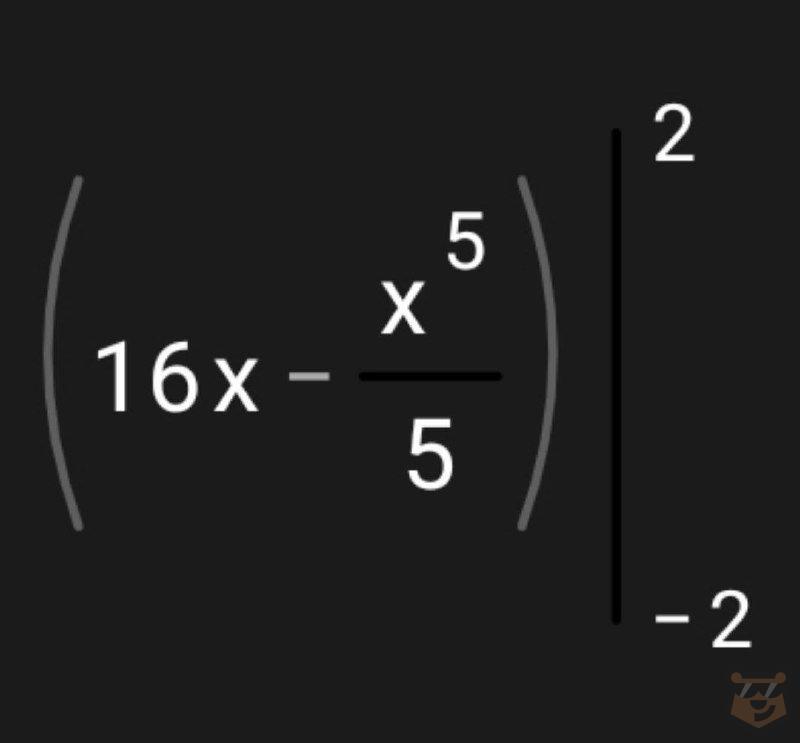
4.6. Вычисляем F(a) — F(b).
F(a) — F(b) = F(2) — F(-2)= (16×2 — 2^5/5) — (16×(-2) — (-2)^5/5) = (32 — 32/5) — (-32 — (-32/5)) = ( 32 — 32/5) — (32 + 32/5) = 32 — 32/5 + 32 — 32/5 = 64 — 64/5 = (64×5-64)/5 = (320 — 64)/5 = 512/5
4.7. π × 512/5= 512π/5 куб.ед.
Ответ: 512π/5 куб.ед.
Задания по данному разделу, которые встречаются на ЕНТ.
Задачи по теме «Определенный интеграл» присутствуют лишь в профильной математике. Есть несколько их типов. Поэтому давайте рассмотрим и решим то, что может нам встретиться.
Задание №1. Найдите неопределенный интеграл.
Решение. 1. Для начала необходимо расписать нашу дробь.
√х + 2х^2 — 4 / х^2 = √х/х^2 + 2х^2/х^2 — 4 / х^2 dx .
1.1. √х/х^2.
Представим √х как х^(1/2)
Выходит √х/х^2 = х^(1/2)/х^2 = х^(1/2-2) = х^(-3/2)
1.2. 2х^2/х^2 = 2
1.3) 4 / х^2
Представим это как 4 × 1/х^2. Распишем наш знаменатель как х^(-2). Выходит, что 4 / х^2 = 4 × х^(-2)
1.4. ∫ (х^(-3/2) + 2 + 4 × х^(-2))dx
2. Представим наш большой интеграл как три отдельных.
∫ (х^(-3/2)dx + ∫ 2dx+ ∫ 4 × х^(-2)dx
2.1. ∫ (х^(-3/2)dx.
∫ (х^(-3/2)dx= х^(-3/2+1)/(-3/2+1) = х^(-1/2)/(-1/2) = -2 × х^(-1/2)= -2 × х^(-1/2) =
=-2 × √х^(-1)= -2 × √(1/х) = -2 × √1/√х = -2 × 1/√х = —2/√х
2.2. ∫ 2dx = 2х.
2.3. ∫ 4 × х^(-2)dx.
Воспользуемся выражением ∫ k×f(x)dx =k× ∫ f(x)dx.
Тогда ∫ 4 × х^(-2)dx = 4 × ∫ х^(-2)dx.
∫ х^(-2)dx = х^(-2+1)/(-2+1) = х^(-1)/(-1) = — х^(-1) = — 1/х.
4 × ∫ х^(-2)dx = 4 × — 1/х = — 4/х
2.4. ∫ (х^(-3/2) + 2 + 4 × х^(-2) ) dx = -2/√х + 2х — 4/х
2.5. Тогда мы должны сделать следующую запись:
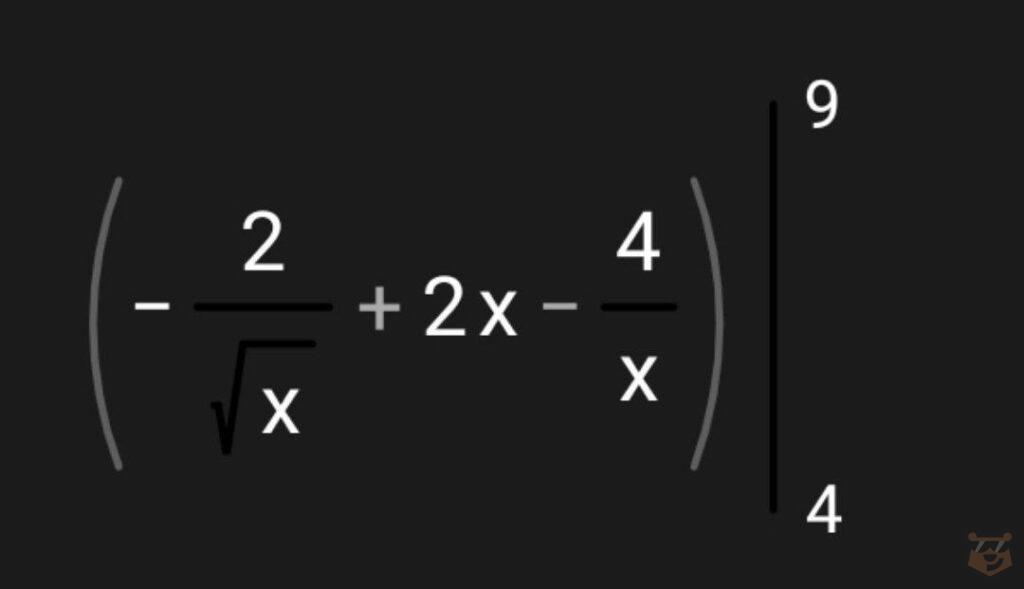
2.6. Вычисляем дальше.
F(a) — F(b) = F(9) — F(4) = (-2/√9 + 2×9 — 4/9) — ( -2√4 + 2×4 — 4/4) = (-2/3 +18 -4/9) — (-1 + 8 -1) = -2/3 +18 -4/9 — 6 = (-2×3 + 18×9 — 4 — 6×9)/9 = (-6 + 162 -4 — 54)/9 = 98/9.
Ответ: 98/9.
Задание №2. Чему равна площадь фигуры, ограниченной линиями у=-3 и у=х^2+2х-3 ?
Решение.
Во-первых, нам опять нужно из данных двух функций как бы “склеить” одну.
1.1. Запись нужно сделать тем же образом: -3-(х^2+2х-3).
1.2. Теперь раскроем скобки. Перед ними стоит минус, значит все знаки в скобках необходимо поменять на противоположные. Тогда выйдет: -3-х^2-2х+3.
1.3. Теперь приводим подобные. Получается, нужно зачеркнуть 3 и -3. Ведь -3+3=0.
1.4. В итоге мы получили функцию у=-х^2-2х.
Во-вторых, мы должны найти пересечения нашей функции с осью абсцисс, которые будут являться нашими пределами. Ведь в условиях нам нужные прямые не указали.
Для этого не обязательно чертить график. Ведь если вспомнить, то функция пересекается с осью Ох когда наш у, то есть значение самой функции, равно нулю.
Воспользуемся данным свойством, чтобы не тратить время на чертеж графика, построение которого иногда может быть достаточно трудным.
2.1. В таком случае выходит, что -х^2-2х=0.
2.2. Решим данное уравнение. Вынесем общий знаменатель -х за скобку.
-х × (х+2)=0.
2.3. Смотрим внимательно на наше уравнение. Для того чтобы при перемножение двух частей получился нуль, нужно чтобы значение хотя бы одной компоненты равнялась нулю.
То есть мы приравняем и одну, и вторую часть к нулю, а потом найдем х.
1) -х = 0 х1=0
2) х+2=0 х2=-2
2.4. Таким образом, мы нашли наши пределы.
Верхний предел равняется 0, а нижний предел равен -2.
В-третьих, нам надо записать наш интеграл с учётом того, что а=0 , b=-2, у=-х^2-2х. Тогда получим следующее:
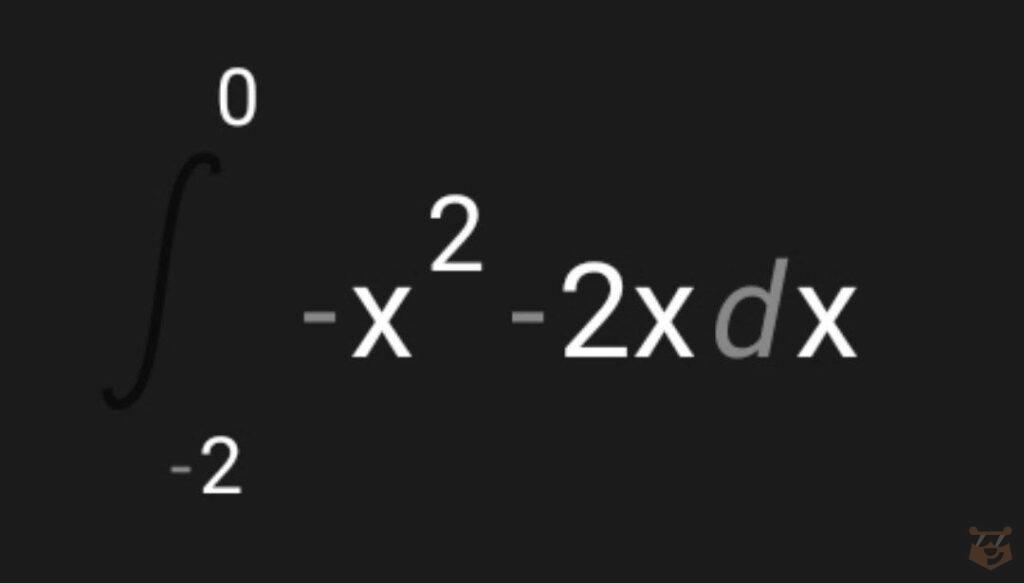
В-четвертых, делаем решение интеграла.
4.1 ∫ (-х^2-2х)dx = ∫ (-х^2)dx — ∫ (2х)dx
4.2. ∫ (-х^2)dx = (-х^(2+1)/(2+1)=-х^3/3.
4.3. ∫ (2х)dx= 2х^(1+1)/(1+1) = 2х^2/2=x^2
4.4. ∫ (-х^2)dx — ∫ (2х)dx = -х^3/3 — x^2
4.5. Делаем такого рода запись.
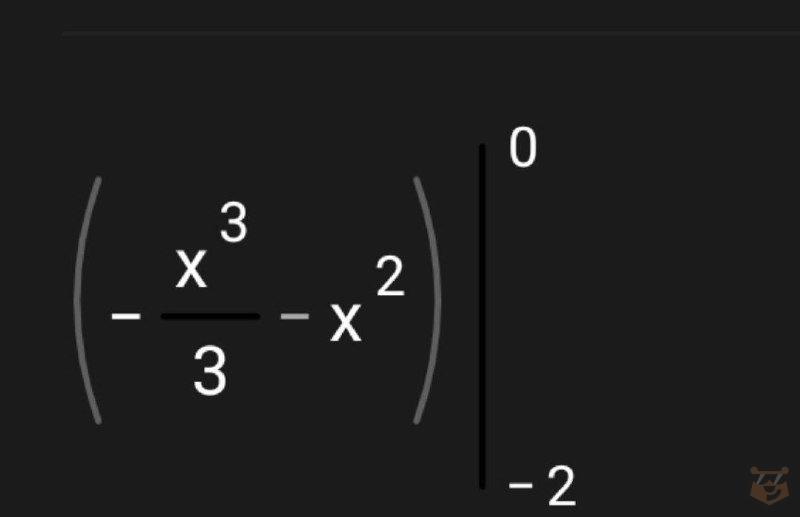
4.6. Вычисляем F(a) — F(b).
F(a) — F(b) = F(0) — F(-2) = (-0^3/3 — 0^2) — ( -(-2)^3/3 — (-2)^2)= 0 — 0 — (-(-8/3) — 4) = 0 — (8/3 -4) = 0 — 8/3 +4 = -8+ 4×3/3 = -8+12/3=4/3.
Ответ: 4/3 кв.ед.
Задание №3. Определите объем тела, ограниченного двумя параболами: у=х^2+2 и у=-х^2+10.
Решение.
1. Составим одну функцию.
у=(у1)^2-(у2)^2= (-х^2+10)^2 — (х^2+2)^2
Воспользуемся формулами сокращенного умножения.
1.1. (-х^2+10)^2= (-х^2)^2 — 2×10×х^2 + 10^2= х^4 — 20х^2 + 100
1.2. (х^2+2)^2= (х^2)^2 + 2×2×х^2+ 2^2 = х^4 + 4х^2 +4
1.3. у=(х^4 — 20х^2 + 100) — (х^4 + 4х^2 +4) = х^4 — 20х^2 + 100 — х^4 — 4х^2 — 4 = х^4 — х^4 — 20х^2 — 4х^2 + 100 — 4 = 96 — 24х^2.
2. Найдем пересечения данных двух парабол для того, чтобы определить наш интервал на оси абсцисс.
2.1. Для этого составим такое равенство у1=у2.
х^2+2 = -х^2+10.
2.2. Решаем.
х^2 + х^2 = 10 -2
2х^2 = 8
х^2 = 4
х1 = 2
х2 = -2
а= 2
b= -2
3. Составляем наш интеграл учитывая полученные данные.
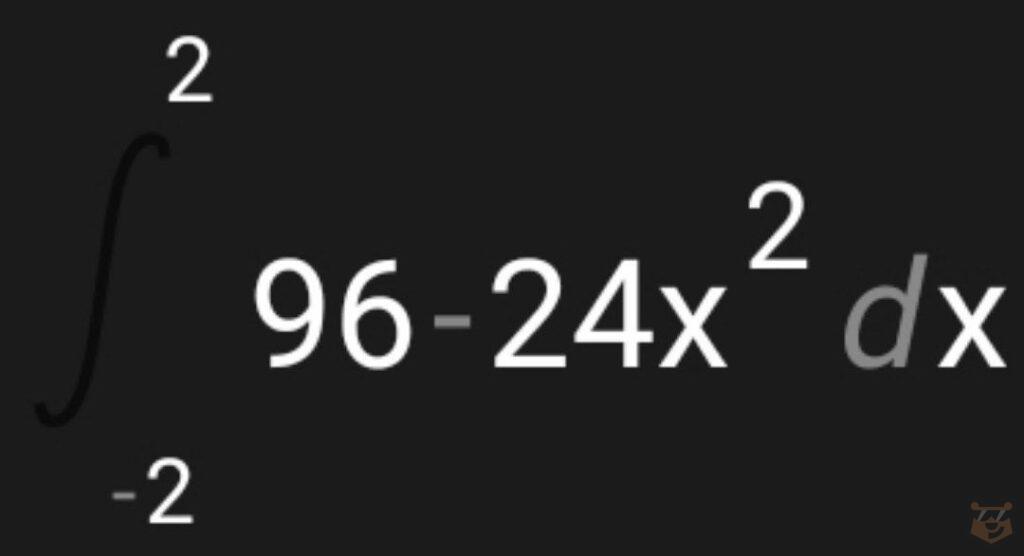
4. Вычисляем интеграл.
4.1. ∫ (96 — 24х^2)dx = ∫96dx — ∫24х^2dx
4.2. ∫96dx = 96x
4.3. ∫24х^2dx = 24х^(2+1)/(2+1) = 24^3/3 = 8x^3
4.4. ∫96dx — ∫24х^2dx = 96x — 8x^3
4.5.
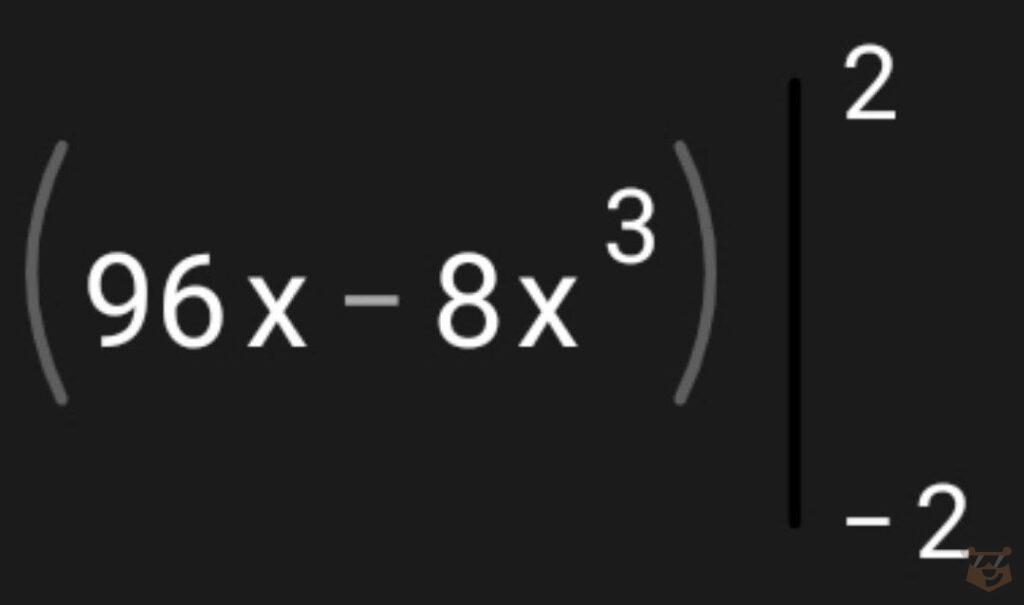
4.6. F(a) — F(b) = F(2) — F(-2) = (96×2 — 8×2^3) — ( 96×(-2) — 8×(-2)^3)= 192 — 64 — ( -192 +64) = 192 — 64 + 192 — 64 = 256
4.7 π×256=256π
Ответ: 256π куб.ед.
Задания для самопроверки:
Задание№1.
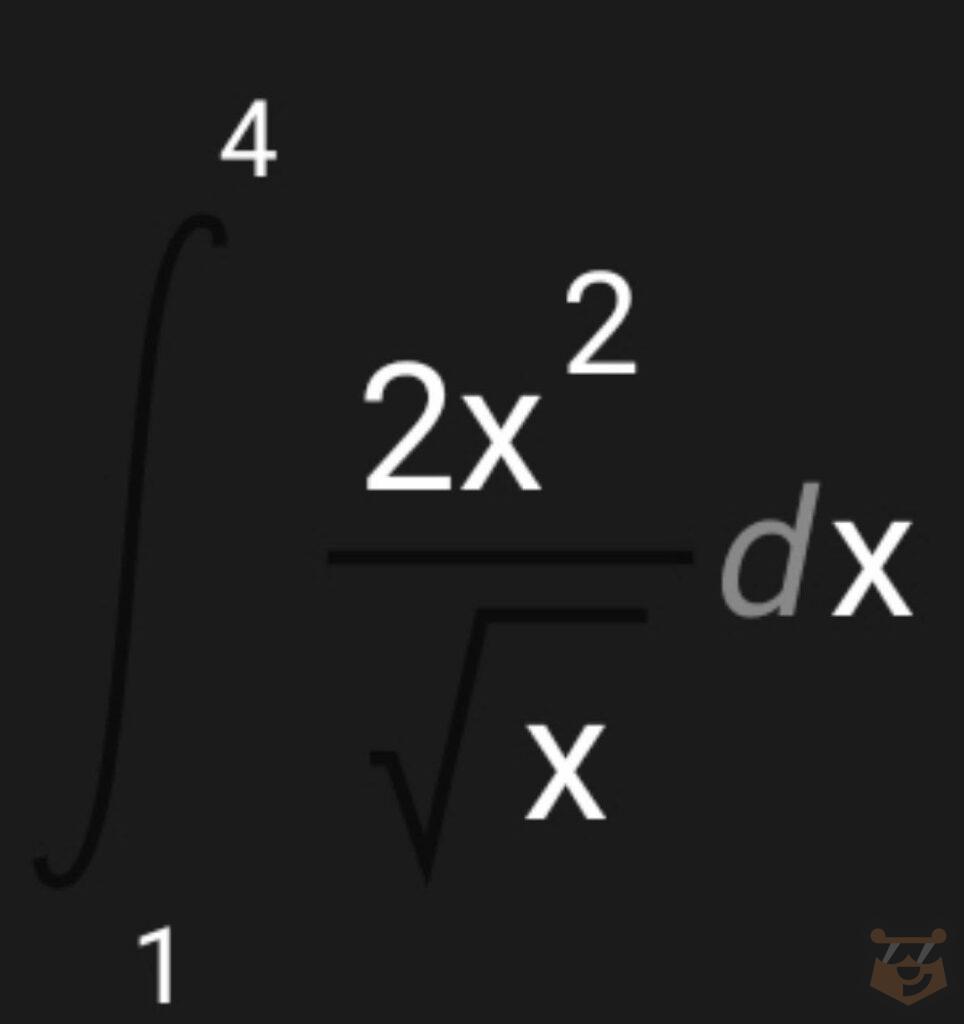
Задание№2.
Чему равна площадь фигуры ограниченной параболами у=-х^2+8 и у=х^2?
Задание№3.
Найдите объем тела вращения, ограниченного линиями у=7 и у=х^2 + 3?
Ответы: 1 — 124/5, 2 — 64/3, 3 — 576/5.
