Неопределенный интеграл
Неопределенный интеграл является одним из основополагающих понятий математического анализа. Используется неопределенный интеграл в различных областях, таких как физика, инженерные расчеты, экономика и другие науки. Следует отметить, что неопределенный интеграл тесно связан с понятиями производной и первообразной. Поэтому перед изучением интегралов необходимо освежить в памяти, что такое производная и изучить суть первообразной.

Первообразной для данной нам функции будет такая функция, производная которой равна нашей функции.
Может показаться, что это сплошная тавтология. Поэтому представим это по-другому:
Исходная функция — f(x).
Первообразная этой функции — F(x).
И тогда связь между ними выражается следующим выражением: F(x)’=f(x).
То есть первообразная это противоположное (обратное) действие производной. Это как «+» и «-», «×» и «÷». Запомним это с помощью ассоциации с любимой игрой детства у многих.
| Производная | Первообразная |
 |  |
| f(x) |  |
| F(x) |  |
Для того чтобы найти первообразную, нам необходимо запомнить определенные табличные значения.
Таблица первообразных.
| Функция f(x). | Первообразная F(x). |
| k | kx+C |
| x^n | x^(n+1)/n+1 |
| 1/x | ln|x| |
| e^x | e^x |
| a^x | ax/lna |
| sinx | -cosx |
| cosx | sinx |
| 1/sin^2x | -ctgx |
| 1/cos^2x | tgx |
С первообразной разобрались, можно приступить к неопределенному интегралу.
Неопределенный интеграл от функции f(x) это множество всех возможных первообразных для нашей функции.
Формула отражающая это выглядит так: ∫ f(x)dx= F(x) + C.
Разберём данную запись на составляющие.
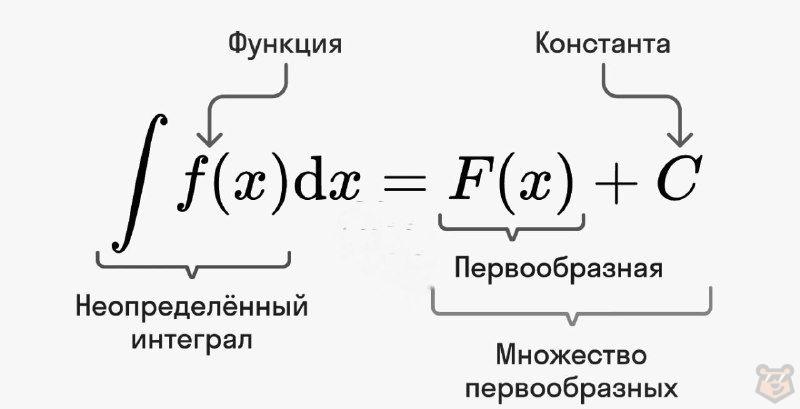
Делаем вывод, что записывать сам неопределенный интеграл принято таким образом: ∫ f(x)dx.
Также понимаем, что для вычисления будем использовать почти точно такую же таблицу, как и для первообразных.
Таблица интегралов.
| Функция f(x). | Интеграл ∫ f(x)dx. |
| k | kx+C |
| x^n | x^(n+1)/n+1 + C |
| 1/x | ln|x| + C |
| e^x | e^x + C |
| a^x | ax/lna + C |
| sinx | -cosx + C |
| cosx | sinx + C |
| 1/sin^2x | -ctgx + C |
| 1/cos^2x | tgx + C |
В общем вся эта ситуация со стороны жутко напоминает всем хорошо знакомый мем:

| Первообразная F(x). | Неопределенный интеграл ∫ f(x)dx. |
 |  |
Следующую шпаргалку поймут только избранные.

Свойство интегралов.
Также необходимо запомнить несколько свойств интегралов для того, чтобы мы могли легче их вычислять.
1) ∫ (f(x) + g(x))dx = ∫ f(x)dx + ∫ g(x)dx
2) ∫ (f(x) — g(x))dx = ∫ f(x)dx — ∫ g(x)dx
3) ∫ k×f(x)dx =k× ∫ f(x)dx
Практическая часть.
Решим несколько примером для того чтобы лучше закрепить материал и научиться правильно пользоваться таблицами.
Здание №1. Чему равен ∫ 23dx ?
Решение. Данный интеграл совпадает с табличными значениями. ∫ kdx=kx + C
Подставляем наше число и делает вычисления.
∫ 23dx=23х + С
Ответ: 23х + С.
Здание №2. Найдите неопределенный интеграл ∫ 5sinxdx.
Решение. Воспользуемся одним из свойств и вынесем число 5 за интеграл:
∫ k×f(x)dx =k× ∫ f(x)dx.
И вот теперь можем использовать таблицу.
∫ sinxx=-cosх + С
И тогда выходит, что ∫ 5sinxdx=5×∫ sinxdx=5×∫ соsx=5cosx.
Ответ: 5cosx.
Здание №3. Чему равен интеграл ∫ (8x^3+2х-10)dx ?
Решение. Вспоминаем, что ∫ (f(x) ± g(x))dx = ∫ f(x)dx ± ∫ g(x)dx. И тогда получаем, что ∫ (8x^3+2х-10)dx=∫ 8x^3dx +∫ 2хdx -∫ 10dx.
Обратимся к нашим табличным значениям.
1. ∫ 8x^3dx=8х^(3+1)/3+1=8х^4/4=2х^4 + С
2. ∫ 2хdx=2х^(1+1)/1+1=2х^2/2=х^2 + С
3. ∫ 10dx=10х + С
∫ 8x^3dx +∫ 2хdx -∫ 10dx=2х^4 + х^210х + С.
Ответ: 2х^4 + х^210х + С.
Задания по данному разделу, которые встречаются на ЕНТ.
Задачи с неопределенными интегралами на едином национальном тестировании встречаются только в профильной математике.
Задание №1. Вычислите ∫ (9х^2 + 6х^5 — 3+ 3/х) dx
Решение. Разделим наш интеграл на несколько компонентов:
∫ (9х^2 + 6х^5 — 3+ 3/х) dx= ∫ (9х^2)dx + ∫ (6х^5)dx — ∫ 3dx + ∫ (3/х)dx.
Решаем каждый интеграл отдельно, используя таблицу и свойства интегралов
1) ∫ (9х^2)dx = 9х^(2+1)/(2+1)=9х^3/3=3х^3 + С
2) ∫ (6х^5)dx = 6х^(5+1)/(5+1)= 6х^6/6=х^6 + С
3)∫ 3dx = 3х + С
4) ∫ (3/х)dx.
Воспользуемся свойством ∫ k×f(x)dx =k× ∫ f(x)dx для того, чтобы упростить себе задачу.
∫ (3/х)dx= 3×∫ (1/х)dx= 3 × lnlxl + C
5) ∫ (9х^2)dx + ∫ (6х^5)dx — ∫ 3dx + ∫ (3/х)dx = 3х^3 + х^6 + 3х + 3 × lnlxl + C
Ответ: 3х^3 + х^6 + 3х + 3 × lnlxl + C
Здание №2. Найдите чему равен интеграл ∫ (а/х + а^2/х^2 + а^3/х^3) dx.
Решение. Для начала пользуясь свойствами, разложим наш один большой интеграл на три маленьких.
∫ (а/х + а^2/х^2 + а^3/х^3) dx = ∫ (а/х)dx + ∫ (а^2/х^2)dx + ∫ (а^3/х^3)dx.
Теперь в каждом случае за интеграл вынесем числитель.
∫ (а/х)dx + ∫ (а^2/х^2)dx + ∫ (а^3/х^3)dx = а × ∫ (1/х)dx + а^2 × ∫ 1/х^2)dx + а^3 × ∫ (1/х^3)dx .
1) а × ∫ (1/х)dx.
Пример по типу ∫ (1/х)dx есть в таблице. ∫ (1/х)dx= ln lxl + C
Тогда выходит: а × ∫ (1/х)dx = аln lxl + C.
2) а^2 × ∫ 1/х^2)dx.
Представим 1/х^2=х^(-2). Получим, а^2 × ∫ х^(-2)dx.
Взглянем на таблицу и увидим, что ∫ x^ndx=
x^(n+1)/n+1 + C.
∫ х^(-2)dx = х^(-2+1)/-2+1=х^(-1)/-1=-1/х + С
а^2 × ∫ х^(-2)dx = а^2 × (-1/х)=-а^2/х +С
3) а^3 × ∫ (1/х^3)dx.
Представим 1/х^3=х^(-3). Получим, а^3 × ∫ х^(-3)dx.
Используя вышеприведенную формулу делаем вычисления.
∫ х^(-3)dx=х^(-3+1)/-3+1=х^(-2)/-2=-1/2х^2
а^3 × ∫ (1/х^3)dx= а^3 × (-1/2х^2)= -а^3/2х^2 + С
4) ∫ (а/х + а^2/х^2 + а^3/х^3) dx = а×ln lxl -а^2/х -а^3/2х^2 + С
Ответ: а×ln lxl — а^2/х — а^3/2х^2 + С.
Здание №3. Решите ∫ ((√х-2³√х+1)/⁴√х)dx.
Решение. Представим наш интеграл следующим образом: ∫ ((√х-2³√х+1)/⁴√х)dx= ∫ ((√х/⁴√(х^2)) -(2³√х/⁴√х)+(1/⁴√х))dx.
Используя свойства интеграла, получим
∫ ((√х/⁴√х) -(2³√(х^2)/⁴√х)+(1/⁴√х))dx = ∫ (√х/⁴√х)dx — ∫ (2³√х/⁴√х)dx + ∫ (1/⁴√х)dx.
1) ∫ (√х/⁴√х)dx.
Распишем √х как х^(1/2), а ⁴√х как х^(1/4)
Тогда выходит, что √х/⁴√х=х^(1/2)/х^(1/4)=х^(1/2-1/4)=х^(1/4)
∫ (√х/⁴√х)dx= ∫ х^(1/4)dx
Вспомним, что x^(n+1)/n+1 + C. Значит ∫ х^(1/4)dx = х^(1/4+1)/(1/4+1)= х^(5/4)/(5/4)= 4×х^(5/4)/5=4×⁴√х^5/5 =4×⁴√х/5 + С
2) ∫ (2³√(х^2)/⁴√х)dx.
Опять представим ⁴√х как х^(1/4) , а ³√х как х^(1/3).
2³√х/⁴√(х^2)=2×х^(2/3)/х^(1/4)=2х^(2/3-1/4)=2х^(8/12-3/12)=2х^(5/12)
∫ (2³√(х^2)/⁴√х)dx= ∫ 2х^(5/12)dx= 2× ∫ х^(5/12)dx=2×х^(5/12+1)/(5/12+1)=2×х^(17/12)/17/12=2×12×х^(17/12)/17 = 24×¹²√(х^17)/17 = 24×¹²√(х^5)/17+С
3) ∫ (1/⁴√х)dx.
Вновь распишем ⁴√х как х^(1/4), выйдет 1/⁴√х=1/х^(1/4)=х^(-1/4)
∫ (1/⁴√х)dx = ∫ х^(-1/4)dх= х^(-1/4+1)/(-1/4+1)= х^(3/4)/(3/4)=4×х^(3/4)/3=4×⁴√(х^3)/3 + С
4) ∫ (√х/⁴√х)dx — ∫ (2³√х/⁴√х)dx + ∫ (1/⁴√х)dx = 4×⁴√х/5 + 24×¹²√(х^5)/17 + 4×⁴√(х^3)/3 + С.
Ответ: 4×⁴√х/5 + 24×¹²√(х^5)/17 + 4×⁴√(х^3)/3 + С.
Задания для самопроверки:
Задание№1.
Вычислите ∫ (3соsx-15sinx)dx.
Задание№2.
Найдите ∫ (4х^3 — (1/х) + √х)dx.
Задание№3.
Чему равен интеграл ∫ ((4х — х^2 +1)/3) + √х)dx ?
Ответы: 1 — 3sinx+15cosx + C, 2 — х^4- lnlxl + 2√(x^3) + C, 3 — 2х^3/3 + х^3/9 + х/3 + С.
