Функция и ее свойства
Функция – это мощный инструмент для анализа и моделирования данных. Поэтому она является одной из важнейших концепций в математике и информатике, а также в других науках.
Функции обладают множеством свойств и особенностей. Их можно разделить на виды, каждому из которых соответствует свой неповторимый график. Разобраться во всем этом, на первый взгляд, может быть трудно. Но это необходимо сделать. Потому что понимание функций и их свойств является важной составляющей не только для успешной работы в сфере аналитики, исследований и разработок, но и конечно же, для удачной сдачи ЕНТ. Поэтому давайте “познакомимся” с самим определением функции, а также с её основными характеристиками.
Функция —
это тип отношений между двумя множествами, в котором каждому элементу из первого множества соответствует ровно один элемент из второго множества.

Если же объяснить более простым языком, то функция — это зависимость переменной у от переменной х.
То есть когда мы изменяем значение х, у нас изменяется и значение у согласно данному нам закону f(x).
Таким образом:
х — независимая величина, по-другому ее называют аргументом функции.
у — зависимая переменная, ее еще принято называть значением функции.
Это можно легко запомнить благодаря вот такой вот незамысловатой шпаргалке:

Теперь давайте для того, чтобы до конца разобраться в этом, рассмотрим несколько примеров.
Пример №1. Нам дана функция y=х.
*Также функцию можно записать и следующим образом: f(x)=х.
Предлагаю сейчас вместо х подставить 0, 1, 2, а после найти значение у.
1) При х=0, у=0
Мы можем запасать это и чуть иначе: f(0)=1
2) При х=1, у=1
Т.е. f(1)=3
3) При х=2, у=2
f(2)=5
Сделаем небольшую табличку:
| х | 0 | 1 | 2 |
| у | 0 | 1 | 2 |
Пример №2. Функция задана законом f(х)=2x+1.
Предлагаю опять вместо х подставить 0, 1, 2, а после определить значение у.
1) При х=0, у=2×0+1 у=1
f(0)=1
2) При х=1, у=2×1+1 и у=3
f(1)=3
3) При х=2, у=2×2+1 и у=5
f(2)=5
Сделаем небольшую табличку:
| х | 0 | 1 | 2 |
| у | 1 | 3 | 5 |
Пример №3. Дана функция y=x-3.
Вновь на место х ставим 0, 1, 2, а затем вычислим у.
1) При х=0, у=0-3 у=-3
f(0)=-3
2) При х=1, у=1-3 у=-2
f(1)=-2
3) При х=3, у=3-3 у=0
f(2)=0
Составим очередную таблицу:
| х | 0 | 1 | 2 |
| у | -3 | -2 | 0 |
Внимательно выполняя наши вычисления, мы убедились, что у действительно зависит от х, и вместе с ним меняет свое значение согласно тому закону, которым задана сама функция. А смотря на таблицы, мы удостоверились, что каждому х соответствует только один у.
Свойства функций
1) Область определения функции
Для того, чтобы сразу понять о чем идет речь, рассмотрим 2 примера.
Пример №1. Есть функция у=4/х.
Вместо х в данном случае мы можем подставить 1, 2, 3 и так до бесконечности. Но подставить ноль мы “не имеем права”. Ведь тогда наша функция не будет иметь смысла, так как законы математики гласят: нельзя делить на ноль.
Пример №2. Дана функция у=2/х+2.
Понимаем, что х не может быть равным -2. Потому что иначе у нас знаменатель дроби вновь будет являться нулем, а как мы говорили выше, это противоречит здравому смыслу в математике.
Теперь мы знаем, что мы не можем на место х поставить абсолютно любые числа, существуют ограничения.
Допустимые значения аргумента, при которых функция имеет смысл, и называют областью определения.
Она обозначается так: D(y).
Как сделать правильную запись для конкретной функции ? Разберем с помощью тех же двух примеров.
Пример №1. х≠0 D(y)=(-∞;0) U (0;+∞)
Пример №2. х≠-2 D(y)=(-∞;-2) U (-2;+∞)
Главное, что нужно понять, так это то, что область определения каждой функции будет зависеть только от самой функции и может быть ограниченной или бесконечной.
2) Множество значений функции
Это такие значения, которые принимает у (то есть наша функция), при допустимых значениях х.
В письменных работах множество значений обозначаем следующим образом: Е(y).
Вас могла посетить мысль, что значения переменной у не ограничены по сравнению с переменной х. Но такое предположение будет ошибочным. Для того, чтобы в этом убедиться, давайте обратимся к одной функции.
у=х^2
Предлагаю вам поставить на место величины х для начало -1 и 1, а потом 2 и -2.
- При х=1, у=1^2 и у=1
- При х=1, у=(-1)^2 и у=1
- При х=1, у=2^2 и у=4
- При х=1, у=(-2)^2 и у=4
Как вы заметили, какой бы аргумент мы не выбрали, наша функция не принимает отрицательные значения. Ведь любое число во второй степени будет являться положительным.
Таким образом, в данном случае Е(y)=(0;+∞).
И выходит, что у значений величины у тоже существуют свои границы, и зависят они так же лишь от самой функции.
3) Нули функции
Нулями функции будут значения аргумента (х), при которых функция равна нулю.
Для того, чтобы лучше понять данное свойство, вновь обратимся к нескольким примерам.
Пример №1. Дана функция у=х^2-9.
Найдем нули функции подставив вместо у 0. Получим уравнение:
х^2-9=0.
Теперь надо его решить.
х^2=9.
х1=3
х2=-3
Найденные корни уравнения и будут являться нулями этой функции.
Пример №2. Функция задана законом f(х)=4x+8.
Принцип точно такой же.
1) 4x+8=0
2) 4x=-8
3) х=-8/4
4) х=-2
4) Промежутки знакопостоянства
Это множество значений аргумента, при которых значение функции (т.е. наша переменная у) бывает только положительной или только отрицательной. Это свойство также важно при работе с графиками функции.
Вернемся к функции, которую уже разобрали до этого: у=х^2.
Вспомним,что при любом аргументе, наша функция не принимает отрицательные значения. И получается, что значение функции положительно при х∈(-∞;+∞).
Рассмотрим еще один пример. y=x-5
Для того, чтобы найти где функция принимает отрицательные значения, составим неравенство, в котором наша функция меньше нуля:
x-5<0
x<5
То есть, наша переменная у будет с минусом когда х∈(-∞;5)
Теперь найдем значения функции с плюсом. Для этого сделаем неравенство, где функция больше нуля:
x-5>0
x>5
Выходит, у функции будут положительные значение при х∈(5;+∞).
5) Монотонность функции
Это такие интервалы, где функция либо возрастает, либо убывает. Чтобы их найти обратимся к определениям.
1) Функция возрастает на том промежутке, где большему значению переменной х из этого промежутка соответствует большее значение переменной у.
2) Функция убывает на том промежутке, где большему значению переменной х соответствует меньшее значение переменной у.
Звучит на самом деле ужасно. Поэтому давайте распишем это более простым языком (да простят нас гурманы математики.)
1) Функция возрастает на интервале оси Ох, где ее график «поднимается» слева направо.
2)Функция убывает на интервале оси Ох, где ее график «падает» слева направо.
Уже полегче, но чтоб уж точно все укладывалось в голове, обратимся к графику одной функции.
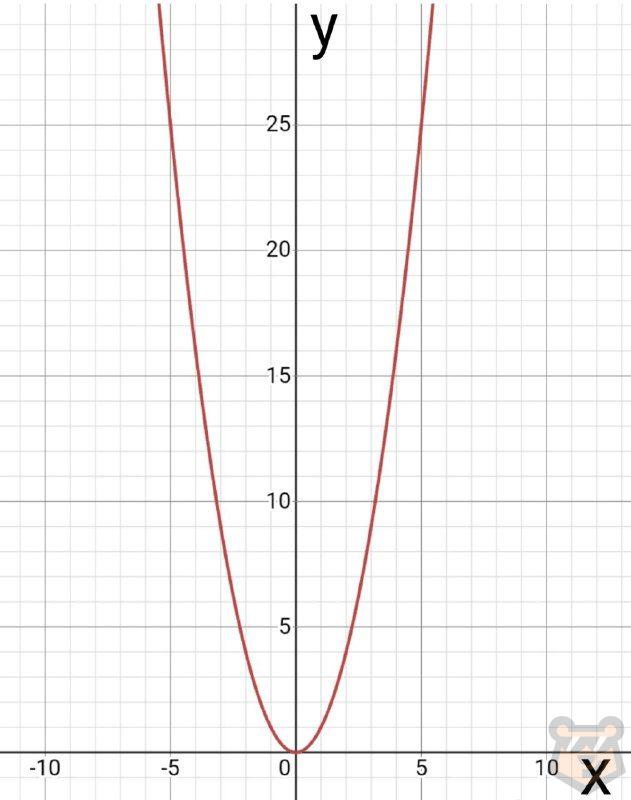
Хорошо присмотримся к оси абсцисс (х) и постараемся найти, где график падает слева направо, а где он в том же направлении растет.
График падает на промежутке (-∞;0).
График поднимается на промежутке (0;+∞).
Получается, что наша функция на интервале (0;+∞) возрастает, а на интервале (-∞;0) она убывает.
Существует еще один способ для того, чтобы найти промежутки монотонности, но прежде чем им воспользоваться, необходимо изучить что такое «производная».
6) Периодичность функции
Периодические функции — это те функции, которые через определенный промежуток (период) визуально на графике повторяются.
Для наглядности рассмотрим один график:
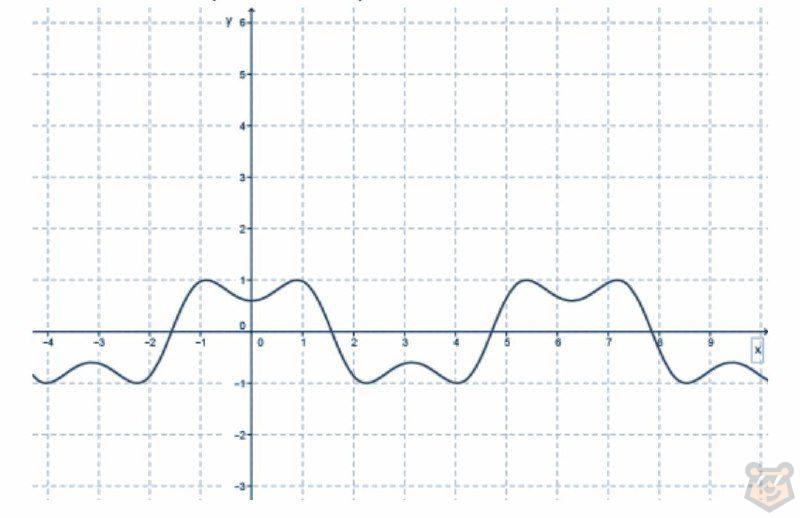
Смотря на иллюстрацию, легко заметить, что функция через определенный период действительно повторятся.
С понятием «периодичность функции» вы поближе познакомитесь, при изучении тригонометрических функций.
7) Четность/нечетность функции
Функция будет являться четной только тогда, когда для любого х из ее области определения выполняется следующее равенство: f(-x)=f(x).
Функцию будем называть нечетной в том случае, когда для любого х из ее области определения выполняется равенство: f(-x)= -f(x).
Иначе говоря, четная функция — это та функция, у которой значение не меняется после изменения знака аргумента.
А нечетная функция — это функция, у которой значение меняется после изменения знака аргумента.
Чтобы это лучше понять, разберем несколько функций.
Пример №1. Дана функция у=х^4.
Подставим вместо х сначала 1, а потом -1.
1) При х=1 , у=1^4 и у=1
2) При х=-1, у=(-1)^4 и у=1
Получается, что f(-1)=f(1).
Сравним наш результат с равенствами и убедимся в том, что функция у=х^4 является четной.
Пример №2. Задана функция у=х^3.
Вновь подставим вместо х 1, а затем -1.
1) При х=1 , у=1^3 и у=1
2) При х=-1, у=(-1)^3 и у=-1
Получаем: f(-1)=-f(1).
Сравниваем с равенствами и понимаем в том, что функция у=х^3 является нечетной.
Запомним это с помощью небольшой шпаргалки.
| у в нечетной функции. | у в четной функции. |
 |  |
Практическая часть.
Задание №1. Исследуйте функцию у=х^2-3х^4 на четность и на нечетность.
Решение. Подставим вместо х любое положительное число, а потом его “отрицательного близнеца”. Например, 1 и -1.
При х=1 у=1^2-3×1^4=1-3=-2
При х=-1 у=(-1)^2-3×(-1^4)=1-3=-2
При смене знака у переменной х значение переменной у не поменялось. Значит функция у=х^2-3х^4 является четной.
Ответ: функция четная.
Задание №2. Дана функция у=2х+16. Найдите промежутки знакопостоянство.
Решение. Составим два неравенства.
1) Интервал, где положительные значения функции:
2х+16>0
2х>-16
х>-16/8
х>-2
Выходит, что функция будет со знаком «+» когда х ∈ (2;+∞)
2) Интервал, где отрицательные значения функции:
2х+16<0
2х<-16
х<-16/8
х<-2.
Получается, функция будет отрицательной когда х ∈ (-∞;-2).
Ответ: х ∈ (-∞;-2) – отрицательный у. (2;+∞) – положительный у.
Задание №3. Функция задана законом f(x)=-(x+4)^2+1. Определите промежутки монотонности по графику.
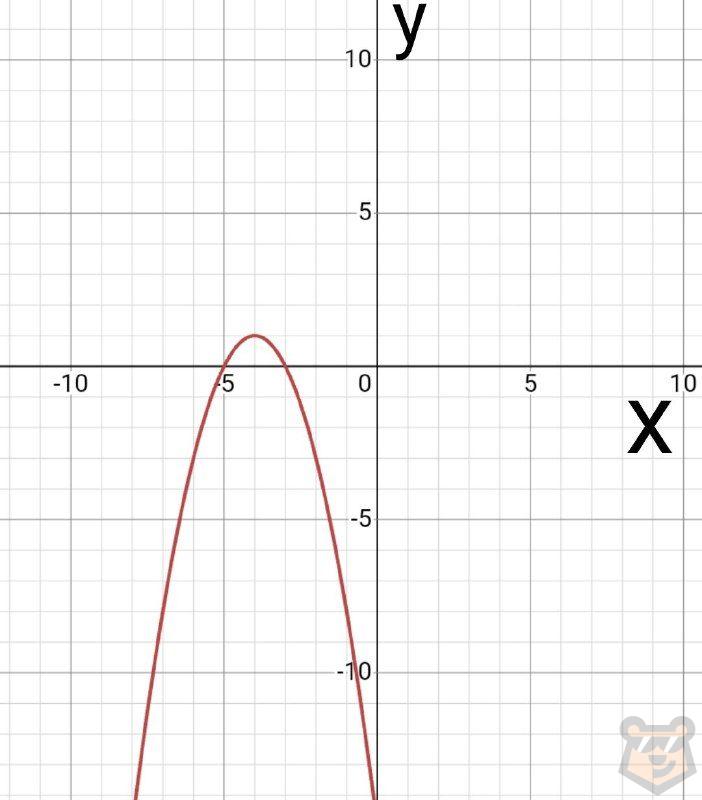
Решение. Внимательно изучаем наш график, а конкретно ось Ох. Отмечаем, что функция поднимается слева направо на промежутке (−∞;-4).
Также видим, что график падает слева направо на интервале (-4;+∞).
Ответ: функция убывает на промежутке, где x ∈ (-4;+∞), а возрастает она когда x ∈ (-∞;-4).
Задания по данному разделу, которые встречаются на ЕНТ.
Задания, связанные с основными свойствами функции, на тестировании присутствуют только в профильной математике. Давайте вместе прорешаем типы задач, которые могут вам встретиться.
Задание №1. Найдите область определения функции f(x)=√(1+3x)/x-2.
Решение. В данном случае нужно обратить внимание и на знаменатель, и на числитель дроби.
1) х-2.
Помним, что на ноль делить нельзя.
Тогда выходит, что
х-2≠0
х≠2
2) √(1+3x)
Здесь мы применим наше знание того, что нельзя вычислить квадратный корень из отрицательного числа.
Но нужно учесть, что мы можем посчитать корень из нуля.
Значит составим следующее неравенство.
√(1+3x)≥0
Теперь решим его.
2.1) Возведем обе части во вторую степень.
(√(1+3x))^2≥0^2
2.2) Получим: 1+3x≥0
2.3) Делаем оставшиеся вычисления.
3х≥-1
х≥-1/3.
3) Делаем координатную прямую.
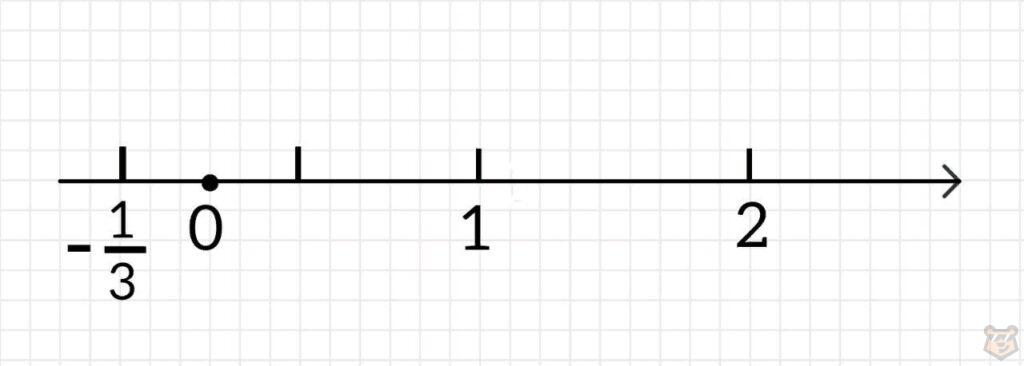
4) Отмечаем на ней не закрашенной точкой -1/3, а закрашенной точкой отмечаем 2.
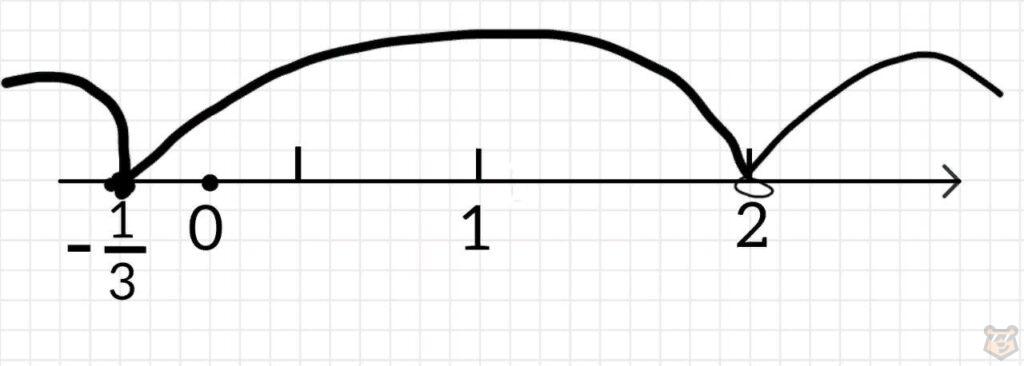
5) Интервал от минус бесконечно до -1/3 не подходит, так как у нас х≥-1/3.
Промежуток [-1/3;2) подходит потому что подходит под два наших условия. То есть входящие сюда числа не равны 2, и больше либо равны -1/3.
С интервалом (2;+∞) аналогичная история, он подходит под наши два критерия.
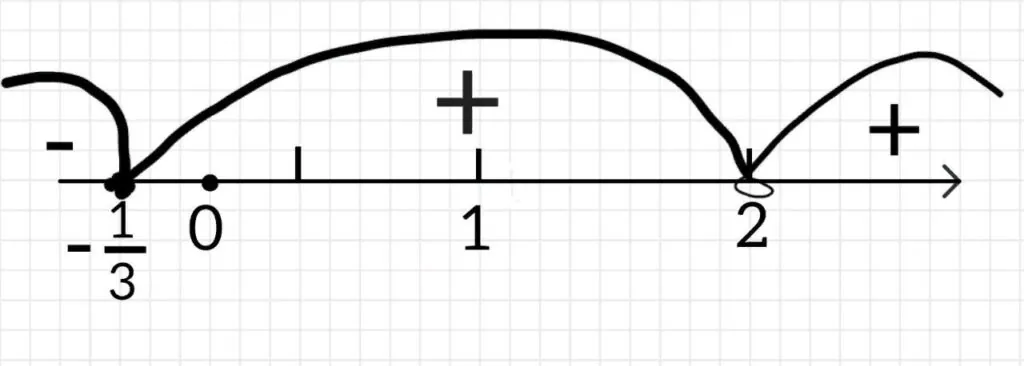
Таким образом, областью определения функции являются следующие промежутки:
(-∞;-1/3] U (2;+∞)
Ответ: D(y)=(-∞;-1/3] U (2;+∞).
Задание №2. Найдите значение выражения f(-2) + f(2), если дана функция f(х)=х^2-2х+5.
Решение. Просто подставляем -2 и 2 в нашу функцию, а потом решаем выражение.
1) При х=-2, у=(-2)^2-2×(-2)+5=4-(-4)+5 и у=13
2) При х=2, у=(2)^2-2×(2)+5=4-4+5 и у=5
3) И тогда f(-2) + f(2)=13+5=18
Ответ: 18.
Задание №3. Укажите наибольшее и наименьшее значение функции f(x)=x^2-4x+3 на отрезке [1;4].
Решение. В этой задаче нужно всего лишь вместо х подставить числа, которые входят в данный нам промежуток, а потом среди получившихся значений найти максимальное и минимальное.
1) При х=1, у=1^2-4×1+3=1-4+3 и у=0.
2) При х=2, у=2^2-4×2+3=4-8+3 и у=-1.
3) При х=3, у=3^2-4×3+3=9-12+3 и у=0.
4) При х=4, у=4^2-4×4+3=16-16+3 и у=3.
Получается, нашим максимальным значением является 3, а минимальным будет -1.
Ответ: 3, -1.
Задание №4. Скорость тела со временем изменяется согласно закону f(x)=3x^2-2. Найдите во сколько раз скорость на 7 секунде движения больше, чем на 3.
Решение. Выходит мы ищем отношение f(7)/f(3).
f(7)=3×(7^2)-2=3×49-2=147-2=145
f(3)=3×(3^2)-2=3×9-2=27-2=25
И получается, что f(7)/f(3)=145/25=5.8
Ответ: в 5.8 раз.
Задания для самопроверки:
Задание№1.
Найдите область определения функции f(x)=√(1-3x)/x+2.
Задание№2.
Определите наименьшее и наибольшее значение функции y=2x-x^2+6 на отрезке [6;9]
Задание№3.
Дана функция у=х^2-9. Исследуйте функцию на четность и на нечетность. Найдите область определения и множество значений. Определите промежутки знакопостоянства.
Ответы:
1 — D(y)=(-∞;-2) U (-2;1/3].
2 — -18, -57.
3 — функция четная,
D(у)=(-∞;+∞),
Е(у)=[-9;+∞),
на промежутке (-3;+3) значение функции отрицательное,
на промежутках (-∞;-3) U (3;+∞) функция является положительной.
