Функции и их графики
Графики функций — это важный инструмент для визуализации математических функций. Они позволяют наглядно представить изменение значений функции в зависимости от ее аргумента. С помощью графиков можно анализировать поведение функции, находить ее нули, экстремумы, а также строить прогнозы для будущих значений. Изучение графиков функций является важным элементом при изучении математики и других научных дисциплин. Они помогают визуально представить сложные математические концепции и делают их более доступными для понимания.
Графики функций играют большую роль не только в образовании, в научных исследованиях, технических расчетах, финансовой аналитике и многих других областях, но и в подготовке к единому национальному тестированию.
Узнав что такое функция в целом и какими основными свойствами она обладает, можем смело приступать к изучению определенных видов функций и их графиков.
График функции.
График функции представляет собой набор точек, соединенных линиями или кривыми, которые отражают значения функции в определённых точках области определения.
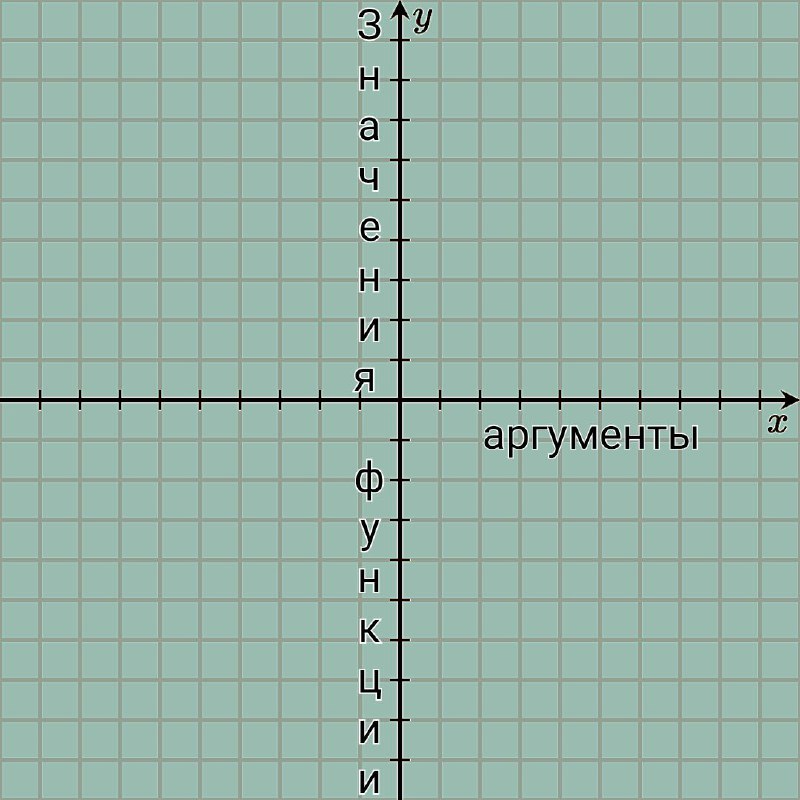
При построении графика абсциссы у нас равны аргументам, а ординаты равняются соответствующим значениям функции.
Выходит по оси Ох мы откладываем значение нашей переменной х, а по оси Оу мы отмечаем значение нашей переменной у.
Линейная функция.
Эта такая математическая функция, вид которой представлен следующим образом: f(x)=kx+b.
Мы помним, что x — это наша независимая переменная. Но чем же тогда являются другие буквы ?
k и b — это наши константы, то есть постоянные числовые значения. У каждой функции они свои и могут быть представлены как отрицательными, так и положительными числами, и даже дробями. Теперь давайте узнаем какую роль они играют в построении графика.
Сам график линейной функции при любом расклад представляет собой прямую линию.
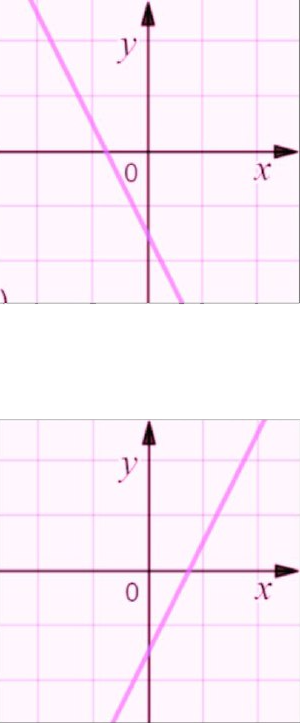
Как вы можете заметить, опираясь на представленные иллюстрации, то эта линия может быть наклонена вправо или влево, может иметь разный угол уклона. Вот тут то и проявляются наши константы.
Параметром k определяет наклон функции. Чем больше значение k, тем круче наклон прямой.
Что касаемо коэффициента b, то все без исключения прямые проходят через точку (0;b). В этой же точке график и пересекает ось Оу.
А ось Ох пересекается прямой в точке (-b/k;0).
Насчет монотонности, линейная функция всегда обладает монотонным поведением. Получается, когда k>0, то функция возрастает. Потому что если посмотреть то наш график на всей оси абсцисс (х) слева направо «поднимается».
А когда k<0, то функция убывает. Потому что если посмотреть, то наш график на всей оси Ох слева направо «падает».
| k>0 | k<0 |
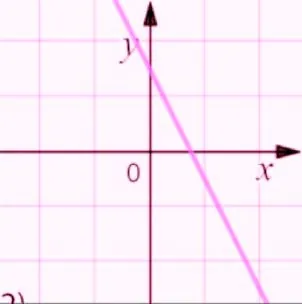 | 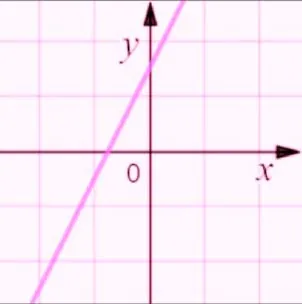 |
При k=0 график линейной функции будет параллелен оси абсцисс и станет горизонтальной прямой.
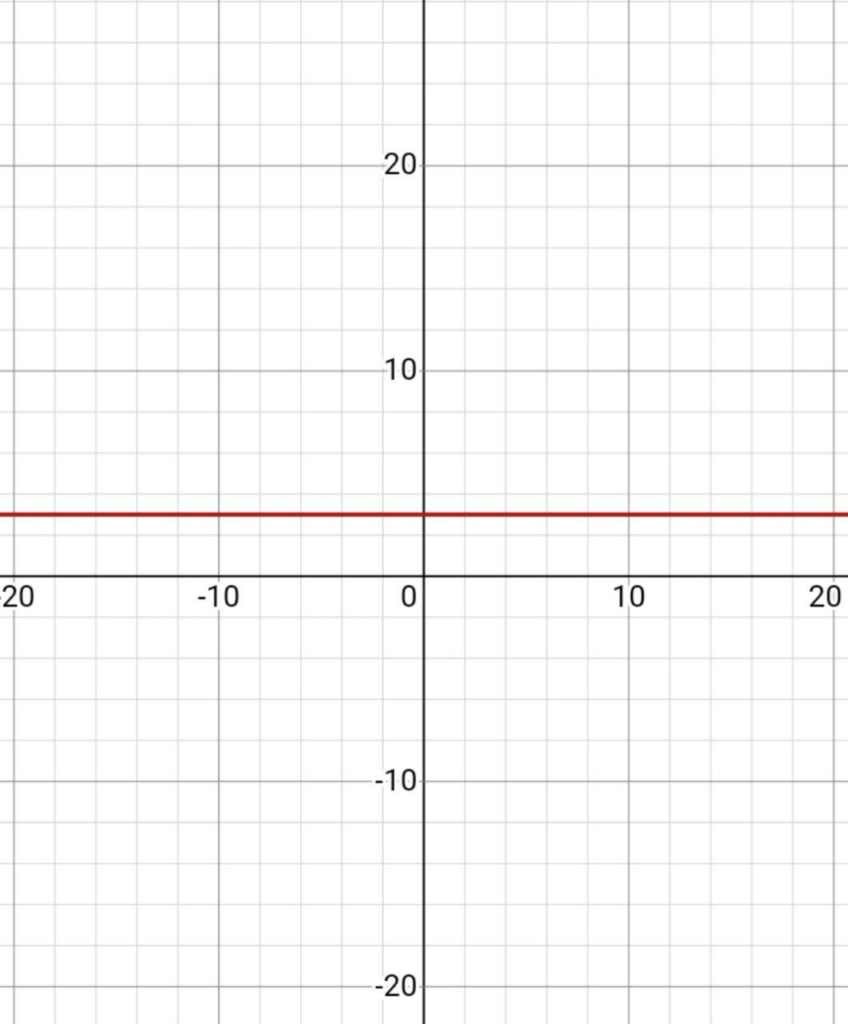
При b=0 график функции будет проходить через начало координат, а значит, функция будет пересекать оси координат в точке (0,0).

Предлагаю построить один график для того, чтобы вс усвоить. Нам дана функция f(x)=3x+1. Выходит k=3, b=1. Уж делам выводы. что функция возрастает.
Для того, чтобы визуально отразить линейную функцию нам достаточно взять две точки. Поэтому вместо х подставим 0 и 1.
1) При х=0 у=3×0+1=1 (0;1)
2) При х=1 у=3×1+1=4 (1;4)
Сделаем таблицу, чтобы не запутаться.
| х | 0 | 1 |
| у | 1 | 4 |
Теперь чертим координатную плоскость и отмечаем две наши точки: (0;1) и (1;4).
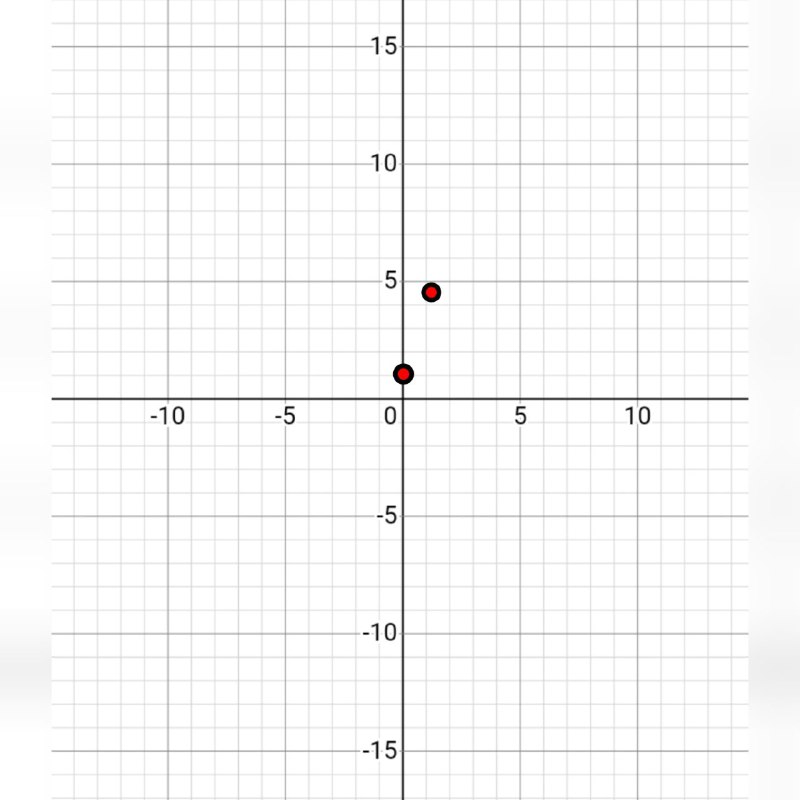
Проводим через наши точки прямую, и все, наш график готов.
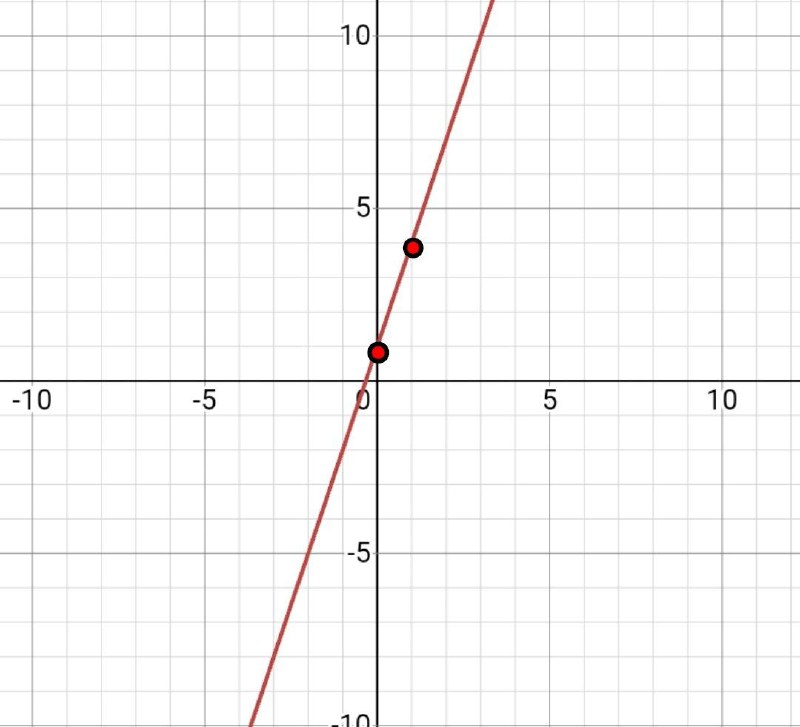
Пример №3. Функция: f(x)=x+1.
Не стоит думать, что k тут нет. Это будет ошибкой. Этот параметр тут есть просто k=1. Ведь если умножить любое число на 1, то получите то же число. Потому 1 и не пишут.
Пример №3. Дана прямая у=3х.
В данном случае b тоже никто не съел, просто b=0. Так как если мы нуль прибавим или отнимем, то ничего не изменится. Поэтому будьте внимательны.
Для закрепления всей информации разберем одну функцию полностью.
Нам дана прямая у=2х-4.
Получается, k=2 , b=-4. Наша функция возрастает.
Берем две точки 2 и 3. Подставляем в наше уравнение.
1) При х=2 у=2×2-4=0 (4;0)
2) При х=3 у=2×3-4=2 (3;2)
Чертим график.

Замечаем , что прямая действительно пересекает ось Оу в точке (0;b), то есть в нашем случае в точке (0;-4). Также видим, что пересечение с осью Ох происходит в точке (-b/k;0), для нашей функции это (2; 0)
Парабола.

Это квадратичная функция. Она имеет вид f(x)=ax^2+bx+c.
Тут у нас a, b, c тоже выступают в роли неизменных параметров.
График такой функции представляет собой параболу. Это кривая, форма которой представлена дугой.
а — старший коэффициент, причем, a ≠ 0. От того, каким числом является этот параметром (отрицательным или положительным) зависит направление ветвей нашей параболы.
Когда перед а стоит знак «+», то ветви направлены вверх, а когда перед а стоит знак «—», то вниз.
| а<0 | а>0 |
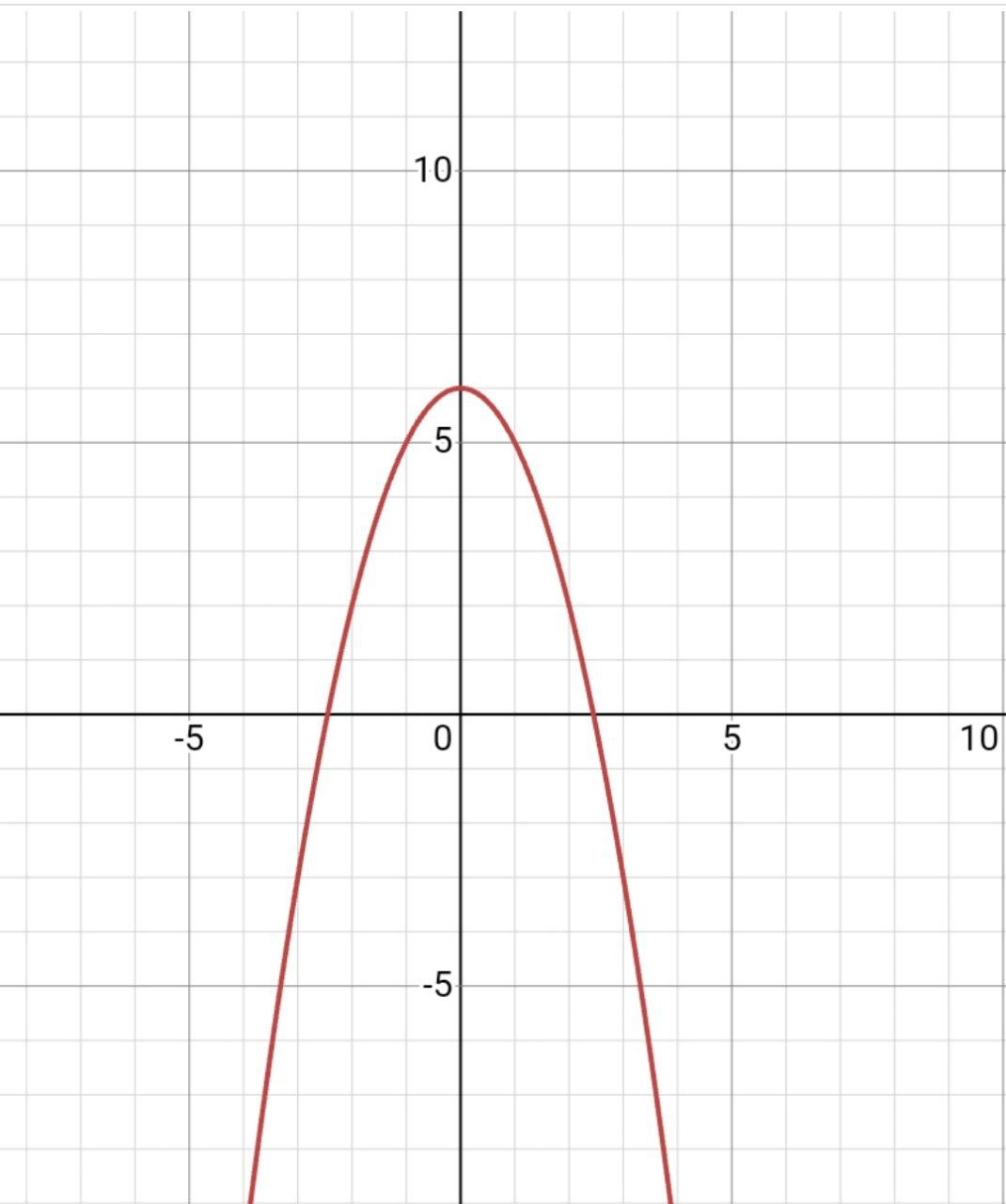 |  |
А от b и с зависит расположение вершины параболы. Она указана на графике.
То есть график квадратичной функции может сдвигаться вверх, вниз, влево или вправо путем изменения этих коэффициентов.
Если b является положительным числом, то смещение вершины параболы будет сделано влево от начала координат.
а=2, значит график делает 1 “шаг”влево. (т.е. наше смещение в 2 раза меньше b)
Если b является отрицательным числом, то смещение вершины параболы будет сделано вправо от начала координат.
а=-4, тогда гипербола уходит на 2 единицы вправо. (т.е. наше смещение в 2 раза меньше b)
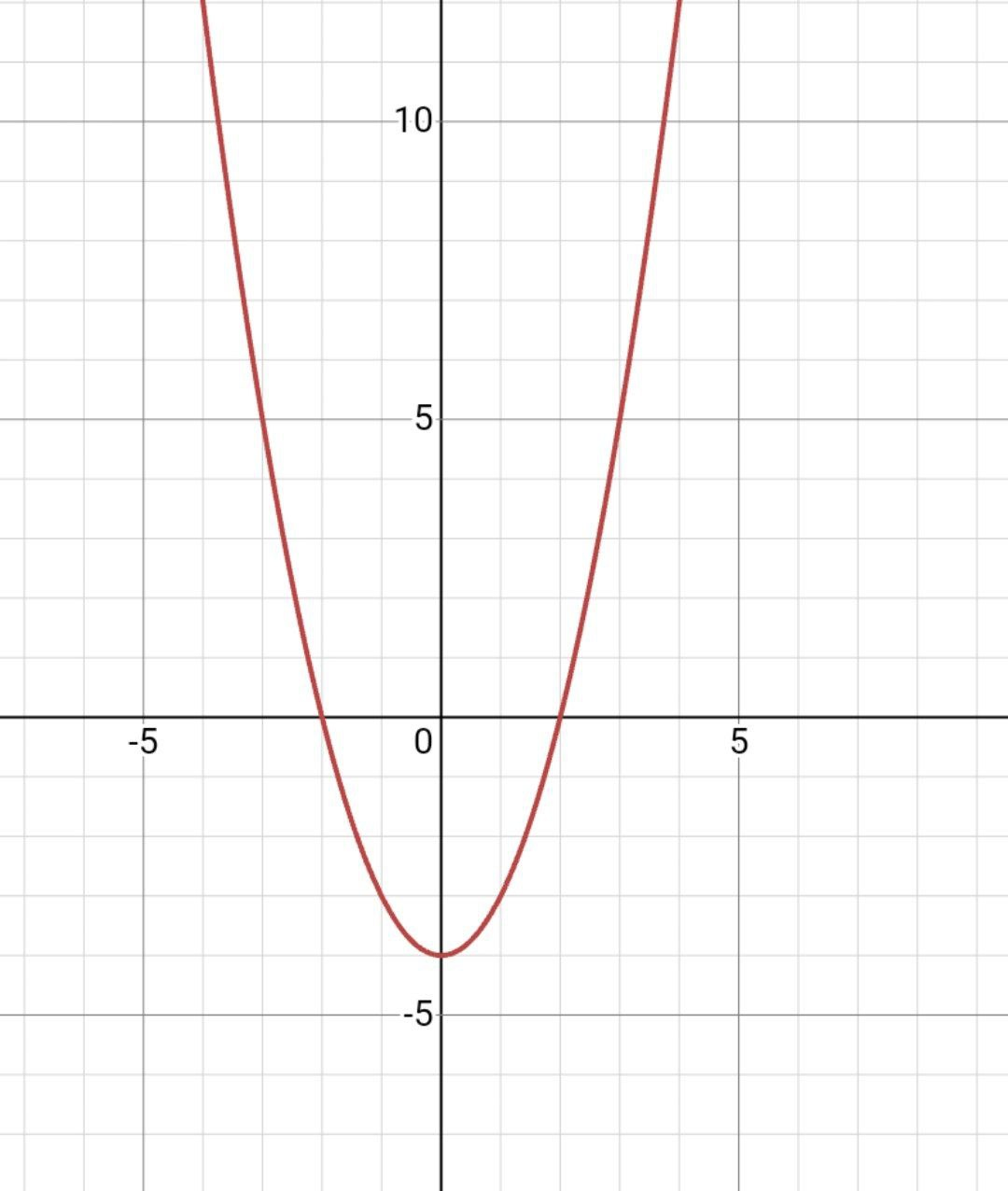
Когда с меньше нуля, то вершина параболы смещается вниз от начала координат.
с=-3, выходит график опускается на 3 ступеньки.
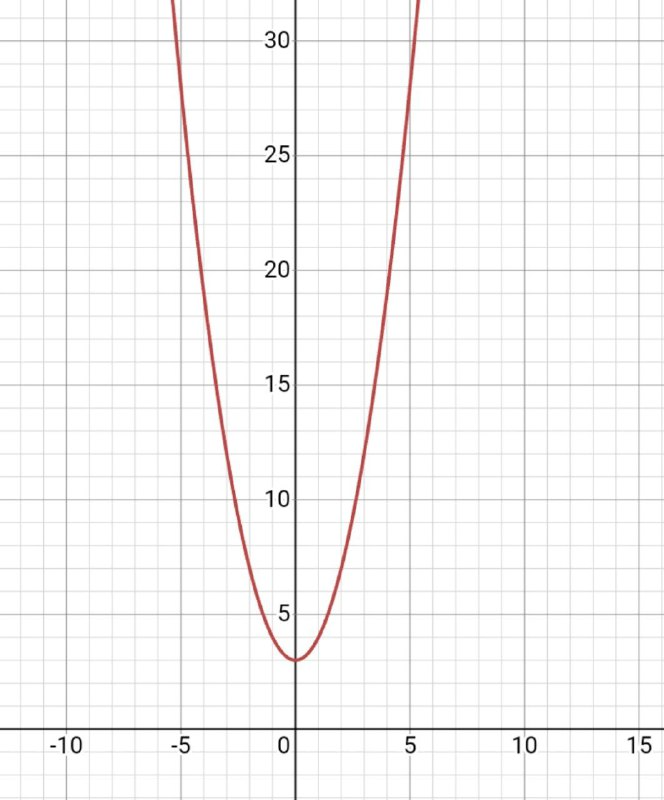
Когда с больше нуля, то вершина параболы смещается вверх от начала координат.
с=1, получается, что гипербола подниматься на 1 единицу.
| b<0 | Стандарт | b>0 |
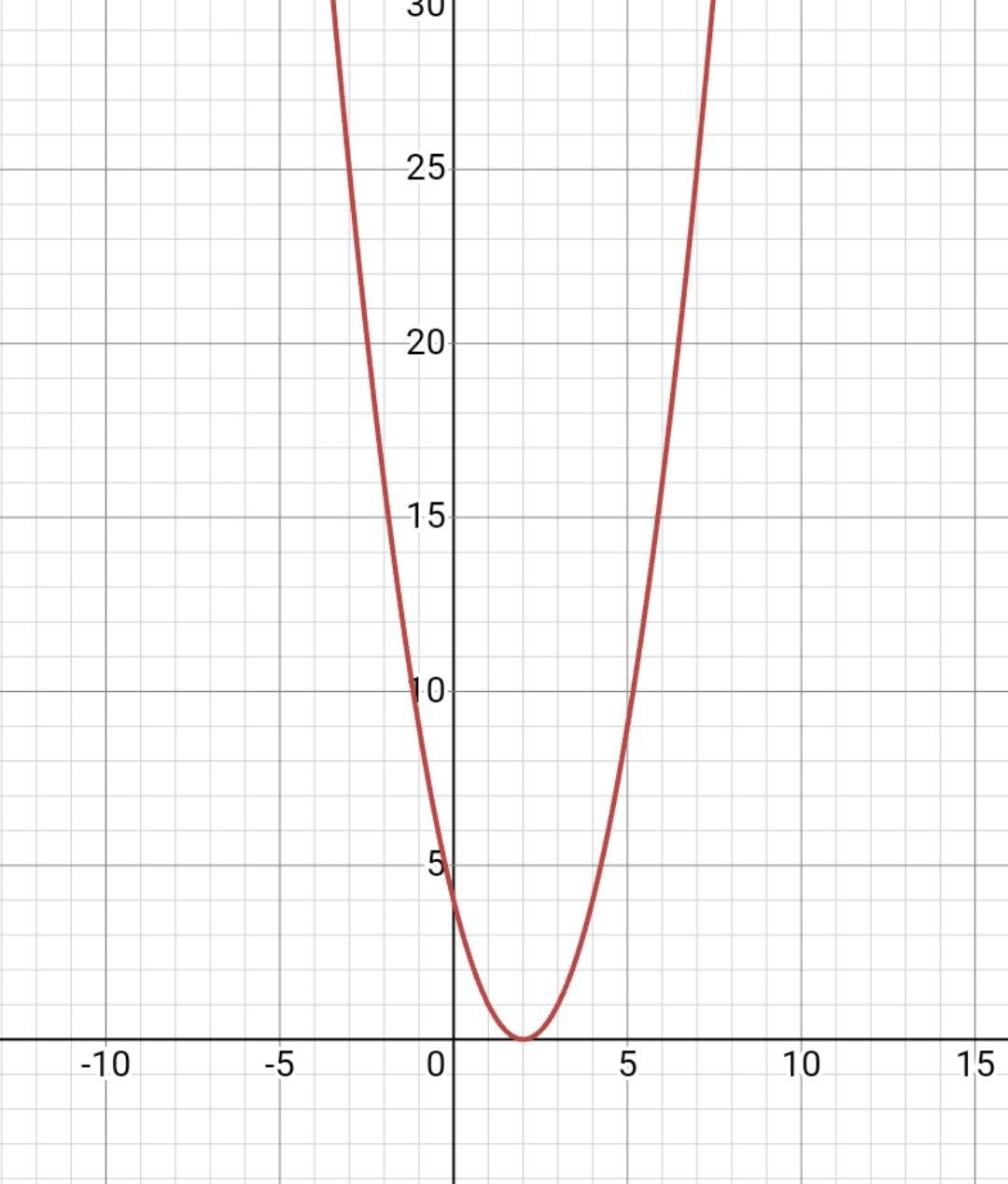 |  | 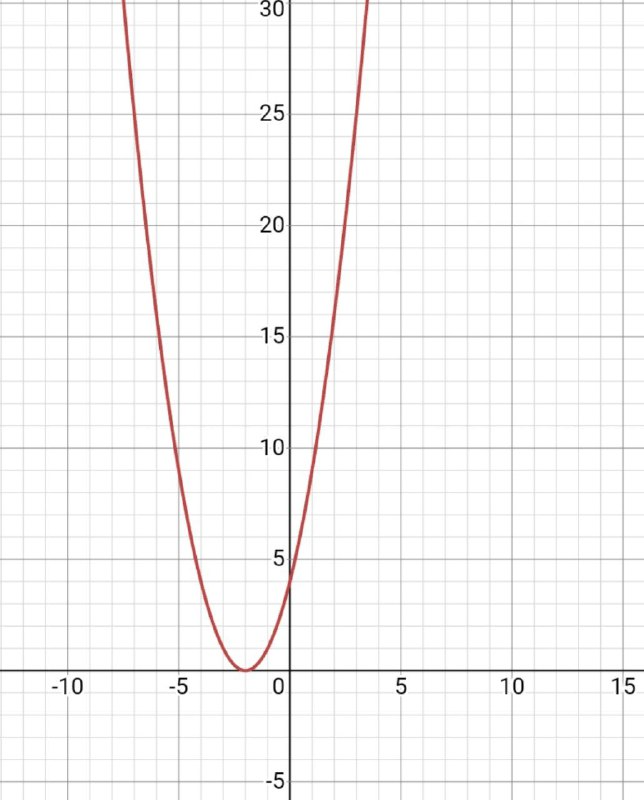 |
| c<0 | Стандарт | c>0 |
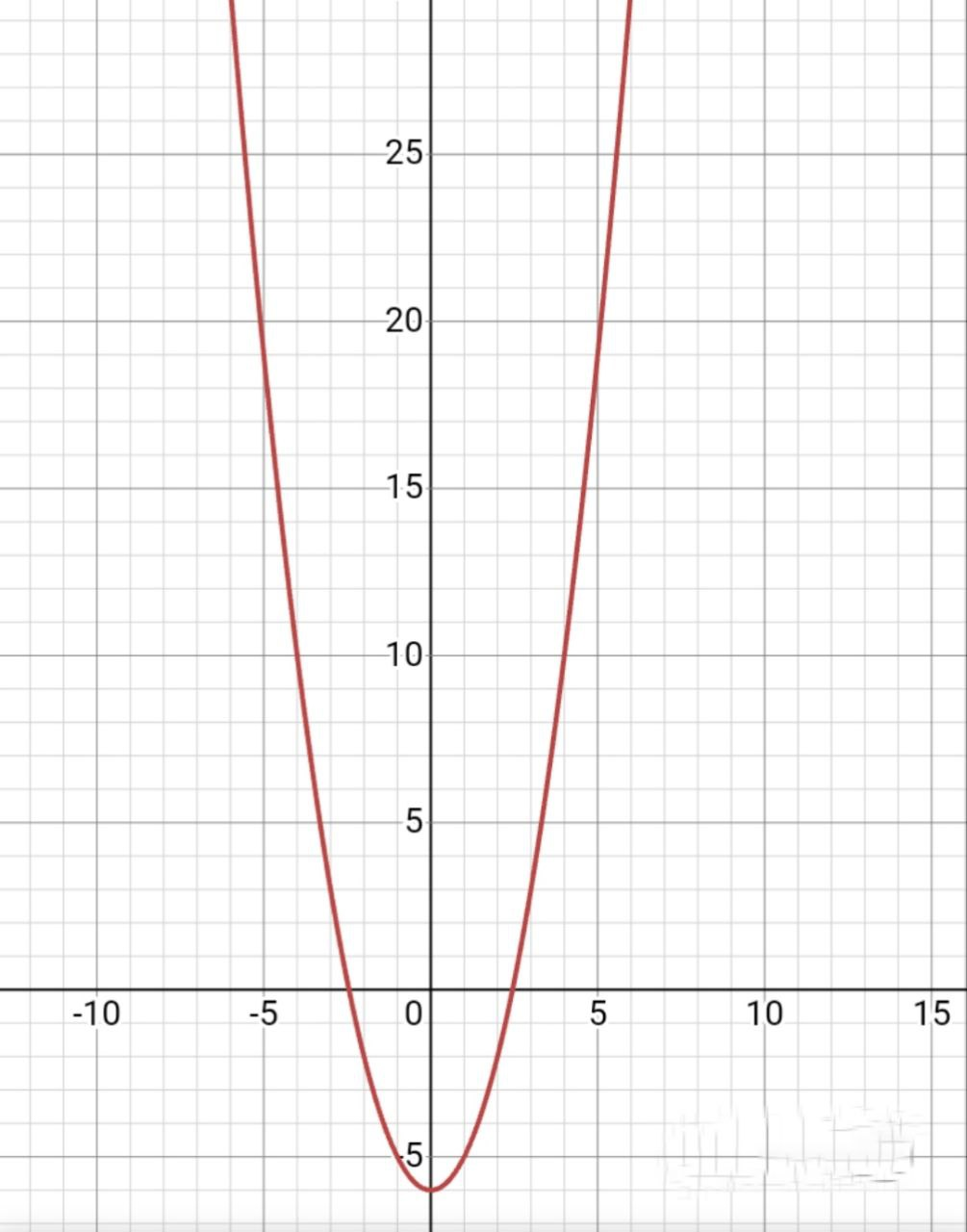 |  |  |
Для того, чтобы найти координаты вершины , которые принято обозначать как (х0; у0), мы должны воспользоваться формулой.
Необходимый аргумент будем вычислять так х0=-b/2a. А нужное значений переменной у будет являться f(x0).
Т.е. мы находим х0, а потом ищем у0, просто подставив наш аргумент в саму функцию. На примере, будет легче понять.
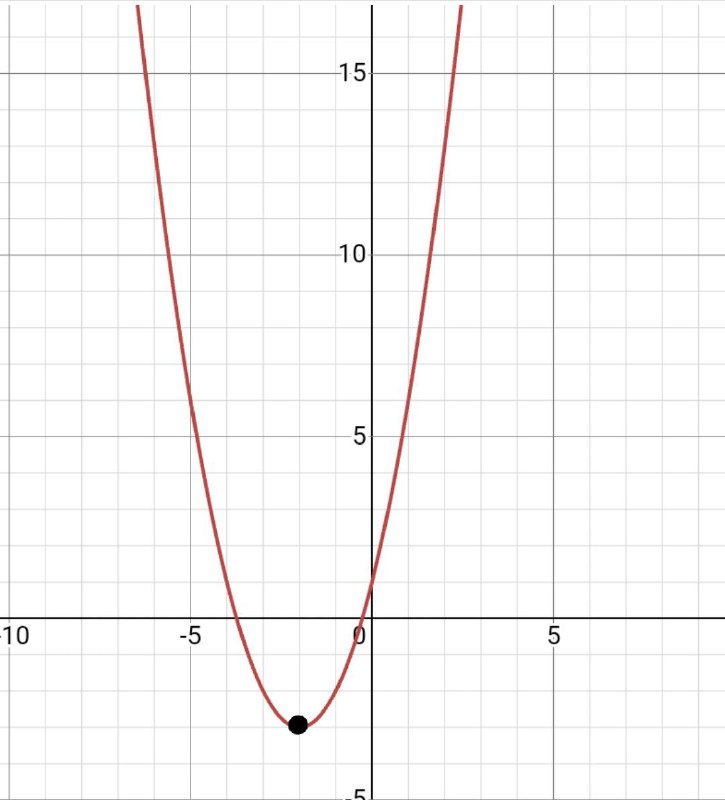
Возьмем параболу у=-2х^2+4x+1. а=-4, значит ветви параболы направлены вниз. b=2, c=1. Ищем нашу вершину.
1) х0=-(4)/2×(-2)=1
2) у0=-2×1+4×1+1=3
Получили (1;3).
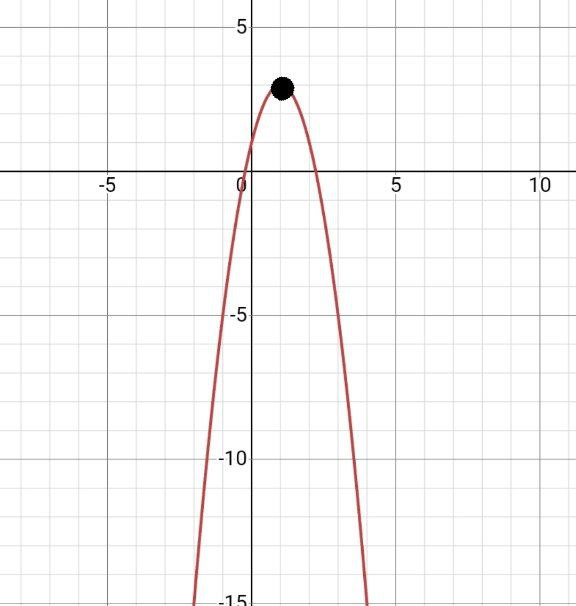
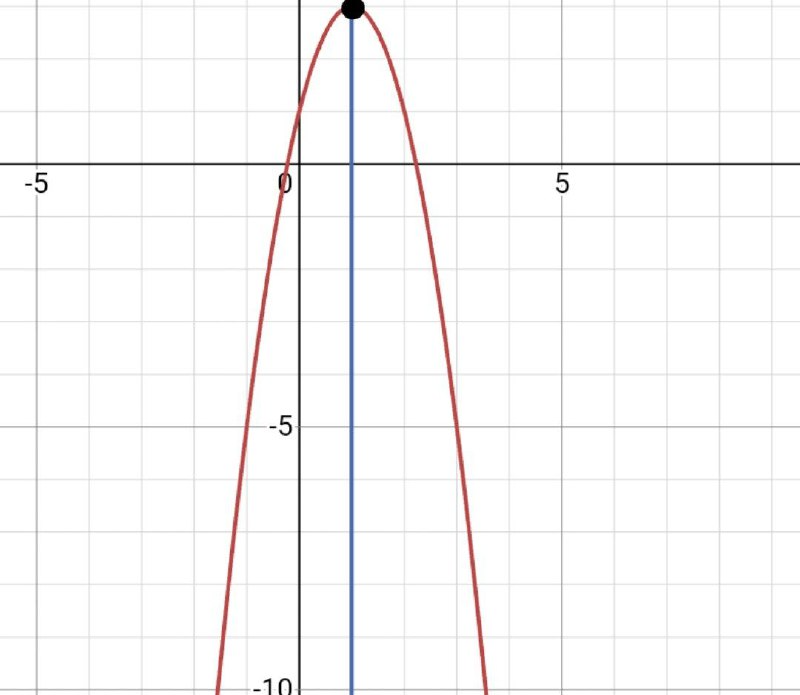
Можно заметить, что через точку х0 проходит ось симметрии в параболе. Эта прямая оформляется таким образом: х=х0. В нашем случае мы запишем х=1.
Для того, чтобы найти точку пересечения с осью Ох: мы в нашу функцию вместо у подставляем 0 и решаем уравнение.
Координатами точки, где прямая пересекаться с осью Оу являются (0;с).
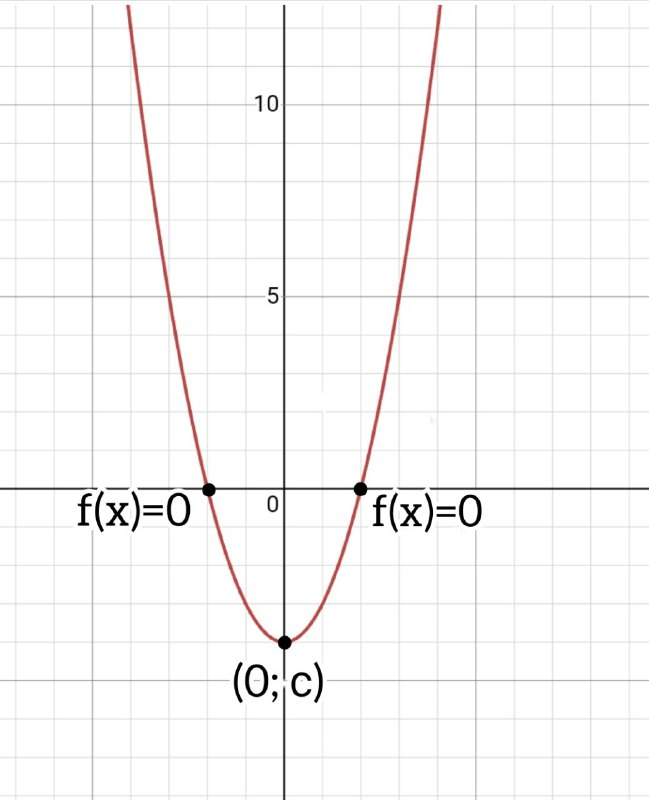
Разберемся в этом на примере у=х^2-3х+2
1) с=2, выходит (0; 2)
2) х^2-3x+2=0
2.1. D=(-3)^2-4×2×1=9-8=1=1^2
2.2. х1=-(-3)+1/2×1=4/2=2 (2; 0)
х2=-(-3)-1/2×1=2/2=1 (1; 0)
Прошу обратить внимание на то, что функция у=х^2 тоже является параболой. И а, и с, и b у нее есть. Ведь она записана потому что а=1, с=0, b=0.
Также функция вида у=(х+3)^2 будет параболой. Во-первых, как мы и сказали парабола — это квадратичная функция. А в нашей в функции есть вторая степень, так что все соответствует. А во-вторых, если мы раскроем скобки и разложим выражение по формулам сокращенного умножения, то получим у=х^2+6х+9, и тогда наша функция полностью совпадает с общим видов параболы.
Так, вершину, точки пересечения и ось симметрии мы научились находить, время учиться составлять график. Есть вариант построения, где необходимо найти сначала все перечисленное и сделать несколько махинация..
Скажите, что долго, пожалуй соглашусь.
Поэтому мой вам совет: берем 5 чисел (-2, -1, 0, 1, 2), подставляем их, вычисляем и чертим график.
Нам дана парабола у=х^2+2.
1.
1) При х=-2 у=(-2)^2+2=6 (-2;6)
2) При х=-1 у=(-1)^2+2=3 (-1;3)
3) При х=0 у=0^2+2=2 (0;2)
4) При х=1 у=1^2+2=3 (1;3)
5) При х=2 у=2^2+2=6 (2;6)
2. Чертим координатную плоскость отмечаем точки.
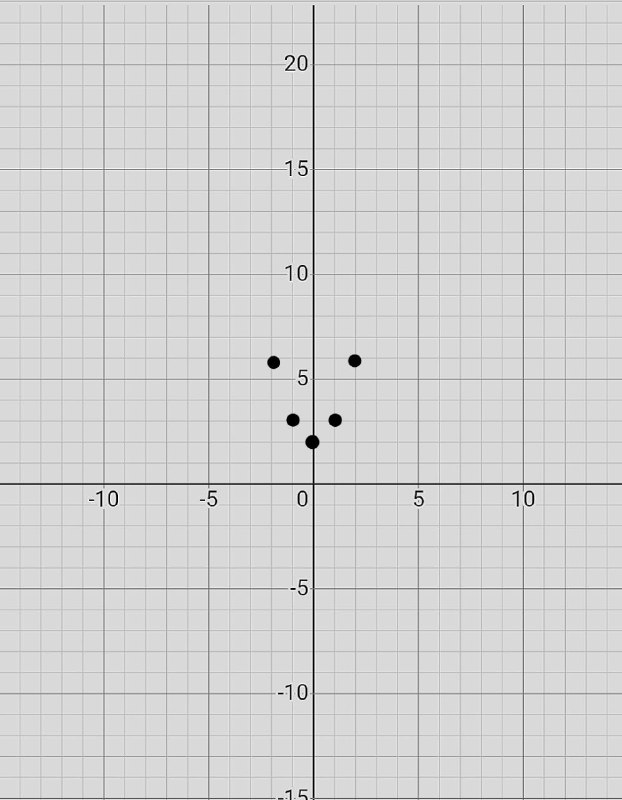
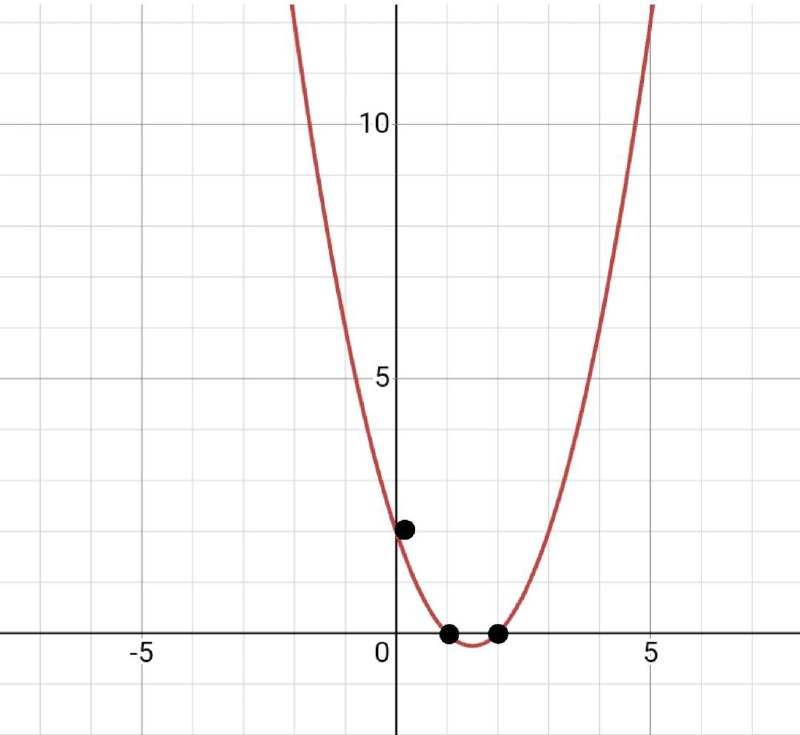
3. Проводим нашу параболу через точки.
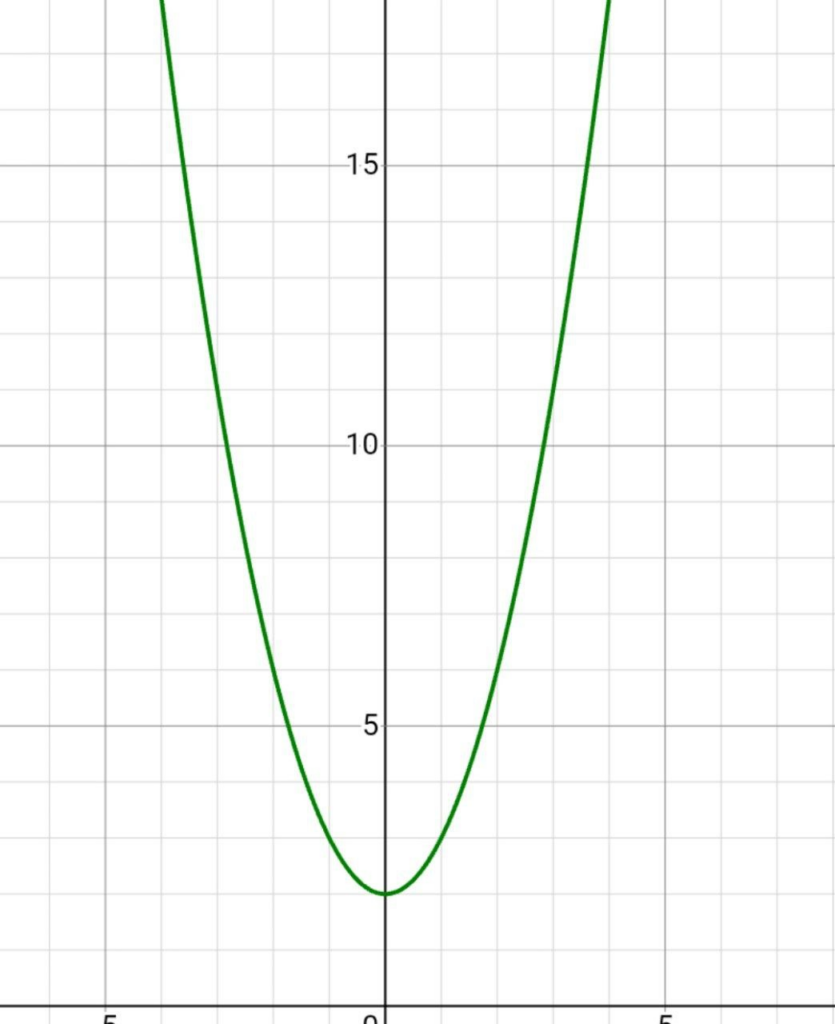
Для закрепления разберем параболу, которая задана уравнением у=х^2+2х-3
1) а=1, значит ветви параболы направлены вверх, а b=2 с=-3.
2) Находим вершину (х0; у0).
х0=-2/2×1=-1
у0=(-1)^2+2×(-1)-3=1-2-3=-4
(-1; -4)
3) Ось симметрии х=-1.
4) Пересечения с осью Оу: с=-3, значит (0, -3).
С осью Ох: х^2+2х-3=0
D=2^2-4×1×(-3)=4+12=16=4^2
х1=-2+4/2×1=2/2=1 (1; 0)
х2=-2-4/2×1=-6/2=-3 (-3; 0)

Кубическая парабола.
Из названия понимаем, что данная функция связана с третьей степенью. Также становится ясно то, что этот особый вид кривой, которая имеет форму чем-то схожей с параболой.

Уравнение кубической функции имеет вид y=ax^3+bx^2+cx+d. Здесь a, b, c, d — тоже являются важными параметрами, влияющими на график. В данной случае это коэффициенты, определяющие форму и положение кривой.
Посмотрев на иллюстрацию понимаем, что визуальное отражение кубической функции напоминает развернутую параболу.

Как мы и говорили, график кубической параболы может иметь различные формы в зависимости от значений коэффициентов a, b, c, d.
От величины а, точнее от знака перед ней зависит направление нашей параболы.
Когда а является положительным числом, то функция направлена вверх, то есть бесконечно возрастает. Потому что если посмотреть то наш график на всей оси абсцисс (х) слева направо «поднимается».
Когда а является отрицательным числом, то функция направлена вниз, то есть бесконечно убывает. Потому что если посмотреть, то наш график на всей оси Ох слева направо «падает».
| а<0 | а>0 |
 | 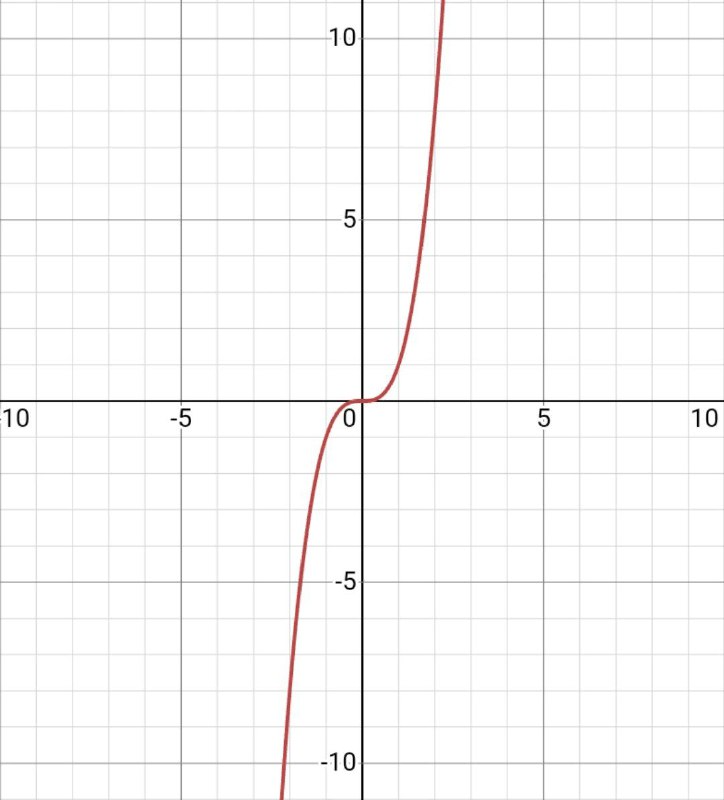 |
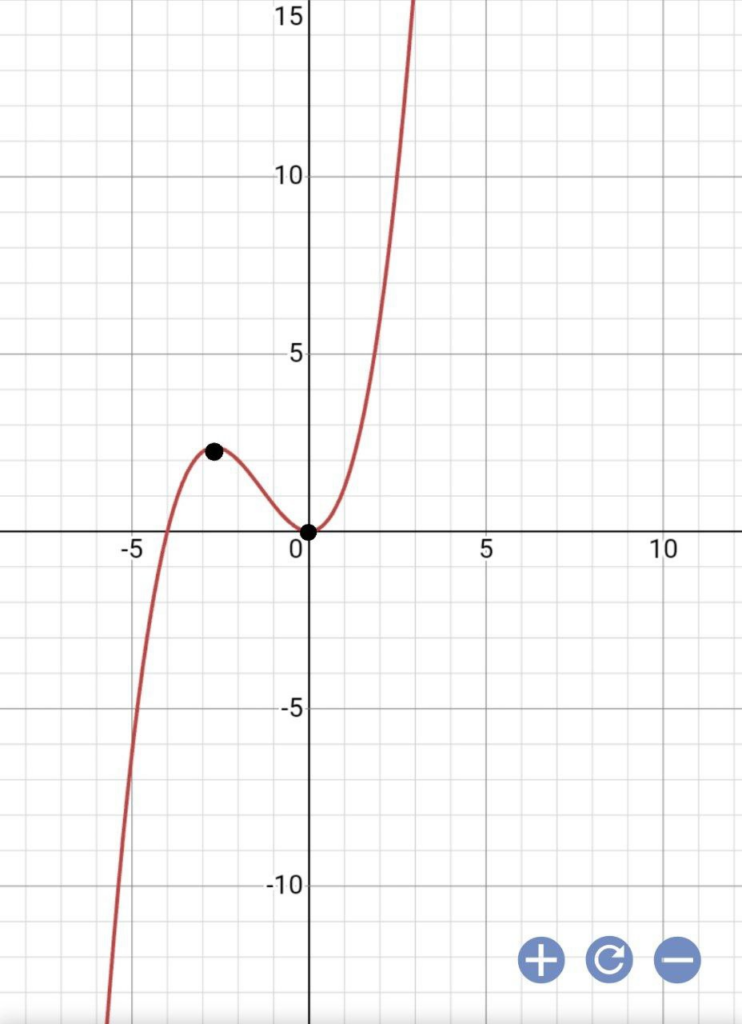
Точки отмеченные на графике называются точками перегиба.
Это места, в которых меняется направление кривизны нашей функции.
Иногда точек перегиба бывает несколько, иногда такая точка одна.
Для того, чтобы найти их координаты, нам необходимо решить такое уравнение: f(x)»=0, где f(x)» является второй производной функции.
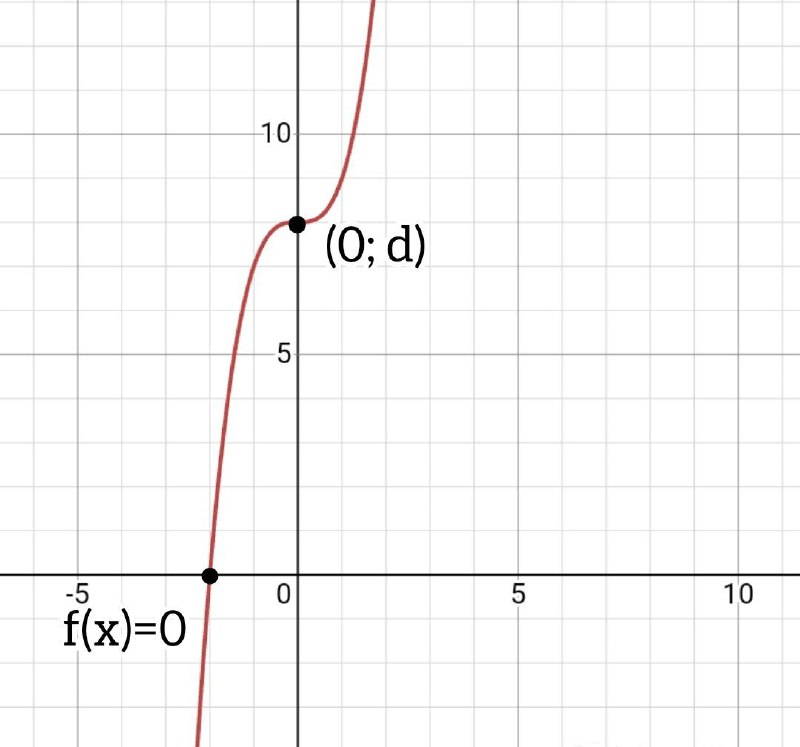
Для нахождения пересечения нашей кривой с осями, нам нужно запомнить пару моментов.
1) Пересечение с осью Ох будет когда f(x)=0.
Пересечение с осью Оу будет в точке (0, d).
Рассмотрим на примере у=х^3-8
1) Ось абсцисс : х^3-8=0
х^3=8
х^3=2^3
х=2
(2;0)
2) Ось ординат (0;-8)
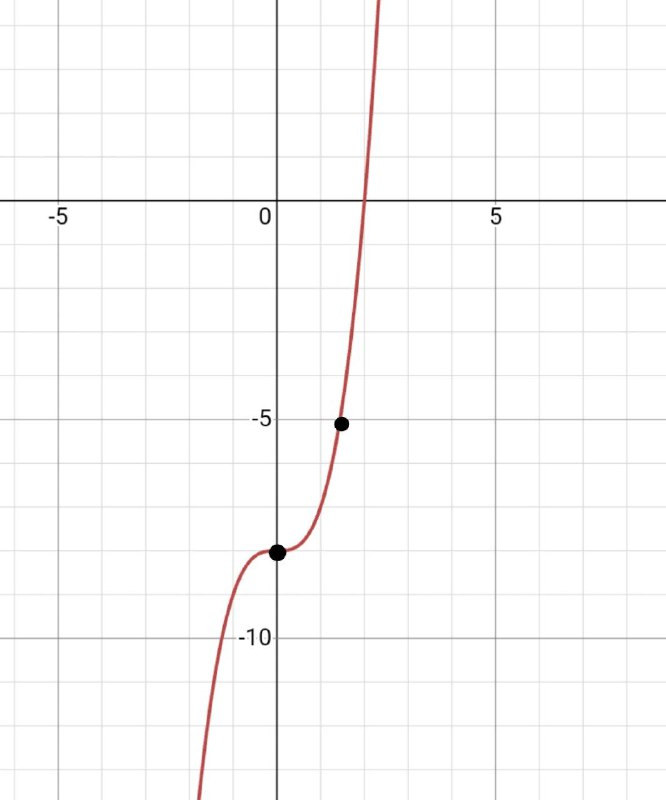
Для того, чтобы построить график можно просто взять 5 точек (-2, -1, 0, 1, 2), подставить их в наш аргумент, сделать таблицу и начертить наш график.
Возьмем функцию f(x)=2x^3+1
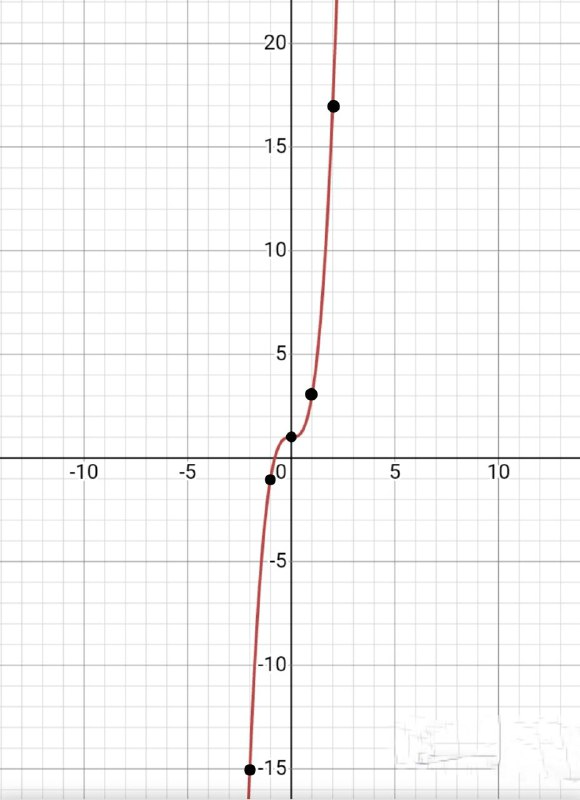
1) При х=-2 у=2×(-2)^3+1=-3 (-2; -15)
2) При х=-1 у=2×(-1)^3+1=-2 (-1; -1)
3) При х=0 у=2×0^3+1=1 (0;1)
4) При х=1 у=2×1^3+1=4 (1;3)
5) При х=2 у=2×2^3+1=5 (2;17)
Расставляем наши точки на координатной оси и чертим график.
Давайте рассмотрим функцию у=х^3+1.
а=4 b=0 c=0 d=4
а>0 , значит кубическая парабола возрастает.
Точка пересечения с Оу: (0;1)
Точка пересечения с Ох: х^3+1=0
х^3=-1
х=-1
(-1; 0)
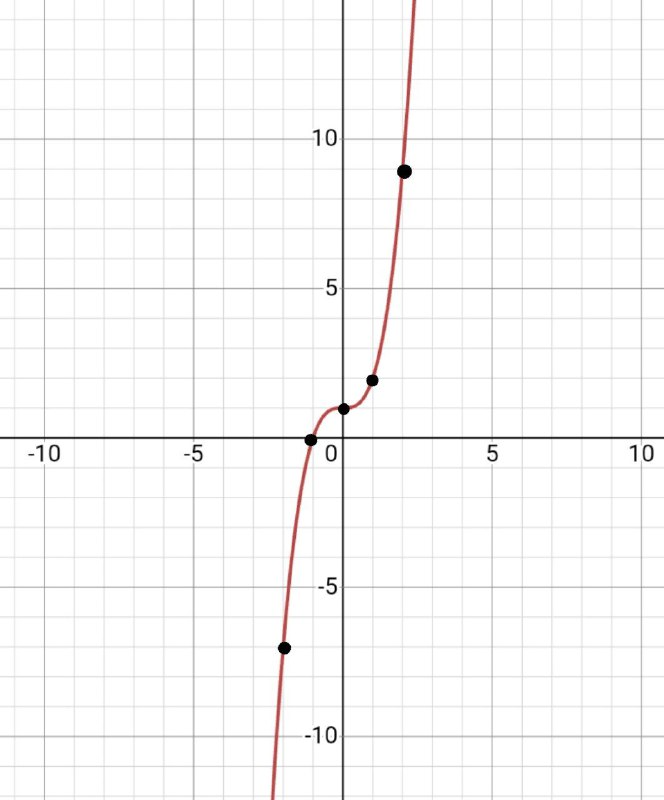
1) При х=-2 у=(-2)^3+1=-7 (-2;-7)
2) При х=-1 у=(-1)^3+1=0 (-1; 0)
3) При х=0 у=0^3+1=1 (0;1)
4) При х=1 у=1^3+1=2 (1;2)
5) При х=2 у=2^3+1=9 (2;9)
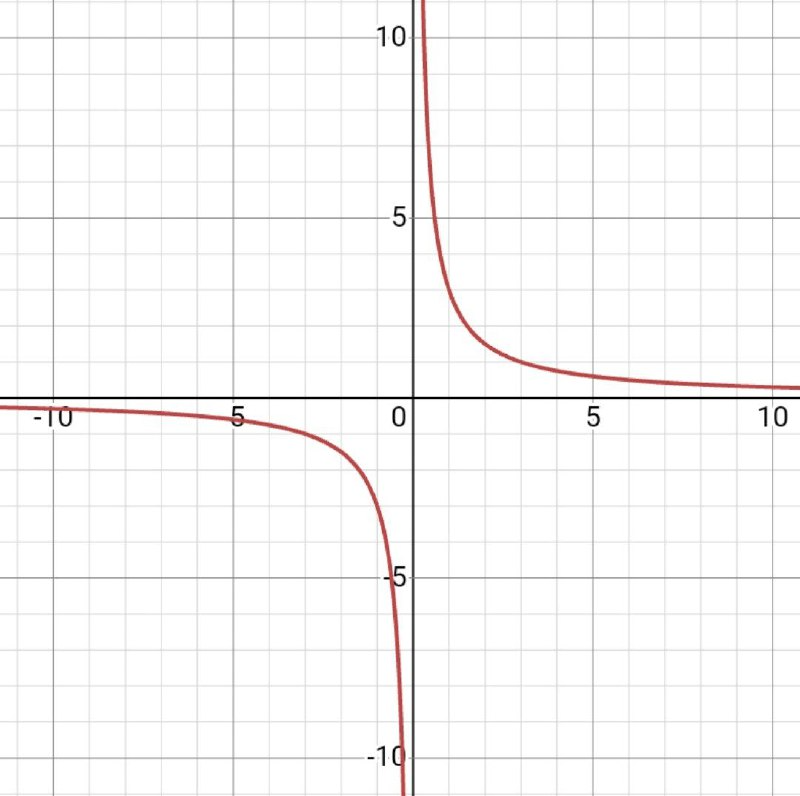
Гипербола.
Функция гипербола имеет следующий вид: f(x) = k/x, где k – постоянное число.
График функции гипербола представляет собой две непересекающиеся ветви, симметричные относительно осей координат.
Наш параметр k определяется в каких 2 четвертях координатной плоскости будут находиться ветви гиперболы.
В случае, когда k больше нуля, то график расположен в I и III четвертях.
Когда k меньше нуля, то график расположен во II и IV четвертях.
| k<0 | k>0 |
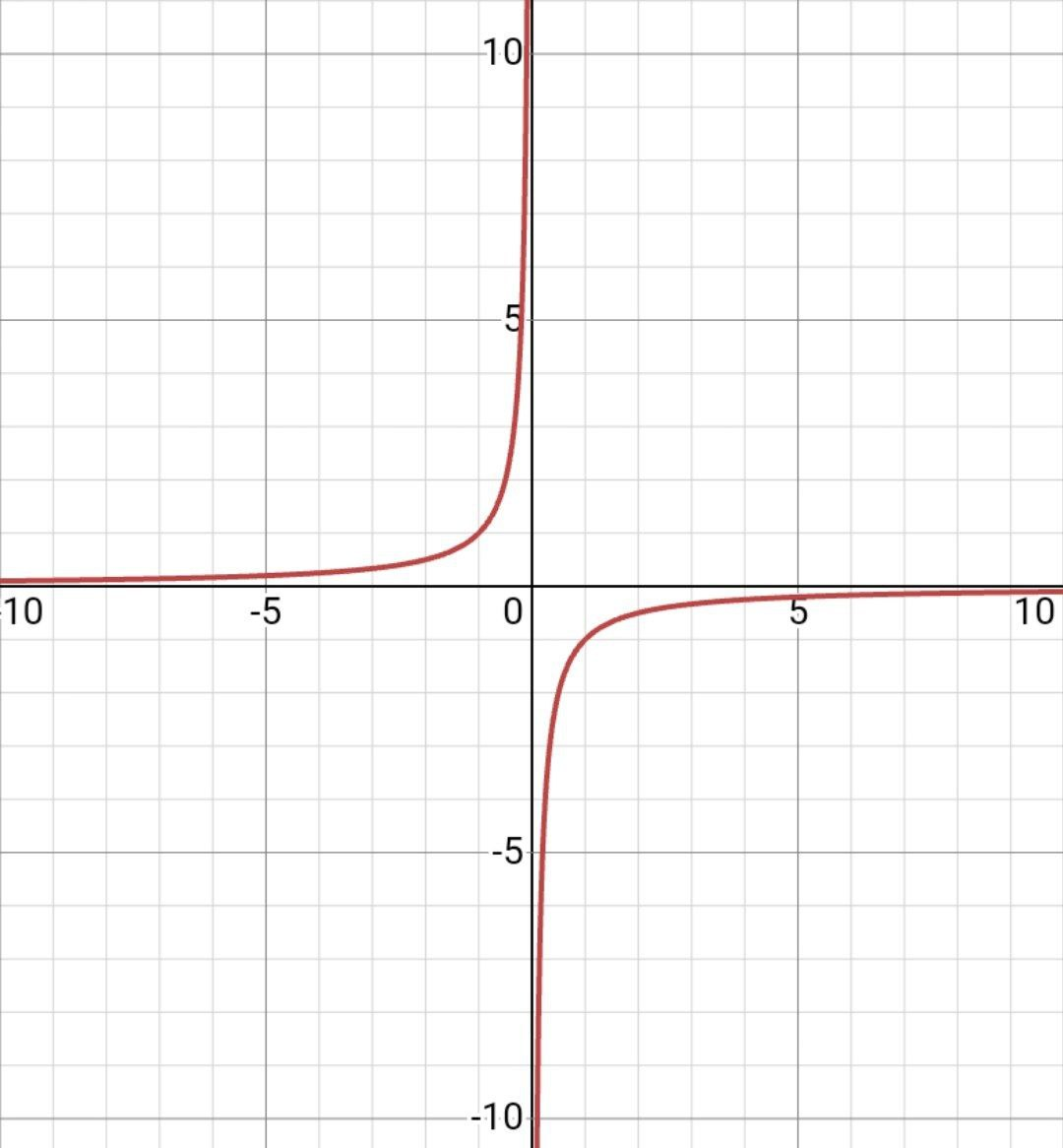 |  |
В стандартном варианте ось ординат и ось абсцисс по отношению к гиперболам являются асимптотами. Простым языком говоря, ветви гиперболы будут стремиться к оси Ох и Оу , но никогда их не достигнут. А это значит, что такой график не пересекает координатные оси ни в каком случае. И отсюда вытекает то, что переменные х и у в данной функции не могут быть равны нулю.
В других случаях, отличных от стандарта графики гипербол тоже можно сдвинуть вверх, вниз, влево или вправо, в зависимости от значений параметров функции. И тогда асимптоты могут быть другими.
Это происходит когда функция задана другим уравнением, которое выглядит так: у=k/(x-a)+b.
В данном случае асимптотами будут прямые х=а и у=b.
Если а является положительным числом, то смещение будет сделано влево.
а=2, значит график уходит на 2 единицы влево.
Если а является отрицательным числом, то смещение будет сделано вправо.
а=-4, тогда гипербола делать 4 “шага” вправо.
Когда b меньше нуля, то асимптота смещается вниз.
b=-3, выходит график опускается на 3 единицы.
Когда b больше нуля, то асимптота смещается вверх.
b=1, получается, что гипербола подниматься на 1 ступеньку.
| а<0 | Стандарт | а>0 |
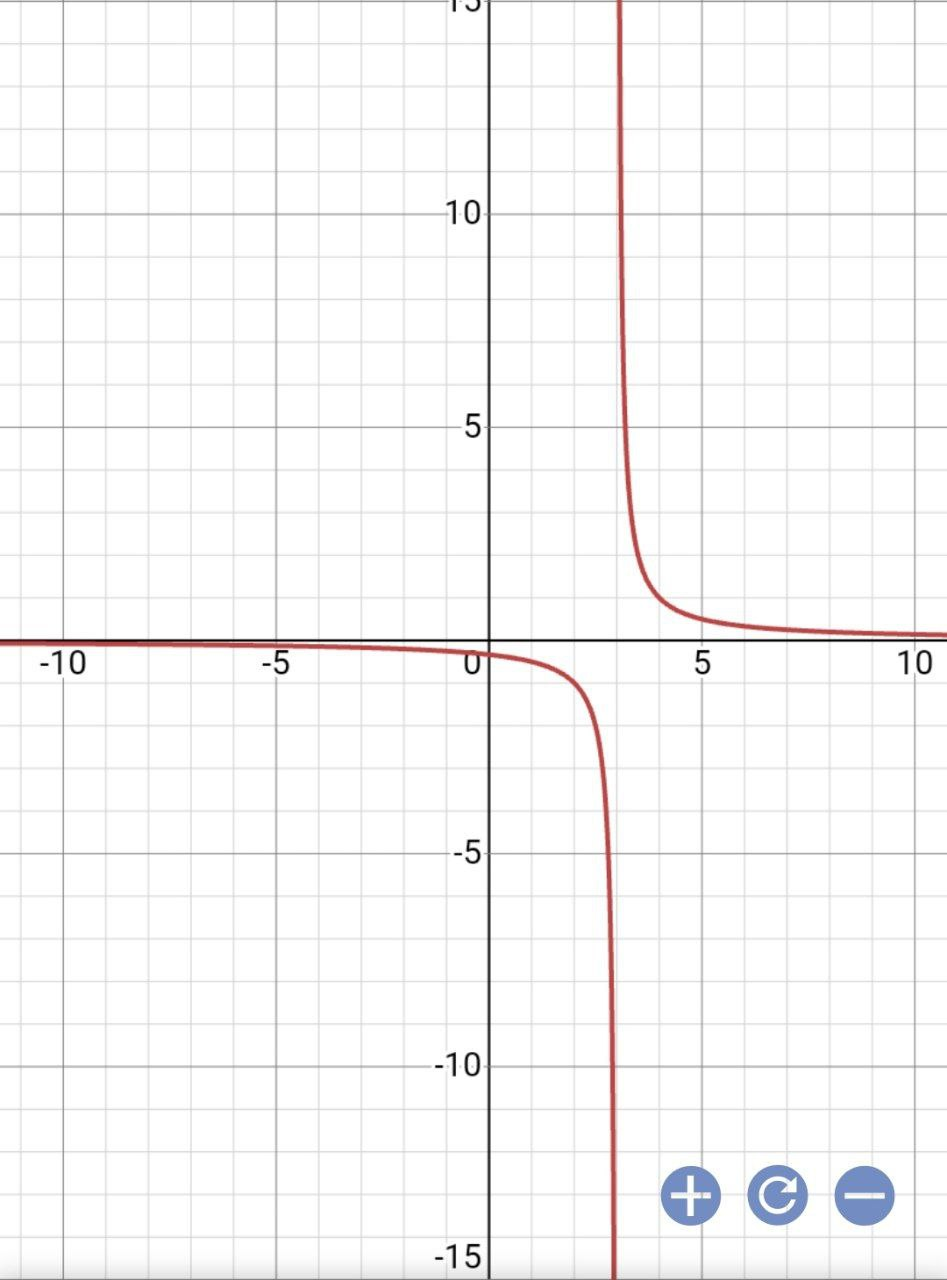 |  | 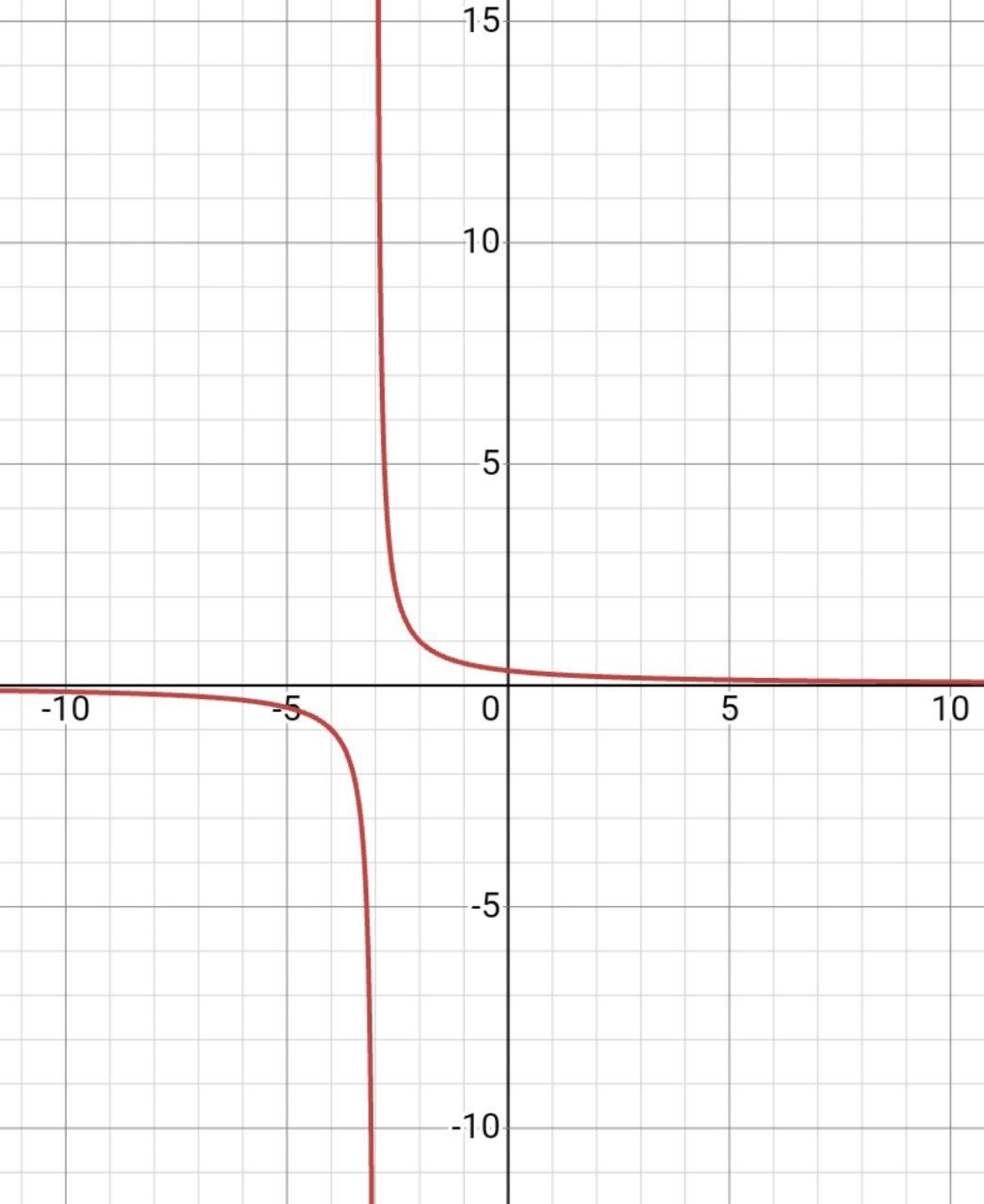 |
| b<0 | Стандарт | b>0 |
 |  | 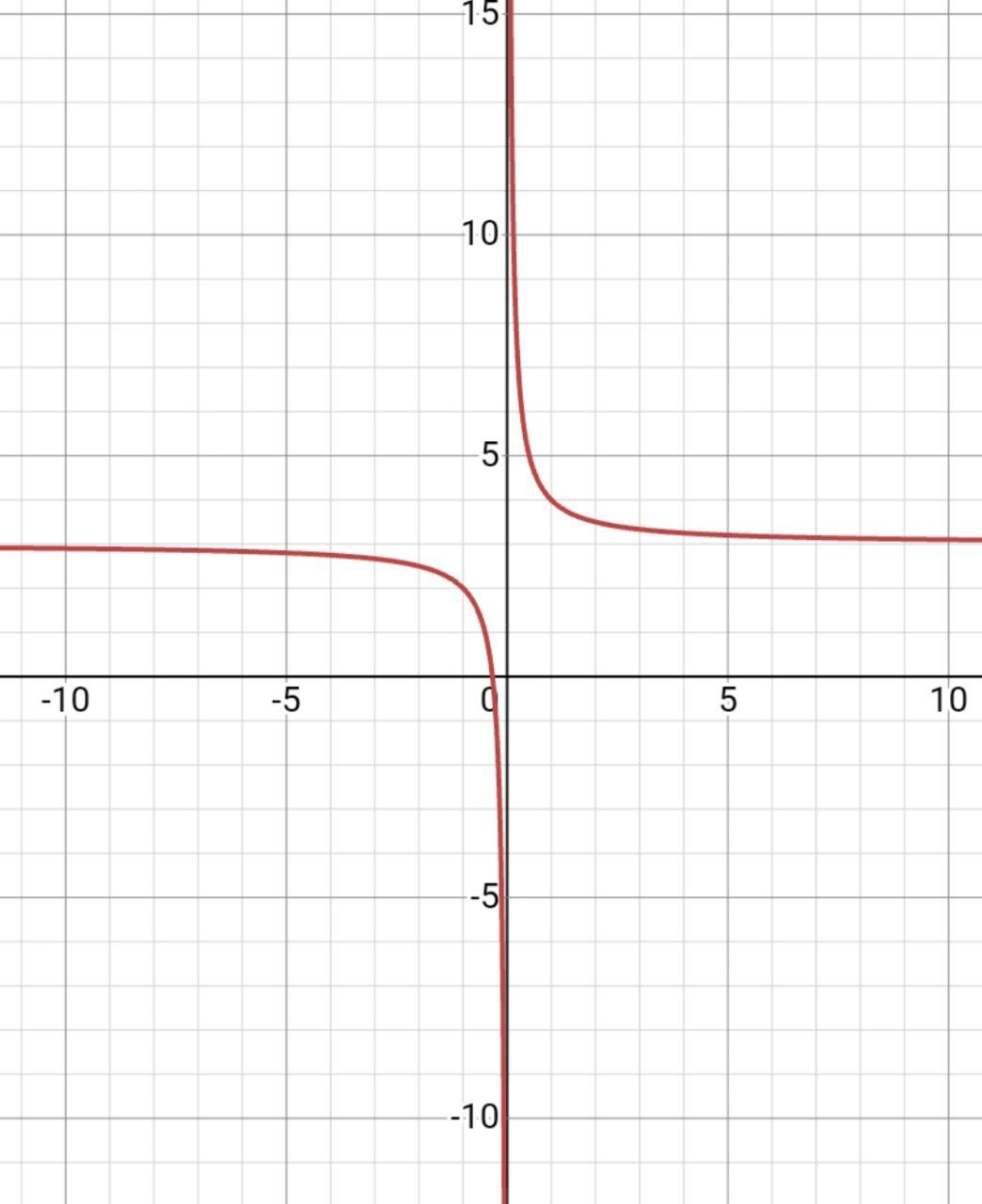 |
Для того, чтобы начертить сам график нам нужно минимум 6 чисел ( 3 положительных и 3 отрицательных).
Рассмотрим на примере у=2/х.
Подставим (-4, -2, -1, 1, 2, 4) вместо х.
1) При х=-4 у=2/(-4)=-0.5
2) При х=-2 у=2/(-2)=-1
3) При х=-1 у=2/(-1)=-2
4) При х=-0.5 у=2/(-0.5)=-4
5) При х=0.5 у=2/0.5=4
6) При х=1 у=2/1=2
7) При х=2 у=2/2=1
8) При х=4 у=2/4=0.5
Составим таблицу.
| х | -4 | -2 | -1 | -0.5 | 0.5 | 1 | 2 | 4 |
| у | -0.5 | -1 | -2 | -4 | 4 | 2 | 1 | 0.5 |
Чертим координатную плоскость, отмечаем наши точки и проводим ветви гиперболы.
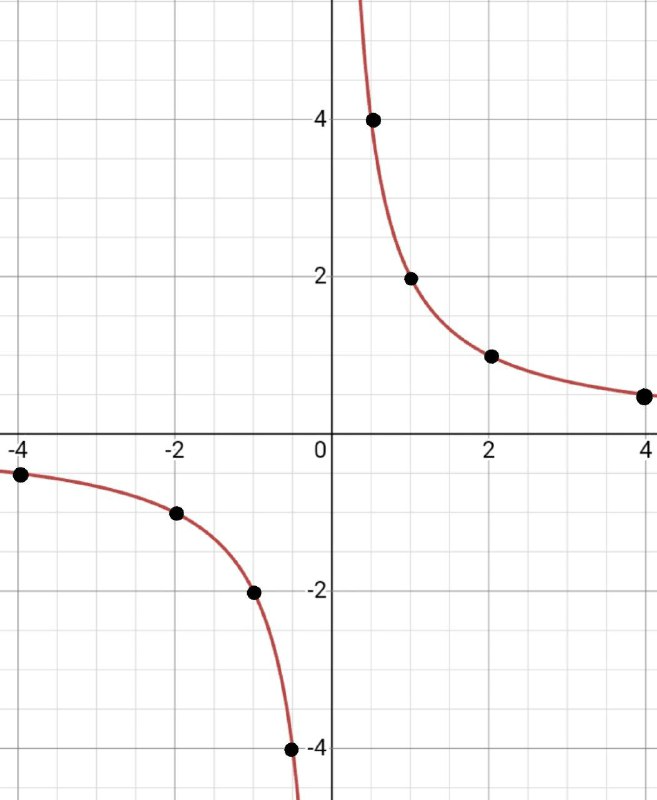
Вот и все наш график готов.
Если вы вдруг себя ощущаете примерно так :
то не стоит отчаиваться, потому что дальше будут представлены несколько таблиц, подсказок и разбор заданий по данной теме для того, чтобы вы не запутались в материале.
Заключительная таблица-шпаргалка.
| Линейная функция. | Парабола. | Кубическая парабола. | Гипербола. |
| f(x)=kx+b. | f(x)=ax^2+bx+c. | f(x)=ax^3+bx^2+cx+d. | f(x) = k/x |
 |  |  |  |
Графики функций, с которыми чаще всего приходиться работать.
Еще необходимо упомянуть, что помимо данных функций еще существуют логарифмические, показательные и тригонометрические функции. Поскольку данные функции и их графики требуют более детального изучения, то они будут рассматриваться в отдельных статьях.
Задания для самопроверки:
Задание 1
Какая технология позволяет виртуальным турам создавать ощущение объема и присутствия?
- Двухмерная графика
- Анимация
- Трехмерное моделирование
- Панорамная съемка
Задание 2
Какое оборудование чаще всего используется для создания 3D панорам?
- Обычные цифровые камеры
- Сверхширокоугольные камеры
- 360-градусные камеры
- Видеокамеры
Задание 3
Что является преимуществом виртуальных туров?
- Невозможность использования интерактивных элементов
- Высокие технические требования
- Удобство и доступность в любое время и из любой точки мира
- Ограниченная детализация изображений
Ответы: 1 – 4; 2 – 3; 3 – 3.

 4,14/5
4,14/5