Идеальный газ: МКТ, уравнение Клапейрона-Менделеева, изопроцессы, закон Дальтона и температура
Введение
По новому плану ЕНТ по физике, введенному в использование с 2024 года, на экзамене абитуриентам обязательно встретятся 7 вопросов по молекулярной физике и тепловым явлениям. Идеальный газ считается основой программы и его знание необходимо для успешного прохождения испытания. Он закладывает фундамент для дальнейшего изучения термодинамики, химии и других естественнонаучных дисциплин.
Сегодня вы узнаете:
- Что такое идеальный газ?
- Какие уравнения описывают идеальный газ?
- Какой физический смысл у температуры?
- Что такое изопроцессы и зачем они нужны?
- Как найти давление смеси газов?
Идеальный газ
Как вы уже знаете МКТ основывается на трех фундаментальных положениях:
- Все тела состоят из атомов и молекул.
- Эти частицы находятся в непрерывном хаотичном движении (броуновское движение).
- Частицы взаимодействуют друг с другом и их взаимодействия подчиняются законам механики.
Понимая, что все, в том числе и газы состоят из таких мельчайших частиц, мы можем разделить физические величины, описывающие газ на два типа: макроскопические и микроскопические. Как следует из названий, такие индивидуальные характеристики, как скорость и масса молекул относятся к микроскопическим, а объём, давление и температура к макроскопическим, потому что они не требуют рассмотрения более детальной картины. МКТ же полагаясь на свои положения дает нам связь между этими типами величин с помощью модели идеального газа. Идеальный газ – это гипотетический газ, молекулы которого не взаимодействуют друг с другом (нет сил притяжения) и сталкиваются абсолютно упруго. Хоть такой газ и не существует в природе, модель является отличным приближением для реальных газов при достаточно высоких температурах и низких давлениях и позволяет упростить формулы и вычисления в разы!


Основное уравнение МКТ
Давайте познакомимся с основным уравнением МКТ, вывод которого для ЕНТ вам не нужен, но знание и понимание, которого просто необходимо:
p = 1/3nmv^2, (v должна быть с черточкой сверху)
где p — давление идеального газа, n — концентрация, v — средняя скорость и m — масса молекулы. n это количество молекул, находящихся в данном объёме вещества N/V. Как можно наблюдать, макроскопический параметр, как давление, связан с микроскопическими скоростью и массой молекул!
Пример 1. Найдите концентрацию газа, если давление равно 10 кПа, средняя скорость частиц = 450 м/с, а масса молекулы равна 5*10^-26 кг.
n = 3p/mv^2 = 3*10000/(5*10^-26*450^2) = 2.96*10^24 м^-3.
Сверху, уравнение записано в основном своем виде, но у нас также есть и другие формы записи:
2) Каждая молекула газа хаотично движется и имеет некую скорость. Значит она имеет… КИНЕТИЧЕСКУЮ энергию! E = mv^2/2 (энергия и скорость с черточками). Тогда, 2E = mv^2 => p = 2/3nE (энергия с черточкой). Другая популярная и удобная форма записи. Давление равно двум третьим произведения концентрации идеального газа на величину средней кинетической энергии молекул газа.
3) Выразим плотность вещества через произведения массы одной частицы на их количество поделенное на данный объем. Концентрация это отношения количества частиц в данном объеме, поэтому получим следующее выражение: rho = Nm/V = nm. Заменяя в p = 1/3nmv^2, получим p = 1/3rho v^2.
Пример 2. Найдите давление газа, если его плотность равна 520 кг/м3, а скорость молекул 440 м/с.
p = 1/3rho v^2 = ⅓ * 520 * 440^2 = 76267 Па
Температура
Теперь настало время поговорить про температуру. Все мы знаем, что это за величина. Термометры имеют разные шкалы измерений. Допустим по Цельсию мы имеем реперную точку — температура таяния льда (0 градусов по Цельсию). 100 градусов это уже температура кипения воды. В термодинамике и МКТ, вместо шкалы Цельсия используется шкала Кельвина:
Температура в Кельвинах = Температура в Цельсиях + 273
При решении задач всегда необходимо переводить градусы в Кельвины, иначе вы получите неверное значение, что не должно быть вашей ошибкой на ЕНТ!
Запомните, в природе не бывает температуры меньше нуля Кельвинов. Это так называемый абсолютный ноль при котором частицы “прекращают” свое движение. Почему “прекращают” в скобках вы поймете позже при изучении квантовой физики уже на школьном уровне, а пока в рамках данного раздела примем “прекращают” за прекращают.
Мы разобрались, что бывают разные шкалы измерений, что такое абсолютный ноль и определили, что необходимо переводить значения температуры в Кельвины, но какой же все таки физический смысл у температуры?
Опытным путем была выведена некая формула, которая отражает линейную зависимость давления любого газа от температуры. Подставляя эту формулу давления в p = 2/3nE (энергия с черточкой) было найдено уравнение средней кинетической энергии молекул (нам нужно именно это выражение): E = 3/2kT (Е с черточкой), где коэффициент k — постоянная Больцмана, равная 1.38 * 10^-23 Дж * К^-1.
Что для нас означает выражение E = 3/2kT (Е с черточкой)? Температура это мера средней кинетической энергии молекул. Логично, чем больше температура, тем больше скорость молекул, а чем она меньше, тем меньше и скорость (теперь можно понять и логику “абсолютного нуля”).
Подставим Е в p = 2/3nE: p = nkT.
Давление газа прямо пропорционально его температуре и концентрации молекул газа.
Пример 3. Концентрация газа равна 2.7*10^25 м^-3. Найдите давление газа, если его температура равна 350 К.
p = nkT = 2.7*10^25 * 1.38 * 10^-23 * 350 = 130410 Па
Также давайте покажем знаменитую формулу “3 кота на мясо”:
E = mv^2/2, также E = 3/2kT.
Тогда, mv^2/2 = 3/2kT
v = sqrt{3kT/m}
(скорость с черточкой, это среднеквадратичная скорость)

Уравнение состояния или же уравнение Клапейрона-Менделеева:
Как вы уже могли заметить данная статья содержит огромное количество учебного материала в виде формул. Однако, эти формулы выводятся из друга и взаимосвязаны. Тоже самое касается уравнения состояния, которым будут решаться большинство задач ЕНТ по термодинамике.
Из прошлого параграфа возьмем p = nkT, где концентрация n = N/V = nu * Na/V, а Na — число Авогадро, равное 6.02 * 10^23 моль-1. Тогда p = nu * Na * k * T/V => pV = nu * Na * k * T. Независимо друг от друга Клапейрон и Менделеев вывели новую формулу, а именно уравнение состояния:
pV = nu * R* T
где R = Na * k это универсальная газовая постоянная, равная 8.31 Дж/мольК. НЮАНС: сегодня во многих учебниках и также во многих системах образования n это не концентрация газа, а именно наше количество вещества nu, поэтому вы можете встретить pV = n * R* T, что будет иметь тот же самый смысл. Концентрацию газа же зачастую обозначают буквой c! Количество вещества как мы помним это отношение массы газа к его молярной массе, измеряемое в [моль].
Закон Дальтона
Представим, что мы имеем некую смесь газов. Как определить давление газа, ведь мы точно не знаем какая у него будет молярная масса и другие параметры. На помощь приходит он! Закон Дальтона гласит, что в любой смеси газов общее давление будет равно сумме парциальных давлений всех газов:
p = p1 + p2 + p3 + … + pn
Парциальное давление — это давление, которое теоретически имел бы наш газ, если бы находился в данном объеме не в смеси.
Состояние газа — это совокупность его параметров, которые определяют его физическое состояние в данный момент времени. Основными параметрами, характеризующими состояние газа, являются: давление p, объем V, температура T. Мы можем менять состояние газа (значения характеристик газа), переводя его из одного в другое (из одних значений параметров в другие). Зная уравнение Клапейрона-Менделеева, мы можем рассмотреть различные случаи при которых один параметр остается постоянным, называемые изопроцессами.
Изопроцессы
Закон Бойля-Мариотта (изотермический процесс)
Закон Бойля-Мариотта утверждает, что для данного количества газа при постоянной температуре произведение давления на объем остается постоянным:
pV = const
p1V1=p2V2
Закон Гей-Люссака (изобарический процесс)
Закон Гей-Люссака утверждает, что при постоянном давлении объем газа пропорционален его абсолютной температуре:
V/T = const
V1/T1=V2/T2
Закон Шарля (изохорический процесс)
Закон Шарля утверждает, что при постоянном объеме давление газа пропорционально его абсолютной температуре:
p/T = const
p1/T1=p2/T2
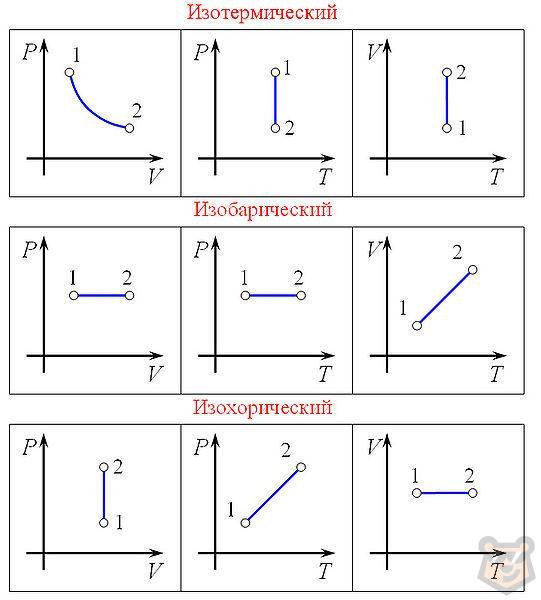
Комментарий. Нужно будет под каждым изопроцессом добавить по три соответствующих графика.
Пример 4. Идеальный газ занимает объем 10 литров при давлении 2 атмосферы и температуре 300 К. Рассчитайте объем газа при тех же условиях, но при давлении 4 атмосферы.
Обязательно переводим литры в метры кубические, а атмосферы в паскаль:
10 литров = 10 * 10^-3 м3
2 атм = 2 * 10^5 Па
4 атм = 4 * 10^5 Па
Используем закон Бойля-Мариотта (так как температура по условию постоянна): p1V1=p2V2
V2 = p1V1/p2 = 2 * 10^5 * 10 * 10^-3/4 * 10^5 = 5 * 10^-3 м3 = 5 литров!
Можете заметить, что ответ вышел бы такой же, если бы мы не переводили никакие единицы, однако это правильно и поможет выработать правильные привычки решения задач для ЕНТ.
Фактчек
- Модель идеального газа, основываясь на положениях МКТ, позволяет упростить сложные системы и дает возможность исследовать фундаментальные законы, регулирующие поведение газов. Идеальный газ описывается основным уравнением МКТ, которое может принимать разные формы (p = 1/3nmv^2, p = 2/3nE, p = 1/3rho v^2), а также уравнением состояния pV = nu RT, которое также называют уравнением Клапейрона-Менделеева.
- Мы познакомились с универсальной газовой постоянной R и постоянной Больцмана k.
- Закон Дальтона гласит, что сумма всех парциальных давлений в смеси газов будет равна общему давлению этой смеси.
- Когда мы меняем параметры газа, как давление, объем и температура, мы меняем его состояние.
- Когда один параметр остается постоянным, мы называем его изопроцессом. Существует три закона, описывающих изопроцессы: Шарля, Гей-Люссака и Бойля-Мариотта. Каждый процесс можно изобразить на графике. Графики будут отличаться в зависимости от того какую диаграмму зависимости мы примем: pV, pT или же VT.
Задания для самопроверки:
Задание 1
Идеальный газ имеет объем 10 литров при температуре 300 К. Какой объем он займет при температуре 450 К, если давление остается постоянным?
A) 25 литров
B) 15 литров
C) 5 литров
D) 30 литров
E) 15.5 литров
Задание 2
Идеальный газ содержит 2*10^23 молекул, каждая из которых имеет среднеквадратичную скорость 500 м/с. Объем сосуда составляет 0.1м^3. Рассчитайте давление газа, если масса молекулы 5.7 * 10^-26 кг:
A) 17800 Па
B) 11400 Па
C) 9500 Па
D) 7777 Па
E) 19670 Па
Задание 3
Средняя кинетическая энергия одной молекулы газа при температуре 300 К
A) 2.9 * 10^-16
B) 1.7 * 10^-5
C) 8.4 * 10^-19
D) 6.21 * 10^-21
E) 7.2 * 10^-24
Ответы:
1 — B
2 — C
3 — D

